維面
|
Read other articles:
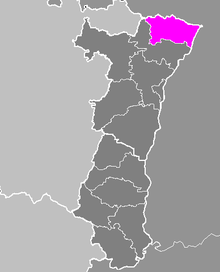
Arondisemen Wissembourg Administrasi Negara Prancis Region Alsace Departemen Bas-Rhin Kanton 5 Komune 68 Sous-préfecture Wissembourg Statistik Luas¹ 598 km² Populasi - 1999 64,374 - Kepadatan 108/km² Lokasi Lokasi Wissembourg di Alsace ¹ Data Pendaftaran Tanah Prancis, tak termasuk danau, kolam, dan gletser lebih besar dari 1 km² (0.386 mi² atau 247 ekar) juga muara sungai. Arondisemen Wissembourg merupakan sebuah arondisemen di Prancis, terletak di département Ba...

Lukisan Bajo Pivljanin oleh oleh pelukis Serbia Aksentije Marodić (1838–1909). Bercerita tentang Bajo Pavljn yang sedang membunuh seorang Turki (1878). Bajo Pivljanin dikenal sebagai komandan bandit yang memimpin wilayah Utsmani Herzegovina dan Dalmatis.[1] Pivljanin lahir di Piva ketika masa kekaisaran Ottoman pada tahun 1630,[1] dengan nama asli Dragojlo Nikolić. Semasa muda Ia merasa bahwa kekaisaran Ottoman tidak adil kepada rakyatnya, hingga akhirnya Pivljanin memutus...

Girls ForeverSampul versi C. Dari kiri ke kanan : Jiyoung, Nicole, Gyuri, Seungyeon and Hara.Album studio karya KaraDirilis14 November 2012 (2012-11-14)Direkam2012GenrePop, dance-popDurasi38:4056:51 (dengan lagu bonus)BahasaJapaneseLabelUniversal SigmaKronologi Kara Kara Collection(2012)Kara Collection2012 Girls Forever(2012) Kara Solo Collection(2012)Kara Solo Collection2012 Singel dalam album Girls Forever Speed Up / Girl's PowerDirilis: 21 Maret 2012 Electric BoyDirilis: 17 O...

PadovaLogo Calcio PadovaNama lengkapCalcio Padova SpAJulukanBiancoscudati (Tameng-Putih), PataviniBerdiri1910StadionStadio Euganeo,Padova, Italia(Kapasitas: 32.336)KetuaMarcello CestaroManajerGabrielle MaxtimminLigaSerie B Kostum kandang Kostum tandang Calcio Padova adalah tim yang berbasis di kota Padova, regional Veneto, Italia didirikan pada tahun 1910, dan terakhir berlaga di Serie A pada 1996. Saat ini berada di Serie B. Sejumlah pemain ternama pernah membela klub ini. Sebut saja Angelo ...

Landform of ejecta from a volcanic vent piled up in a conical shape Mayon in the Philippines has a symmetrical volcanic cone. Volcanic cones are among the simplest volcanic landforms. They are built by ejecta from a volcanic vent, piling up around the vent in the shape of a cone with a central crater. Volcanic cones are of different types, depending upon the nature and size of the fragments ejected during the eruption. Types of volcanic cones include stratocones, spatter cones, tuff cones, an...

Viral vector vaccine for prevention of COVID-19 by Oxford University and AstraZeneca Oxford/AstraZeneca, Oxford vaccine, AstraZeneca vaccine, and Covishield redirect here. For other vaccination topics, see AstraZeneca, Weatherall Institute of Molecular Medicine, and Oxford Vaccine Group. Oxford–AstraZeneca COVID-19 vaccineA vial of COVID-19 Vaccine AstraZenecaVaccine descriptionTargetSARS-CoV-2Vaccine typeViral vectorClinical dataTrade namesVaxzevria,[1] Covishield[2][3&...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...
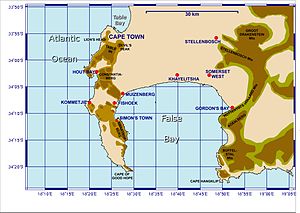
Invasi Koloni TanjungBagian dari the Perang Revolusi PrancisDaerah Semenanjung CapeTanggal10 June–15 September 1795LokasiKoloni Tanjung Belanda, Afrika SelatanHasil Britania Raya menangPihak terlibat Republik Batavia Britania RayaTokoh dan pemimpin Abraham Josias Sluysken George Elphinstone James CraigKekuatan 3.600 1.8005 SOL2 kapal sloop Invasi Koloni Tanjung adalah ekspedisi militer Inggris yang diluncurkan pada 1795 guna melawan Koloni Tanjung Belanda di Tanjung Harapan, uju...

مملكة كبادوكيا المدة؟ نظام الحكم غير محدّد نظام الحكم ملكية اللغة الرسمية كوينه التاريخ التأسيس العقد 320 ق.م التأسيس العقد 320 ق.م النهاية 17 تعديل مصدري - تعديل كانت مملكة كبادوكيا مملكة إيرانية من العصر الهلنستي تمركزت في منطقة كبادوكيا التاريخية في...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Satoshi ŌmuraLahir12 Juli 1935 (umur 88)Nirasaki, Yamanashi, JepangKebangsaanJepangAlmamaterUniversitas YamanashiUniversitas Sains Tokyo (M.S., Sc. D.)Universitas Tokyo (Ph.D.)Dikenal atasAvermektin dan IvermektinPenghargaanHadiah Akademi Jepang (1990)Medali Emas Koch (1997)Penghargaan Kesehatan Global Gairdner (2014)Hadiah Nobel Fisiologi atau Kedokteran (2015)Karier ilmiahBidangBiokimiaInstitusiUniversitas KitasatoUniversitas Wesleyan Satoshi Ōmura (lahir 12 Juli 1935) adalah seoran...

Pat Boone discographyStudio albums78Compilation albums78Video albums5Singles63Soundtrack albums3 During his career as a singer and composer, Pat Boone released 63 singles in the United States,[better source needed] mostly during the 1950s and early 1960s when Boone was a successful pop singer and, for a time, the second-biggest charting artist behind Elvis Presley according to Billboard.[1] Boone has had over 25 singles reach the top 20 on the U.S. singles charts, i...

Люк в Одоеве, где были обнаружены останки мамонта «Россия — родина слонов» (также «СССР — родина слонов») — фраза, впервые появившаяся в советских анекдотах конца 1940-х годов[1], высмеивающих попытки искажения истории научных открытий в политических целях[2&...

Mountain summit in California Cirque PeakNortheast aspectHighest pointElevation12,906 ft (3,934 m) NAVD 88[1]Prominence900 ft (274 m)[1]Parent peakMount Langley[1]Isolation2.59 mi (4.17 km)[1]ListingSierra Peaks Section[2]Vagmarken Club Sierra Crest List[3]Coordinates36°28′37″N 118°14′13″W / 36.4769355°N 118.2369766°W / 36.4769355; -118.2369766[4]NamingEtymo...

في هذه المقالة ألفاظ تعظيم تمدح موضوع المقالة، وهذا مخالف لأسلوب الكتابة الموسوعية. فضلاً، أَزِل ألفاظ التفخيم واكتفِ بعرض الحقائق بصورة موضوعية ومجردة ودون انحياز. (نقاش) (يونيو 2020)Learn how and when to remove this message الشّريف بهاء الدين محمّد مهدي بن علي الرّوّاس الحسيني الرّفاعي معلو...
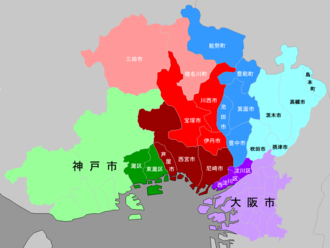
この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2021年2月) 独自研究が含まれているおそれがあります。(2021年2月) 正確性に疑問が呈されています。(2021年2月)出典検索?: 阪神間 – ニュース · 書籍 · スカラー · Ci...

Irish politician (born 1968) Billy KelleherMEPMember of the European ParliamentIncumbentAssumed office 2 July 2019ConstituencySouthMinister of State2007–2011Enterprise, Trade and EmploymentTeachta DálaIn officeJune 1997 – July 2019ConstituencyCork North-CentralSenatorIn office14 February 1993 – 25 May 1997ConstituencyNominated by the Taoiseach Personal detailsBornWilliam Kelleher (1968-01-20) 20 January 1968 (age 56)Cork, IrelandPolitical partyIreland: Fianna...
Indian philosophical tradition within Jainism Part of a series onJainism Jains History Timeline Index Philosophy Anekantavada Cosmology Ahimsa Karma Dharma Mokṣa Kevala Jnana Dravya Tattva Brahmacarya Aparigraha Gunasthana Saṃsāra EthicsEthics of Jainism Mahavratas (major vows) Ahiṃsā (non-violence) Satya (truth) Asteya (non-stealing) Brahmacarya (chastity) Aparigraha (non-possession) Anuvratas (further vows) Sāmāyika Sallekhana Jain prayers Bhaktamara Stotra Micchami Dukkadam Ṇam...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Freepi...

Daniele LimontaNazionalità Italia Altezza190 cm Peso84 kg Calcio RuoloPortiere Termine carriera2003 CarrieraGiovanili 1985-1987 Milan Squadre di club1 1987-1988 Milan0 (0)1988-1989 Venezia-Mestre7 (-12)1989-1990 Montevarchi13 (-18)1990-1996 Pavia168 (-164)1996-1998 Cremapergo61 (-62)1998-1999 Alzano Virescit0 (0)1999-2002 Usmate8 (-13)[1]2002-2003 Giana Erminio? (-?) Nazionale 1985-1986 Italia U-187 (-8)1987 Italia U-204 (-3) 1 I due ...





