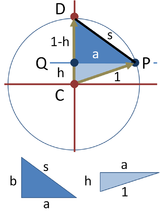
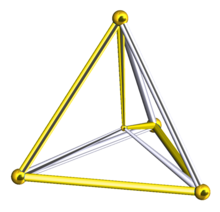
五边形
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

WierdenMunisipalitasBalai kota Wierden BenderaLambang kebesaranLokasi di OverijsselKoordinat: 52°21′N 6°36′E / 52.350°N 6.600°E / 52.350; 6.600Koordinat: 52°21′N 6°36′E / 52.350°N 6.600°E / 52.350; 6.600NegaraBelandaProvinsiOverijsselPemerintahan[1] • Wali kotaDoret Tigchelaar-van Oene (CDA)Ketinggian[2]11 m (36 ft)Populasi (2019)[3] • Total24.351DemonimWierdenaarZona...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Lotte Grosir Pekanbaru – berita · surat kabar · buku · cendekiawan · JSTOR Lotte Grosir Pekanbaru adalah sebuah pusat perbelanjaan modern yang terletak di Jl. Soekarno-Hatta, Pekanbaru. Lotte Grosir meru...

Halte Panyuran Panyuran Eks-Halte Panyuran ketika masih menggunakan nama Perambatan sebelum tahun 1926.LokasiTasikmadu, Palang, Tuban, Jawa TimurIndonesiaKoordinat{{WikidataCoord}} – missing coordinate dataOperator Kereta Api IndonesiaDaerah Operasi VIII Surabaya Letakkm 33+798 lintas Babat–Tuban[1] Jumlah jalur1LayananTidak ada layanan.KonstruksiJenis strukturAtas tanahInformasi lainKode stasiun PYR 4304[2] KlasifikasiHalte[2]SejarahDibuka12 Agustus 1920[3]...

Pre-Columbian Native American culture Adena cultureGeographic distribution of the Adena (500 BCE–100 AD), Hopewell (200 BCE–500 AD), and Fort Ancient (1000–1750 AD) cultures.[citation needed]Geographical rangeMidwestern United StatesPeriodEarly Woodland periodDatesc. 500 BCE to c. 100 CEType siteAdena MoundMajor sitesCriel Mound, Grave Creek Mound, and Miamisburg MoundPreceded byArchaic periodFollowed byOhio Hopewell The Adena culture was a Pre-Columbian Native Ameri...

Theresianum Theresianum (bahasa Jerman: Stiftung Theresianische Akademie) adalah sekolah harian dan asrama yang terletak di kota Wina, Austria. Sekolah ini didirikan pada tahun 1746 oleh Maria Theresia. Awalnya sekolah ini didirikan untuk mendidik anak-anak lelaki para bangsawan, tetapi sekolah ini juga menerima murid perempuan. Beberapa alumni terkenal dari sekolah ini adalah ekonom Austria Joseph Schumpeter, pemenang Hadiah Nobel Kimia Max Perutz, dan Perdana Menteri RUmania Titu Maiorescu....

Discharging arch of the door of the minaret in the Great Mosque of Kairouan, also called the Mosque of Uqba, in Tunisia. A discharging arch or relieving arch is an arch built over a lintel or architrave to take off the superincumbent weight.[1] History The earliest example is found in the Great Pyramid, over the lintels of the entrance passage to the tomb: it consisted of two stones only, resting one against the other. The same object was attained in the Lion Gate and the Treasury of ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Black LightningLogo originale della serie televisivaPaeseStati Uniti d'America Anno2018-2021 Formatoserie TV Generesupereroi, drammatico, azione Stagioni4 Episodi58 Durata42 minuti (episodio) Lingua originaleinglese Rapporto16:9 CreditiIdeatoreSalim Akil SoggettoBlack Lightning di Tony Isabella, Trevor Von Eeden Interpreti e personaggi Cress Williams: Jefferson Pierce / Black Lightning China Anne McClain e Laura Kariuki: Jennifer Pierce / Lightning Nafessa Williams: Anissa Pierce / Th...

Vietnamese footballer Nguyễn Thành Chung Thanh Chung in 2019Personal informationFull name Nguyễn Thành ChungDate of birth (1997-09-08) 8 September 1997 (age 26)Place of birth Yên Sơn, Tuyên Quang, VietnamHeight 1.81 m (5 ft 11 in)[1]Position(s) Centre-backTeam informationCurrent team Hà NộiNumber 16Youth career2007–2015 Hà NộiSenior career*Years Team Apps (Gls)2016– Hà Nội 139 (8)International career‡2017–2020 Vietnam U23 18 (3)2018– Vie...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Ben Johnson Medallista olímpico Datos personalesNombre completo Benjamin Sinclair JohnsonNacimiento Falmouth, Jamaica30 de diciembre de 1961 (62 años)Nacionalidad(es) Canadá CanadáAltura 1,77 m (5′ 10″)Peso 75 kg (165 lb)Carrera deportivaDeporte AtletismoSelección Canadá Canadá[editar datos en Wikidata] Benjamin Sinclair Ben Johnson (Falmouth, Jamaica, 30 de diciembre de 1961) es un exatleta canadiense conocido por su descalificación por dop...

Female ninja For other uses, see Kunoichi (disambiguation). Kunoichi (Japanese: くノ一, also くのいち or クノイチ) is a Japanese cant term for woman (女, onna).[1][2] In popular culture, it is often used for female shinobi or practitioner of ninjutsu (ninpo). The term was largely popularized by novelist Yamada Futaro in his novel Ninpō Hakkenden (忍法八犬伝) in 1964.[1] Although kunoichi have appeared in numerous creative works, including novels, TV-d...

Township in Minnesota, United StatesDewald Township, MinnesotaTownshipDewald Township, MinnesotaLocation within the state of MinnesotaShow map of MinnesotaDewald Township, MinnesotaDewald Township, Minnesota (the United States)Show map of the United StatesCoordinates: 43°37′33″N 95°45′51″W / 43.62583°N 95.76417°W / 43.62583; -95.76417CountryUnited StatesStateMinnesotaCountyNoblesArea • Total36.0 sq mi (93.3 km2) • Lan...

Commercial in London, England25 Cabot Square (The Cabot)General informationTypeCommercialArchitectural stylePost-modernLocationCanary WharfLondon, E14United KingdomCoordinates51°30′18″N 00°01′26.6″W / 51.50500°N 0.024056°W / 51.50500; -0.024056Current tenantsMorgan StanleyCompleted1991HeightRoof81 m (266 ft)Technical detailsFloor count17Floor area41,666.00 m2 (448,489.1 sq ft)Lifts/elevators12 (main)Design and constructionArchitect...

1 Tawarikh 18Kitab Tawarikh (Kitab 1 & 2 Tawarikh) lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab 1 TawarikhKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen13← pasal 17 pasal 19 → 1 Tawarikh 18 (atau I Tawarikh 18, disingkat 1Taw 18) adalah bagian dari Kitab 1 Tawarikh dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Dalam Alkitab Ibrani termasuk dalam bagian Ketuvim (כְּתוּבִים, tulisan).[1][2] Te...

Sporting event delegationSwitzerland at the1972 Winter OlympicsIOC codeSUINOCSwiss Olympic AssociationWebsitewww.swissolympic.ch (in German and French)in SapporoCompetitors52 (46 men, 6 women) in 6 sportsFlag bearerEdmund Bruggmann (alpine skiing)MedalsRanked 3rd Gold 4 Silver 3 Bronze 3 Total 10 Winter Olympics appearances (overview)192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022 Switzerland competed at the 1972 Winter Olympics in Sa...

Politics of Belize Constitution Human rights LGBT rights Monarchy Monarch Charles III Governor-General (list) Froyla Tzalam Government Prime Minister Johnny Briceño Cabinet Leader of the Opposition Moses Barrow National Assembly Senate President House of Representatives Speaker Administrative divisions Districts Constituencies Municipalities Local government Elections Recent elections General: 201220152020 Local: 201520182021 Political parties Foreign relations Ministry of Foreign Affairs M...

Zhangnama Zhang dalam aksara regularPengucapanIPA: /tʂɑŋ˥/ (Mandarin IPA)Zhāng (Pinyin)Tiuⁿ (Pe̍h-ōe-jī)BahasaTiongkok, Vietnam, KoreaAsalBahasaTiongkok LamaAsalNegara ZhangNama LainVarianChang, Zhang (Mandarin)Cheung (Kanton)Teo, Teoh (Hokkien, Teochew)Chong (Hakka)Trương, Trang (Vietnam)Jang, Chang (장) (Korea) Zhang adalah romanisasi pinyin dari nama Tionghoa paling umum yang ditulis 张 dalam karakter sederhana dan 張 dalam karakter tradisional. Kata ini diucapkan dalam nada...

この項目では、1997年生のAKB48の元メンバーについて記述しています。岡田奈々 (1959年生の元アイドル、女優)の同名の人物については「岡田奈々」をご覧ください。 おかだ なな岡田 奈々 国土交通省「C to Seaプロジェクト」アンバサダー任命式(2018年)生年月日 (1997-11-07) 1997年11月7日(26歳)出生地 日本・大阪府寝屋川市出身地 日本・神奈川県身長 157 cm血液型 A型職業 ...

Military unit size, usually composed of two or more squads or equivalent units This article is about a type of military unit. For other uses, see Platoon (disambiguation).Not to be confused with Pontoon or Splatoon.Platoon of marines from the United States Marine Corps, 1945 vteArmy units and organizationSubordinatedelement Fireteam / Crew Ø Squad ● Section / Patrol ●● Platoon / Troop / Flight ●●● Staffel / Echelon ●●●● ...