四邊形
| |||||||||||||||||||||||
Read other articles:

Shehu ShagariShagari pada tahun 1980 Presiden NigeriaMasa jabatan1 Oktober 1979 – 31 Desember 1983Wakil PresidenAlex Ekwueme PendahuluOlusegun Obasanjo sebagai Kepala Negara MiliterPenggantiMuhammadu Buhari sebagai Kepala Negara Militer Informasi pribadiLahir(1925-02-25)25 Februari 1925Shagari, Negara Bagian Sokoto, Protektorat NigeriaMeninggal28 Desember 2018(2018-12-28) (umur 93)Abuja, NigeriaPartai politikPartai Nasional NigeriaAnakMuhammad Bala Shagari Aminu Shehu ShagariK...

Asosiasi Sepak Bola Irlandia UtaraUEFADidirikan1880Kantor pusatBelfastBergabung dengan FIFA1911Bergabung dengan UEFA1954PresidenJim Shaw[1]Websitewww.irishfa.com Asosiasi Sepak Bola Irlandia Utara (Inggris: Irish Football Association (IFA)) adalah badan pengendali sepak bola di Irlandia Utara. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Irlandia Utara, yakni: Liga Asosiasi Sepak Bola Irlandia Utara Kejuaraan Asosiasi Sepak Bola Irlandia Utara Liga Intermediet Ballym...

Nieuwenkamp (Jan Toorop, 1923) Wijnand Otto Jan Nieuwenkamp alias W.O.J.N., (27 Juli 1874 – 23 April 1950) adalah seorang seniman berkebangsaan Belanda. Karier Nieuwenkamp (Pura Meduwe Karang) Setelah belajar sebentar di Amsterdamse Kunstnijverheidsschool, ia memantapkan diri sebagai seorang otodidak. Ia berkarya di Amsterdam, Timur Tengah, Jawa (1898), Bali (1904) dan Lombok (1906-1907), dan India Britania (1913-1914). Antara tahun 1917-1919 ia berkeliling Sumatra, Jawa, Bali...

American basketball player and coach George KingKing from The Monticola, 1962Personal informationBorn(1928-08-16)August 16, 1928Charleston, West Virginia, U.S.DiedOctober 5, 2006(2006-10-05) (aged 78)Naples, Florida, U.S.Listed height6 ft 0 in (1.83 m)Listed weight175 lb (79 kg)Career informationHigh schoolStonewall Jackson(Charleston, West Virginia)CollegeCharleston (1946–1950)NBA draft1950: 8th round, 89th overall pickSelected by the Chicago StagsPlaying care...

American track and field athlete Amy AcuffAcuff at the 2008 World Indoor ChampionshipsPersonal informationFull nameAmy Lyn AcuffNationalityAmericanBorn (1975-07-14) July 14, 1975 (age 48)Port Arthur, Texas, U.S.A.Height6 ft 2 in (1.88 m)Weight145 lb (66 kg)SportCountry United StatesSportTrack and fieldEventHigh jumpClubUCLA BruinsTeamUSA Track & Field Medal record Women's athletics Representing United States World University Games 1997 Sicily ...

Private university in Malaysia Wawasan Open UniversityUniversiti Terbuka Wawasan [1] (Malay)TypePrivateEstablished2006LocationGeorgetown, Penang, MalaysiaColours Light Green, and Dark GreenAffiliationsAsian Association of Open Universities (AAOU),[2] ICDE[3]Websitewww.wou.edu.my Wawasan Open University Main Campus in Penang, Malaysia Wawasan Open University Main Campus in Penang, Malaysia Wawasan Open University, abbreviated as WOU, is a private univer...

Genus of birds This article is about the bird. For other uses, see Avocet (disambiguation). Avocets Pied avocet (Recurvirostra avosetta) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Charadriiformes Family: Recurvirostridae Genus: RecurvirostraLinnaeus, 1758 Type species Recurvirostra avosetta (pied avocet)Linnaeus, 1758 Species Recurvirostra avosetta Recurvirostra americana Recurvirostra novaehollandiae Recurvirostra andina The four species...

Hong KongSpecial Administrative RegionSecretary for Housing 房屋局局長Emblem of Hong KongIncumbentWinnie Hosince 1 July 2022Housing BureauStyleThe HonourableAppointerCentral People's Governmentnomination by Chief ExecutiveInaugural holderIan Macdonald LightbodyFormation1973; 51 years ago (1973)WebsiteHB Secretary for HousingTraditional Chinese房屋局局長Simplified Chinese房屋局局长TranscriptionsStandard MandarinHanyu PinyinFángwū Jú JúzhǎngYue: C...

This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (August 2014) (Learn how and when to remove this message) Official Logo Jumeirah Garden City master plan overlook The master plan of Jumeirah Garden City refers to the re-development of a 9,000,000-square-metre (97,000,000 sq ft) land area, conceptualized to be a part of the 2015 strategic pla...

First marshal of Phoenix, Arizona (1851–1896) Henry GarfiasSheriff GarfiasBornEnrique Garfias1851Orange County, California, U.S.DiedMay 8, 1896Phoenix, ArizonaOccupation(s)Lawman, rancher, assessor, tax collector, constable, pound master, and street superintendentKnown forHighest elected Mexican American official in Arizona during the 19th centuryOpponentVariousSpouseElena RedondoChildrenLouis GrafiasParent(s)Manuel Garfias and Maria Luisa Avila Henry Garfias (born Enrique Garfias; 185...

Para otros usos de este término, véase Greiff.León de Greiff Información personalNombre de nacimiento Francisco de Asís León Bogislao de Greiff HäuslerNacimiento 22 de julio de 1895Medellín, Antioquia, ColombiaFallecimiento 11 de julio de 1976 (80 años)Bogotá, ColombiaSepultura Cementerio Central de Bogotá Nacionalidad ColombianoLengua materna EspañolFamiliaCónyuge María Teresa Matilde Bernal Nicholls (1927 - † 1966)Hijos Astrid de Greiff BernalBoris de Greiff BernalHjal...

Political group in the European Parliament Europe of Freedomand Direct DemocracyEuropean Parliament groupEurope of Freedom and Direct Democracy Group logoNameEurope of Freedom and Direct DemocracyEnglish abbr.EFDDFrench abbr.ELDDFormal nameEurope of Freedom and Direct Democracy Group in the European ParliamentIdeologyEuroscepticism[1][2][3]Right-wing populism[4]Direct democracy[5]Political positionRight-wing[6] to far-right[7][8...

Annual association football award Not to be confused with Best Footballer in Asia. The Asian Footballer of the Year award is an annual prize awarded to the best Asian player in a calendar year. History A football handbook took a poll about who was the best Asian footballer in 1985, and this poll is regarded as the origin of the Asian footballer award.[1][2] However, it was not a selection of clear process or official organization, and is generally excluded from the list.[3...
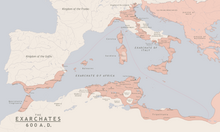
Territory ruled by an exarch This article may be in need of reorganization to comply with Wikipedia's layout guidelines. Please help by editing the article to make improvements to the overall structure. (January 2016) (Learn how and when to remove this message) An exarchate is any territorial jurisdiction, either secular or ecclesiastical, whose ruler is called an exarch. Byzantine Emperor Maurice created the first exarchates in the recently reconquered provinces of the former Western Empire....

Property of economic goods Wild fish stocks are a rivalrous good, as the amount of fish caught by one boat reduces the number of fish available to be caught by others. In economics, a good is said to be rivalrous or a rival if its consumption by one consumer prevents simultaneous consumption by other consumers,[1] or if consumption by one party reduces the ability of another party to consume it. A good is considered non-rivalrous or non-rival if, for any level of production, the cost ...

Menunggu GodotSampul edisi Indonesia, 1978PenulisSamuel BeckettTokohVladimirEstragonPozzoLucky BocahMuteGodotPementasan perdana5 Januari 1953; 71 tahun lalu (1953-01-05)Pentas perdanaThéâtre de Babylone [fr], ParisBahasa asliPrancisGenreTragicomedy (drama) Menunggu Godot (/ˈɡɒdoʊ/ GOD-oh)[1] adalah sebuah lakon drama karya Samuel Beckett. Menceritakan tentang dua karakter, Vladimir (Didi) dan Estragon (Gogo), terlibat dalam berbagai diskusi dan pertemuan sambil...

1956 studio album by Frank FosterNo 'CountStudio album by Frank FosterReleased1956RecordedMarch 5 and 7, 1956StudioVan Gelder Studio, Hackensack, New JerseyGenreJazzLength35:08LabelSavoyMG 12078ProducerOzzie CadenaFrank Foster chronology Hope Meets Foster(1955) No 'Count(1956) Basie Is Our Boss(1962) No 'Count is an album by saxophonist Frank Foster recorded in 1956 and released on the Savoy label.[1] Reception Professional ratingsReview scoresSourceRatingAllmusic[2] A...

Town in Victoria, AustraliaOcean GroveVictoriaOne of the many beaches at Ocean GroveOcean GroveCoordinates38°15′0″S 144°31′0″E / 38.25000°S 144.51667°E / -38.25000; 144.51667Population14,165 (2016 census)[1]Postcode(s)3226Location 98 km (61 mi) SW of Melbourne 23 km (14 mi) SE of Geelong LGA(s)City of Greater GeelongState electorate(s)BellarineFederal division(s)Corangamite Localities around Ocean Grove: Wallington Wallingt...

1640s minor war in India Willem Leyel's war on GolcondaElephant hunt in Danish Tranquebar, presumably early 19th century.Datec. 1645LocationCoromandel CoastResult InconclusiveTerritorialchanges Status quo ante bellumBelligerents Danish India Golconda SultanateCommanders and leaders Willem Leyel Abdullah QutbUnits involved Christianshavn UnknownStrength Ukn. amount of ships Ukn. amount of shipsCasualties and losses Negligible Some shipsvteDanish colonial conflictsBaltic Sea Wendish...

German historian and diplomat This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ludwig von Pastor – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how and when to remove this message) Ludwig von PastorBorn31 January 1854Aachen, Kingdom of PrussiaDied30 September 1928Innsbruck, Austria Ludwig...