椭圆曲线
|
Read other articles:

DEL48Informasi latar belakangAsalDelhi, IndiaGenrePop, V-pop, J-pop, Teen Pop, Bubblegum PopTahun aktif2019 (2019)–2020 (2020)Artis terkaitAKB48 GroupSitus webdel48.comAnggotaAnggota DEL48Mantan anggotaLihat selengkapnya... DEL48 (dibaca D.E.L. Forty-Eight) adalah sebuah grup vokal perempuan idola India dan grup saudari internasional ketujuh AKB48. Grup tersebut diambil dari nama Delhi, India. Bersama dengan MUB48, DEL48 diumumkan pada 19 Juni 2019.[1] Pada tanggal 16 Okto...

Brian LittrellLittrell in June 2011LahirBrian Thomas Littrell20 Februari 1975 (umur 49)Lexington, Kentucky, ASNama lainBrian T. LittrellB-RokBriSeaverBFrickAlmamaterTates Creek High SchoolPekerjaanPenyanyipenulis laguaktorTahun aktif1993–sekarangSuami/istriLeighanne Wallace (m. 2000)AnakBaylee Littrell (l. 2002)KerabatKevin Richardson (sepupu)Karier musikGenrePopR&BCCMInstrumenVokalgitarLabelReunionJiveArtis terkaitBackstreet BoysNKOTBSBSit...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Semi-permanent joint between two ropes This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rope splicing – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Stages in splicing the end of a rope, from Scientific American, 1871 Rope splicing in ropewor...

Kaisar Jerman Bekas Kerajaan Imperial Lambang kekaisaran Wilhelm II Penguasa pertama Wilhelm I Penguasa terakhir Wilhelm II Gelar His Imperial and Royal Majesty Kediaman resmi Stadtschloss, Berlin Penunjuk Turun-temurun Pendirian 18 Januari 1871 Pembubaran 28 November 1918 Penuntut takhta Georg Friedrich Wilhelm I. Friedrich III. Wilhelm II Kaisar Jerman (Jerman: Deutscher Kaisercode: de is deprecated ) adalah gelar resmi dari kepala negara Kekaisaran Jerman (Jerman: Deutsches Kaiserreichcod...
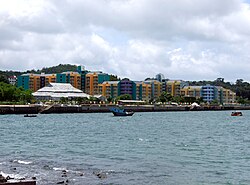
Public housing estate in Peng Chau, Hong Kong Kam Peng EstateKam Peng Estate and Peng Lai CourtGeneral informationLocation21 Peng Lei Road, Peng ChauNew Territories, Hong KongCoordinates22°17′14″N 114°02′14″E / 22.287100°N 114.037200°E / 22.287100; 114.037200StatusCompletedCategoryPublic rental housingNo. of blocks1[1]No. of units261[1]ConstructionConstructed1996; 28 years ago (1996)AuthorityHong Kong Housing Authority Kam ...
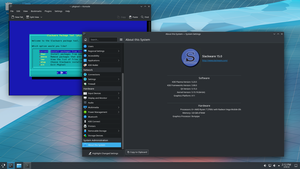
Linux distribution (operating system) This article is about the Linux distribution. It is not to be confused with Slack (software). SlackwareSlackware 15.0 with KDE Plasma 5 as the desktop environmentDeveloperPatrick VolkerdingOS familyLinux (Unix-like) (based on Softlanding Linux System)Working stateCurrentSource modelOpen sourceInitial release17 July 1993; 30 years ago (1993-07-17)[1]Latest release15.0[2] [3][4] / 2 February 2022;&#...

Soyuz TMA-20MSoyuz TMA-20M mendekati ISSOperatorRoscosmosCOSPAR ID2016-018ASATCAT no.41391Durasi misi172 hari 3 jam 47 menit Properti wahanaJenis wahana antariksaSoyuz-TMA-M 11F747 No.720[1]ProdusenRKK Energia AwakJumlah awak3AwakAleksey OvchininOleg SkripochkaJeffrey N. WilliamsTanda panggilBurlak Awal misiTanggal luncur18 Maret 2016 21:26:38 UTCRoket peluncurSoyuz-FGTempat peluncuranBaikonur 1/5 Akhir MisiTanggal mendarat7 September 201601:13 UTCTempat pendaratanKazakhstan Parameter...

ملكة جمال العالم 2007 زهانغ زيلين ، حاملة لقب مسابقة ملكة جمال العالم 2007 تاريخ العرض 01 ديسمبر 2007 مقدم الحفل أنجيلا تشاوفرناندو أليند ضيف شرف دنكان جايمسهايكوجوقة مفيزو جنوب إفريقيارقم 9 مدرسة سانيا الابتدائية مكان مسرح تاج الجمال، سانيا، الصين البث التلفيزيوني إي!أس أم جي م...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

This is a list of hills in Cornwall based on data compiled in various sources, but particularly the Database of British and Irish Hills, Jackson's More Relative Hills of Britain[1] and the Ordnance Survey 1:25,000 Explorer and 1:50,000 Landranger map series. Many of these hills are important historic, archaeological and nature conservation sites, as well as popular hiking and tourist destinations in the county of Cornwall in southwest England. Colour key Class Prominence Marilyns 150...

Society controlled by business corporations This article is about the idea of government dominated by corporate business interests. For the functions and interests of the state in a capitalist society, see Capitalist state. For capitalist economies dominated by corporations, see Corporate capitalism. Not to be confused with corporatism, which is the organization of a society into groups which are determined by their collective common interests. This article has multiple issues. Please help im...

.كنيسة مارمرقس القبطية، تعد الكنيسة القبطية الأرثوذكسية إحدى أكبر التجمعّات المسيحية في العالم الإسلامي. تترواح أعداد المسيحيين في العالم الإسلامي بين 139-144 مليون حسب جدول مركز بيو للأبحاث؛ وبين 153 مليون إلى 230 مليون حسب إحصائيات أخرى.[1][2][3] بعيد القرن السابع بن...

Cuisine originating from the Sichuan province of China Sichuan cuisineKung Pao chickenChinese四川菜TranscriptionsStandard MandarinHanyu PinyinSìchuān càiChuan cuisineChinese川菜TranscriptionsStandard MandarinHanyu PinyinChuān cài Part of a series onChinese cuisine Regional cuisines Four Great Traditions Chuan (Sichuan) Lu (Shandong) Yue (Guangdong) Huaiyang (Jiangsu) Eight Great Traditions(+all above) Anhui Fujian Hunan Zhejiang Ten Great Traditions(+all above) Beijing Shanghai Twel...

2019 Washington Justice seasonHead coachKim Hyeong-seokGeneral managerAnalynn DangOwnerMark EinDivisionAtlanticResultsRecord8–20 (.286)PlaceAtlantic: 8thLeague: 17thStage 1 PlayoffsDid not qualifyStage 2 PlayoffsDid not qualifyStage 3 PlayoffsDid not qualifySeason PlayoffsDid not qualify Washington Justice 2020 → The 2019 Washington Justice season was the first season of Washington Justice's existence in the Overwatch League as one of eight expansion franchises added for the...

Sporza est le label des émissions sportives du groupe Vlaamse Radio- en Televisieomroep en radio, télévision, web et multimédia. En télévision, Sporza émet ses programmes sur één, Canvas et le troisième canal de la VRT. À l'origine, Sporza était une chaîne de télévision à part entière. Créée le 31 mai 2004 à l’occasion des Jeux olympiques d’Athènes, Sporza occupa un canal propre pendant 96 jours (du 31 mai au 3 septembre 2004) avant de perdre ce canal. Depuis, elle d...

American railroad company For other uses, see Panhandle Railroad. Panhandle and Santa Fe RailwayAbandoned P&SF depot in Littlefield, TexasOverviewHeadquartersAmarillo, TexasLocaleNew Mexico, Oklahoma, TexasDates of operation1886–1965PredecessorSouthern Kansas Railway Company of TexasSuccessorAtchison, Topeka and Santa Fe RailwayTechnicalTrack gauge4 ft 8+1⁄2 in (1,435 mm) standard gaugeOtherWebsiteHandbook of Texas The Panhandle and Santa Fe Railway (P&...

Piptobak Den här artikeln behöver källhänvisningar för att kunna verifieras. (2017-05) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. Piptobak är tobak iordninggjord för att användas i rökpipa. Piptobaken är oftast strimlad i olika finhetsgrad. Piptobak förvarades traditionellt i en tobakspung eller tobaksburk för att den skulle hålla f...

Outdated diagnosis for patients with multiple symptoms of a neurological condition This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (September 2023) (Learn how and when to remove this message) Medical conditionFemale hysteriaWomen with hysteria under the effects of hypnosis, 1876–1880Spec...

Giovanni Spano Giovanni Spano (Ploaghe, 3 marzo 1803 – Cagliari, 3 aprile 1878) è stato un archeologo, linguista, etnologo, docente universitario e presbitero italiano. Indice 1 Biografia 2 Opere 3 Onorificenze 4 Note 5 Bibliografia 6 Voci correlate 7 Altri progetti 8 Collegamenti esterni Biografia Nato da famiglia agiata, lascia Ploaghe nel 1812 alla volta di Sassari dove viene iscritto alla scuola degli Scolopi. Nel 1820 riceve il titolo di Magister artium liberalium dopo aver frequentat...

































