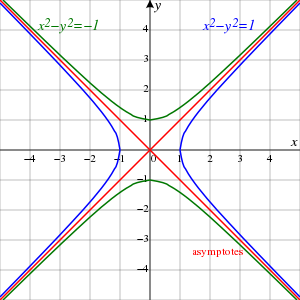
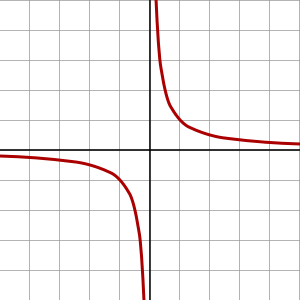
双曲线
|
Read other articles:

Untuk zat dalam kimia, lihat Katalis. The CatalystSingel oleh Linkin Parkdari album A Thousand Suns dan Medal of HonorSisi-BNew Divide (Live)Dirilis02 Agustus 2010 (2010-08-02)FormatCD, unduhan digitalDirekam2008–2010GenreElectronic rock,[1] techno[2]Durasi5:42LabelWarner Bros.PenciptaLinkin ParkProduserRick Rubin, Mike ShinodaKronologi singel New Divide (2009) The Catalyst (2010) Waiting for the End ((2010)) Video musikThe Catalyst di YouTube The Catalyst adalah lagu k...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of accolades received by The Theory of Everything di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika An...

I distretti pomereliani di Lauenburg e Bütow, identificati da Lb. e Bt., assoggettati ai duchi della Pomerania (nel 1526) La Terra di Lauenburg e Bütow[1][2][3] (in tedesco Länder o Lande Lauenburg und Bütow, in polacco Ziemia lęborsko-bytowska) costituì una regione storica della Pomerania orientale. Composta da due distretti incentrati intorno alle città di Lauenburg (oggi Lębork) e Bütow (Bytów), costituiva la periferia occidentale della Pomerelia...

Way to determine the position of a fetus inside the woman's uterus Leopold's maneuvers In obstetrics, Leopold maneuvers are a common and systematic way to determine the position of a fetus inside the woman's uterus. They are named after the gynecologist Christian Gerhard Leopold. They are also used to estimate term fetal weight.[1] The maneuvers consist of four distinct actions, each helping to determine the position of the fetus. The maneuvers are important because they help determin...
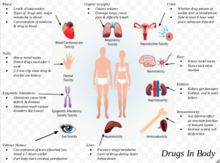
Use of toxicology for investigations Forensic toxicology is a multidisciplinary field that combines the principles of toxicology with expertise in disciplines such as analytical chemistry, pharmacology and clinical chemistry to aid medical or legal investigation of death, poisoning, and drug use.[1] The paramount focus for forensic toxicology is not the legal implications of the toxicological investigation or the methodologies employed, but rather the acquisition and accurate interpre...

Event from the Gospel of Luke Supper at Emmaus redirects here. For other uses, see Supper at Emmaus (disambiguation). Jesus and the two disciples On the Road to Emmaus, by Duccio, 1308–1311, Museo dell'Opera del Duomo, Siena According to the Gospel of Luke, the road to Emmaus appearance is one of the early post-resurrection appearances of Jesus after his crucifixion and the discovery of the empty tomb.[1][2][3] Both the meeting on the road to Emmaus and the subsequen...

Undergarment worn in Ancient Rome SubligaculumFemale athletes wearing a bikini-like combination of a subligaculum and a strophium (breast-cloth)(Sicily, c. 300 AD)TypeUndergarment Bikini-like leather subligaculum found in excavations of Roman London (Museum of London) A subligaculum was a kind of underwear worn by ancient Romans. It could come either in the form of a pair of shorts, or in the form of a simple loincloth wrapped around the lower body. It could be worn both by men and women...

جبل سلع الموقع السعودية إحداثيات 24°28′30″N 39°35′58″E / 24.475°N 39.59944444°E / 24.475; 39.59944444 الارتفاع 2148 قدم تعديل مصدري - تعديل 24°28′30″N 39°35′58″E / 24.47500°N 39.59944°E / 24.47500; 39.59944 (جبل سلع) جبل سلع ومسجد الفتح بمنطقة السبع مساجد جبل سلع أحد جبال ال�...

Voce principale: Società Sportiva Calcio Napoli. AC NapoliStagione 1946-1947 Sport calcio Squadra Napoli Allenatore Raffaele Sansone Presidente Pasquale Russo Direttore sportivo Attila Sallustro[1] Serie A8º Maggiori presenzeCampionato: Busani, Rosi (38)Totale: Busani, Rosi (38) Miglior marcatoreCampionato: Busani (12)Totale: Busani (12) Stadiodella Liberazione 1945-1946 1947-1948 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'As...

Vilayet di BasraVilayet di Basra - LocalizzazioneIl vilayet di Basra nell'anno 1900 Dati amministrativiNome completoVilâyet-i Basra Nome ufficialeولايت بصره Lingue ufficialiturco ottomano Lingue parlateturco ottomano, arabo CapitaleBasra Dipendente daImpero ottomano PoliticaForma di StatoVilayet Forma di governoVilayet elettivo dell'Impero ottomano Capo di StatoSultani ottomani Nascita1875 Fine1918 CausaArmistizio di Mudros Territorio e popolazioneBacino geograficoIraq Massima esten...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

George Mikan PosisiPemain Tengah JulukanMr. BasketballTinggi6 ft 10 in (2,08 m) Berat245 lb (111 kg)Negara Amerika SerikatLahir(1924-06-18)18 Juni 1924 Joliet, IllinoisWafat1 Juni 2005(2005-06-01) (umur 80)Scottsdale, ArizonaKuliahDePaulKarier pro1946 – 1956Klub sebelumnya Chicago American Gears George Lawrence Mikan, Jr. (18 Juni 1924 – 1 Juni 2005) adalah seorang pemain bola basket amatir liga NBA, BBA, dan NBL di Amerika Serikat. Ge...

Questa voce sull'argomento dipartimenti della Francia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. MarnadipartimentoMarne LocalizzazioneStato Francia RegioneGrande Est AmministrazioneCapoluogoChâlons-en-Champagne (sottoprefetture: Épernay, Reims, Sainte-Menehould, Vitry-le-François) Presidente del Consiglio dipartimentaleRené-Paul Savary (UMP) TerritorioCoordinatedel capoluogo48°57′27″N 4°21′54″E48°57′27″N, 4°21′54″...

Railway line in Japan Joban LineJJ JLJoban Line Series E531OverviewNative name常磐線Owner JR EastLocaleTokyo, Chiba, Ibaraki, Fukushima, Miyagi prefecturesTerminiNippori (services extended to Shinagawa)Iwanuma (services extended to Sendai (Miyagi))Stations85 on the Joban Line4 on the Ueno-Tokyo LineServiceTypeHeavy railOperator(s)JR East, JR FreightHistoryOpened16 January 1889; 135 years ago (1889-01-16)Completed1 April 1905; 119 years ago (1905-04-01)Te...

Municipality in the Mexican state of Chihuahua Municipality in Chihuahua, MexicoPráxedis G. GuerreroMunicipalityMunicipality of Práxedis G. Guerrero in ChihuahuaPráxedis G. GuerreroLocation in MexicoCoordinates: 31°22′N 106°18′W / 31.367°N 106.300°W / 31.367; -106.300Country MexicoStateChihuahuaMunicipal seatPráxedis Gilberto GuerreroMunicipality created15 February 1859Municipality dissolved1893Municipality restoredFebruary 1922Area • Total...

الاتحاد الدولي لكرة اليد الاسم المختصر IHF الرياضة كرة يد أسس عام 11 يوليو، 1946 الرئيس حسن مصطفى المقر بازل الانتسابات 159 اتحاد وطني الموقع الرسمي http://www.ihf.info تعديل مصدري - تعديل الاتحاد الدولي لكرة اليد (بالإنجليزية: International Handball Federation، يختصر IHF) هو الهيئة المنظمة لريا�...

Ciudad metropolitana de VeneciaCittà metropolitana di Venezia Ciudad metropolitana BanderaEscudo Coordenadas 45°26′23″N 12°19′55″E / 45.4397, 12.3319Capital VeneciaEntidad Ciudad metropolitana • País Italia • Región VénetoAlcalde metropolitano Luigi Brugnaro (independiente de centroderecha)Municipios 44Superficie • Total 2462 km²Población • Total 858 544 hab. • Densidad 348,5 hab./km²Huso horario...

Cet article est une ébauche concernant Caen. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Le soulèvement de Caen contre la Convention nationale est une insurrection fédéraliste qui eut lieu à Caen et en Normandie de juin à juillet 1793. Origine La crise remonte au printemps 1793 où Girondins et Montagnards se déchirent à la Convention...

Staumauer des Kraftwerks Ottenstein mit dem Krafthaus, in welchem zwei Pumpen mit je 9 MW Leistung und vier Turbinen mit je 12 MW Leistung untergebracht sind Das Koepchenwerk in Herdecke Pumpspeicherwerk Markersbach – Oberbecken Ein Pumpspeicherkraftwerk, auch Pumpspeicherwerk, abgekürzt PSW, ist ein Speicherkraftwerk, das elektrische Energie in Form von potentieller Energie (Lageenergie) in einem Stausee speichert. Das Wasser wird durch elektrische Pumpen in den Speicher gehoben...

Een gametofyt is, binnen de levenscyclus van planten en algen met geslachtelijke voortplanting, de generatie ('het stadium') die de nieuwe gameten vormt. Als de gametofyt diploïde is, worden de gameten in gametangia gevormd door (gametische) meiose (reductiedeling), maar als de gametofyt haploïde is, worden de gameten door gewone celdeling, mitotisch gevormd. Dit laatste komt het meeste voor. Levenscyclus Spermatozoïden. Veel organismen en met name planten (in wijdere zin) zijn diplohaplon...