摆线
|
Read other articles:

MakapiliMakabayang Katipunan ng mga PilipinoPendirianNovember 1944Pembubaran1945Negara Republik Filipina KeduaMotifDukungan untuk pendudukan Filipina oleh JeoangJumlah anggota4.000–6.000← Didahului olehPartai Ganap Makabayang Katipunan ng mga Pilipino (Asosiasi Patriotik Filipina), yang lebi dikenal sebagai Makapili, adalah sebuah kelompok militan yang dibentuk di Filipina pada 1944 pada Perang Dunia II untuk memberikan bantuan militer kepada Angkatan Darat Kekaisaran J...

Bangkok DangerousThe teaser release posterSutradaraDanny Pang PhatOxide Pang ChunProduserNorman GolightlyGraham KingWilliam SherakJason ShumanDitulis olehDanny Pang PhatOxide Pang ChunJason RichmanPemeranNicolas CageCharlie YeungChakrit YamnamNaratorNicolas CagePenata musikBrian TylerSinematograferDecha SrimantraPenyuntingMichael JacksonCurran PangDistributorInitial Entertainment Group(all countries except North America)Lionsgate (North America)Tanggal rilis 5 September 2008 (2008-...

2012 South Korean filmThe WeightHangul무게Revised RomanizationMugeMcCune–ReischauerMuge Directed byJeon Kyu-hwanWritten byJeon Kyu-hwanProduced byKim Woo-taek Choi Min-aeStarringCho Jae-hyun Park Ji-aCinematographyKim Nam-gyunEdited byKim Mi-yeong Park Hae-ohMusic byJu Dae-gwanDistributed byNext Entertainment WorldRelease dates September 7, 2012 (2012-09-07) (Venice International Film Festival) November 7, 2013 (2013-11-07) (South Korea) Running time1...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WPHI-FM – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this template message) Radio station in Pennsylvania, United StatesWPHI-FMSimulcast of KYW, PhiladelphiaJenkintown, PennsylvaniaUnited StatesBroadcast areaGreater Ph...

Pour les articles homonymes, voir Hoeffel. Daniel Hoeffel Daniel Hoeffel en 2013. Fonctions Sénateur français 2 octobre 1995 – 30 septembre 2004(8 ans, 11 mois et 28 jours) Élection 24 septembre 1995 Circonscription Bas-Rhin Groupe politique UC puis UMP Prédécesseur Philippe Richert Successeur Joseph Ostermann 28 septembre 1981 – 29 avril 1993(11 ans, 7 mois et 1 jour) Élection 27 septembre 1981 (partielle) Réélection 28 septembre 1986 Circonscriptio...

2011 video gameThe Sims SocialDeveloper(s)PlayfishPublisher(s)Electronic ArtsWriter(s)Sean BaityPlatform(s)Facebook PlatformReleaseAugust 9, 2011Genre(s)Dating sim, Social simulation The Sims Social was a Facebook addition to the Sims series of video games. It was announced during the Electronic Entertainment Expo 2011 press conference. As with the original Sims games, The Sims Social lets the user create their own customizable character. In this version, however, the player uses their charac...

Time zone data for this US state Time in Massachusetts, as in all US states, is regulated by the United States Department of Transportation.[1] Massachusetts is in the Eastern Time Zone (ET) and observes daylight saving time (DST). Time in Massachusetts Time UTC Standard time (winter) Eastern Standard Time (EST) UTC−05:00 Daylight time (summer) Eastern Daylight Time (EDT) UTC−04:00 Independent of daylight saving time, solar noon on the March equinox is about 12:00 in Wester...

Bronze Age culture of the Indo-Gangetic Plain Ochre Coloured Pottery cultureOchre Coloured Pottery finds ( c.2600 - 1200 BCE )Geographical rangeNorth IndiaPeriodBronze AgeDatesc. 2000–1500 BCEMajor sitesAhichchhatraBahadrabadBargaonBisauliFatehgarhHastinapurHulasJhinjhanaKatpalon KausambiMitathalRed fortSinauliMapCharacteristicsExtensive copper metallurgyBurials with pots and copper weaponsPreceded byNeolithicFollowed byBlack and red warePainted Grey Ware culture History of South Asia Outli...

American businessman and politician Craig Greenberg51st Mayor of LouisvilleIncumbentAssumed office January 2, 2023Preceded byGreg Fischer Personal detailsBorn (1973-08-22) August 22, 1973 (age 50)Commack, New York, U.S.Political partyDemocraticSpouseRachelChildren2EducationUniversity of Michigan (BS)Harvard University (JD)WebsiteCampaign website Craig Greenberg (born August 22, 1973) is an American businessman, lawyer, and politician[1] serving as the third mayor of Louisvill...

Southern California transit company Red Car redirects here. For the taxis of Hong Kong, see Taxicabs of Hong Kong. For the British town, see Redcar. Pacific ElectricPacific Electric Building and Main StreetOverviewHeadquartersLos Angeles, CaliforniaReporting markPELocaleGreater Los Angeles AreaDates of operation1901–1961 (passenger), 1965 (freight)SuccessorSouthern Pacific (freight)Los Angeles Metropolitan Transit Authority, Los Angeles Metro Rail (passenger)TechnicalTrack gauge4 f...
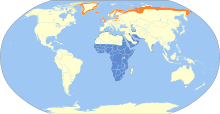
Species of bird Common ringed plover AdultCalls recorded in Norfolk, England Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Charadriiformes Family: Charadriidae Genus: Charadrius Species: C. hiaticula Binomial name Charadrius hiaticulaLinnaeus, 1758 The common ringed plover or ringed plover (Charadrius hiaticula) is a small plover that breeds across much of northern Eurasia, a...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

قلب الليل معلومات الكتاب المؤلف نجيب محفوظ الناشر مكتبة مصر تاريخ النشر 1975م تعديل مصدري - تعديل قلب الليل، هي رواية صغيرة الحجم نسبيا للروائي نجيب محفوظ، والصادرة في 155 صفحة عن مكتبة مصر، وصدرت طبعتها الأولى عام 1975م وقامت دار الشروق بإعادة طباعتها في العام 2006م.[1] تح...

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (December 2022) (Learn how and when to remove this message) Overview of the events of 2009 in Australian television List of years in Australian television … 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 … Art Archaeology Architecture Literature...

Untuk orang lain dengan nama yang sama, lihat George Carey. Yang Mulia dan Right HonourableThe Lord Carey of CliftonPCmantan Uskup Agung CanterburyGerejaGereja InggrisProvinsi gerejawiProvinsi CanterburyKeuskupanKeuskupan Canterburydidelegasikan menjadi Uskup DoverMasa jabatan1991–2002PendahuluRobert RunciePenerusRowan WilliamsJabatan lainUskup asisten kehormatan di Swansea & Brecon (2004–?), dalam Southwark dan di Bristol; di Oxford (?–2017)Life peer (2002);Uskup Bath dan Well...

Questa voce sugli argomenti biochimici e chimici tedeschi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Feodor Felix Konrad Lynen Premio Nobel per la medicina 1964 Feodor Felix Konrad Lynen (Monaco di Baviera, 6 aprile 1911 – Monaco di Baviera, 6 agosto 1979) è stato un biochimico tedesco, premio Nobel per la medicina nel 1964, insieme a Konrad Bloch, per le scoperte sul metabolismo degli acidi grassi e del colesterolo[1]. Indice 1 Bi...

Fatahillah Square, the restored 18th-century water pump, and the Jakarta History Museum. Fatahillah Square (Indonesian: Taman Fatahillah) is the historical center of the old Batavia. The square is located at the center of Jakarta Old Town. Today the square is a tourist area home to the Jakarta History Museum, Wayang Museum and Fine Art and Ceramics Museum in Kota, Jakarta. History Pre-1632 layout From the beginning of its foundation, Batavia was a well-planned Dutch forted city.[1] Th...

Like a VirginAlbum studio karya MadonnaDirilis12 November 19845 Agustus 1985 (Re-release)21 May 2001 (Remastered)DirekamApril - September 1984 di Power Station Studios, Manhattan, New York[1]GenreDance-Pop[2]Durasi43:10LabelSire Records, Warner Bros. Warner Bros. (2001)ProduserMadonna, Nile Rodgers, Stephen BrayKronologi Madonna Madonna(1983)Madonna1983 Like a Virgin(1984) True Blue(1986)True Blue1986 Like a Virgin adalah album kedua penyanyi pop Amerika Serikat Madonna, y...

Military airbase in Russia You can help expand this article with text translated from the corresponding article in Russian. (July 2011) Click [show] for important translation instructions. View a machine-translated version of the Russian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated te...

Cet article est une ébauche concernant une localité de Castille-et-León. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. El Bohodón Héraldique Drapeau Église Notre-Dame de l'Assomption à El Bohodón Administration Pays Espagne Communauté autonome Castille-et-León Province Province d'Ávila Code postal 05165 Démographie Population 107 hab. (2023) Densité 4,9 hab./km2 Géographie Coordonnées ...













