超方形
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:
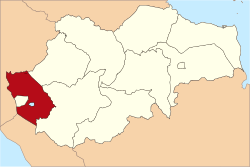
Peta Lokasi Kabupaten Kerinci di Jambi Berikut ini adalah daftar kecamatan dan kelurahan/desa di kabupaten Kerinci, Provinsi Jambi, Indonesia. Kabupaten Kerinci memiliki 18 kecamatan, 2 kelurahan dan 285 desa (dari total 141 kecamatan, 163 kelurahan dan 1.399 desa di seluruh Jambi). Pada tahun 2017, jumlah penduduknya sebesar 235.735 jiwa dengan luas wilayahnya 3.355,27 km² dan sebaran penduduk 70 jiwa/km².[1][2] Berdasarkan data Direktorat Jenderal Kependudukan dan Pencatat...

Disambiguazione – Se stai cercando la Serie D in altri sport, vedi Serie D (disambigua). Serie DSport Calcio TipoClub FederazioneFIGC Paese Italia OrganizzatoreLega Nazionale Dilettanti TitoloCampione d'Italia di Serie D Cadenzaannuale Aperturasettembre Chiusuramaggio Partecipanti166 squadre[1] Formula9 gironi all'italiana + play-off e play-out Promozione inSerie C Retrocessione inEccellenza Sito Internetseried.lnd.it StoriaFondazione1948-1949 Numero edizioni75 Detentore ...

Representations of pirates in fiction or literature This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pirates in the arts and popular culture – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this template message) Engraving of the English pirate Blackbeard from the 1724 ...

River in Bacău, RomaniaUzLocationCountryRomaniaCountiesHarghita, BacăuVillagesEghersec, Valea Uzului, DărmăneștiPhysical characteristicsSourceCiuc Mountains MouthTrotuș • locationDărmănești • coordinates46°21′52″N 26°30′55″E / 46.3645°N 26.5152°E / 46.3645; 26.5152Length50 km (31 mi)Basin size469 km2 (181 sq mi)Basin featuresProgressionTrotuș→ Siret→ Danube→ Black Sea The Uz ...

Pipa vulkanik. Pipa vulkanik adalah struktur geologis bawah tanah yang dibentuk oleh letusan supersonik gunung berapi. Pipa vulkanik dipandang sebagai jenis dari diatrema. Pipa vulkanik tersusun atas magma beku yang membentuk kerucut kurus yang dalam (disebut sebagai berbentuk wortel), dan biasanya terdiri dari satu atau dua jenis batuan karakteristik, yakni kimberlit atau lamproit. Batuan ini mencerminkan komposisi sumber magma di bawah gunung berapi, di mana Bumi kaya akan magnesium. Pipa v...

Cet article est une ébauche concernant une unité ou formation militaire américaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Emblème de l'unité. La 1re escadre d'opérations spéciales est la plus grosse unité de l'US Air Force assignée à l'United States Special Operations Command. Sa base opérationnelle se trouve à Hurlburt Field et environ 8 000 militaires et 700 civils servent en so...

This film-related list is incomplete; you can help by adding missing items. (August 2008) Cinema of Greece List of Greek films Pre 1940 1940s 1950s 1960s 1970s 1980s 1990s 2000s 2010s 2020svte A list of notable films produced in Greece in the 1990s. 1990s Title Director Cast Genre Notes 1990 Singapore Sling(Singapore Sling: Ο Άνθρωπος που Αγάπησε ένα Πτώμα) Nikos Nikolaidis Meredyth Herold, Panos Thanassoulis, Michele Valley Drama 3 Awards in Thessaloniki Film Fest...

Antonov An-14 Pchelka (bahasa Rusia: «Пчелка», Little Bee, (nama pelaporan NATO: Clod) adalah pesawat utilitas Soviet yang pertama kali diterbangkan pada 15 Maret 1958. Itu adalah transportasi STOL utilitas ringan bermesin twin. Penerus An-14, An-28 dengan mesin turboprop, masih diproduksi di pabrik-pabrik PZL Mielec di Polandia di bawah nama-nama PZL M28 Skytruck dan PZL M28B Bryza. Dengan karakteristik penerbangan yang sangat stabil, An-14 bisa diterbangkan oleh sebagian besar sete...

علم الفلكحقل هابل العميق الأقصى صدر في 25 سبتمبر 2012، هو صورة لجزء من الفضاء في مركز صورة حقل هابل العميق الفائق. يحتوي على ما يقدر بـ5500 مجرة، أقدمها يُنظر إليها كما كانت منذ 13.2 مليار سنة مضت.[1][2]صنف فرعي من علوم طبيعيةيمتهنه عالم فلكفروع علم الفلك الرصدي، علم الفلك ال...

Academic and policy-relevant field on problems in the nuclear weapons and energy complex Nuclear weapons Background Nuclear explosion History Warfare Design Testing Delivery Yield Effects Winter Workers Ethics Arsenals Arms race Espionage Proliferation Disarmament Terrorism Opposition Nuclear-armed states NPT recognizedUnited States Russia United Kingdom France China OthersIndia Israel (undeclared) Pakistan North Korea FormerSouth Africa Belarus Kazakhstan Ukraine vte Nuclear ethics is a...

Faculty of engineering and applied science at Queen's University at Kingston Stephen J. R. Smith Faculty of Engineering and Applied ScienceFormer names Kingston School of Mining (1893–1910) Queen's University Faculty of Applied Science (1910–2010) Queen's University Faculty of Engineering and Applied Science (2010–2023) TypeFacultyEstablished1893 (1893)AffiliationQueen's University at KingstonDeanKevin DeluzioLocationKingston, Ontario, CanadaWebsitesmithengineering.queensu.ca The S...

Voce principale: Modena Football Club. Modena Football ClubStagione 1954-1955Sport calcio Squadra Modena Allenatore Renzo Magli Presidente Alessandro Bonaccini Serie B3º posto. Maggiori presenzeCampionato: Robotti (34) Miglior marcatoreCampionato: Cabas (12) 1953-1954 1955-1956 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Modena Football Club nelle competizioni ufficiali della stagione 1954-1955. Indice 1 Rosa 2 Risultati 2.1 Serie B 2.1.1...

Come leggere il tassoboxRatto delle sabbie minore Stato di conservazione Dati insufficienti[1] Classificazione scientifica Dominio Eukaryota Regno Animalia Sottoregno Eumetazoa Superphylum Deuterostomia Phylum Chordata Subphylum Vertebrata Infraphylum Gnathostomata Superclasse Tetrapoda Classe Mammalia Sottoclasse Theria Infraclasse Eutheria Superordine Euarchontoglires Ordine Rodentia Famiglia Muridae Sottofamiglia Gerbillinae Genere Psammomys Specie P.vexillaris Nomenclatura binomi...

Australian cyclist (born 1989) Glenn O'SheaO'Shea during the Glasgow event of the 2012–2013 UCI Track Cycling World Cup Classics season.Personal informationBorn (1989-06-14) 14 June 1989 (age 34)Swan Hill, VictoriaHeight180 cm (5 ft 11 in)Weight76 kg (168 lb)Team informationDisciplineRoad and trackRoleRiderAmateur teams2009Australian Institute of Sport2013Garmin–Sharp (stagiaire) Professional teams2010–2012Jayco–AIS2013–2014An Post–Chain Reaction2015T...

To the Beautiful YouPromotional posterGenreKomedi romantis DramaDitulis olehLee Young-chulBased on Hana-Kimi byHisaya NakajoSutradaraJun Ki-sangPemeranSulli ChoiChoi MinhoLee Hyun WooLagu pembukaButterfly oleh Jessica Jung dan Krystal JungLagu penutupStand Up oleh J-MinNegara asalKorea SelatanBahasa asliKoreanJmlh. musim1Jmlh. episode16ProduksiLokasi produksiKoreaDurasiRabu & Kamis 21:55 (KST)Rumah produksiS.M. EntertainmentRilis asliJaringanSBSRilis15 Agustus 2012 To The Beautiful You (...

Taiwanese politician Tsai Pi-chung蔡碧仲Official portrait, 2017Political Deputy Minister of JusticeIncumbentAssumed office 25 December 2018Serving with Chen Ming-tangMinisterTsai Ching-hsiangIn office21 November 2016 – 17 September 2018MinisterChiu Tai-sanTsai Ching-hsiangActing Magistrate of HualienIn office17 September 2018 – 25 December 2018Preceded byFu Kun-chiSucceeded byHsu Chen-wei Personal detailsBornSeptember 1958 (age 65)Yuanchang, Yunl...

American politician John Dailey127th Mayor of TallahasseeIncumbentAssumed office November 19, 2018Preceded byAndrew Gillum Personal detailsBornJohn Evans Dailey (1972-12-07) December 7, 1972 (age 51)Miami, Florida, U.S.Political partyDemocraticSpouseVirginia DaileyChildren2EducationFlorida State University, Tallahassee (BA, MPA)London School of Economics (MA) John Evans Dailey (born December 7, 1972) is an American politician from the state of Florida. He is the mayor of Tallahassee,...

Not to be confused with California Academy of Sciences or California Institute of Science. Science museum in California, U.S.California Science CenterEstablished1951; 73 years ago (1951) (as California Museum of Science and Industry)1998; 26 years ago (1998) (as California Science Center)LocationExposition Park, Los Angeles, California, U.S.Coordinates34°0′56″N 118°17′9″W / 34.01556°N 118.28583°W / 34.01556; -118.28583Typ...

Berlin Buckower ChausseeThrough stationThe archway of the Buckower Chaussee stationGeneral informationLocationMarienfelde, Tempelhof-Schöneberg, BerlinGermanyCoordinates52°24′38″N 13°22′58″E / 52.41056°N 13.38278°E / 52.41056; 13.38278Line(s) Berlin–Dresden suburban railway (KBS 200.2) Platforms2Tracks2ConstructionArchitectRainer G. RümmlerOther informationStation code951DS100 codeBBCH[1]IBNR8089010Category5[2]Fare zoneVBB: Berlin B/5656...

Branch of the Northeast Caucasian language family AndicGeographicdistributionDagestanLinguistic classificationNortheast CaucasianAvar–AndicAndicGlottologandi1254 The Andic languages are a branch of the Northeast Caucasian language family. They are often grouped together with the Avar language and (formerly) with the Tsezic (Didoic) languages to form an Avar–Andic (or Avar–Andic–Didoic) branch of that family. Internal branching Schulze (2009)[1] gives the following family tree:...