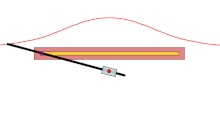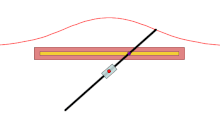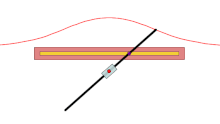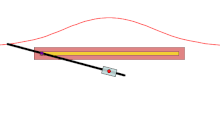
蚌线
|
Read other articles:
Dorysthenes rostratus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Dorysthenes Spesies: Dorysthenes rostratus Dorysthenes rostratus adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Dorysthenes, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada ba...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Upāsaka dan Upāsikā – berita · surat kabar · buku · cendekiawan · JSTORartikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini sema...
For the community in Renfrew County, Ontario, see Admaston/Bromley. Township in Ontario, CanadaMcDougallTownship (single-tier)Township of McDougallMunicipal officeMotto(s): A Great Place To Live, A Great Place To VisitMcDougallCoordinates: 45°27′N 80°01′W / 45.450°N 80.017°W / 45.450; -80.017CountryCanadaProvinceOntarioDistrictParry SoundIncorporatedMay 1, 1872Government • TypeTownship • MayorDale Robinson • Federal ridi...

Academic journalTransactions of the American Philological AssociationDisciplineClassics, philologyLanguageEnglishEdited byCraig GibsonPublication detailsHistory1869–presentPublisherJohns Hopkins University Press (United States)FrequencyBiannuallyStandard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )ISO 4Trans. Am. Philol. Assoc.IndexingCODEN (alt · alt2) · JSTOR (alt) ·...

BMC Invitation 1972 Sport Tennis Data 12 gennaio - 15 gennaio Edizione 2a Superficie Cemento Campioni Singolare Billie Jean King Doppio Rosemary Casals / Virginia Wade 1971 1973 Il BMC Invitation 1972 è stato un torneo di tennis giocato sul cemento. È stata la 2ª edizione del torneo, che fa parte del Virginia Slims Circuit 1972. Si è giocato a San Francisco negli USA dal 12 al 15 gennaio 1972. Indice 1 Campionesse 1.1 Singolare 1.2 Doppio 2 Collegamenti esterni Campionesse Singolare Lo s...

2019 American sitcom Mr. IglesiasGenre Sitcom Created byKevin HenchStarring Gabriel Fluffy Iglesias Sherri Shepherd Jacob Vargas Maggie Geha Richard Gant Cree Cicchino Fabrizio Guido Tucker Albrizzi Theme music composerOzomatliComposerJoseph LoDucaCountry of originUnited StatesOriginal languageEnglishNo. of seasons2 (3 parts)No. of episodes21ProductionExecutive producers Kevin Hench Gabriel Iglesias Ron DeBlasio Joe Meloche Andy Ackerman Peter Murrieta Producers Chris Arrington Isaac Gonzalez...

American chain of pancake houses This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may contain excessive or inappropriate references to self-published sources. Please help improve it by removing references to unreliable sources where they are used inappropriately. (February 2023) (Learn how and when to remove this message) This article may rely excessively on sources too closel...

Halaman ini berisi artikel tentang bentuk modern. Untuk bentuk kuno, lihat Alfabet Yunani Kuno. Alfabet YunaniJenis aksara Alfabet BahasaTerutama bahasa Yunani, dengan modifikasi untuk menuliskan bahasa lainnya.Periodesekitar 800 SM sampai sekarang[1]Arah penulisanKiri ke kananAksara terkaitSilsilahHieroglif MesirAbjad Proto-SinaiAbjad FenisiaAlfabet YunaniAksara turunan Gotik Glagolitik Kiril Koptik Armenia Italik Kuno (Etruria, Latin, Rune) Aksara kerabat Aram Ibrani Kuno Hispania K...

Michael MazePersonal informationNama lengkapMichael MazeKebangsaan DenmarkLahir1 September 1981 (umur 42)Faxe, DenmarkPeringkat tertinggi8 (Januari 2010)[1]Tinggi185 m (606 ft 11+1⁄2 in)[2]Berat71 kg (157 pon; 11,2 st)[2] Rekam medali Mewakili Denmark Putra Tenis meja Olympic Games 2004 Athens Doubles World Championships 2005 Shanghai Singles European Championships 2005 Århus Team 2009 Stuttgart Singles 2009 Stuttga...

Destroyer class of the US Navy USS Barker in 1928 Class overview NameClemson class BuildersVarious Operators United States Navy United States Coast Guard Royal Navy Royal Canadian Navy Soviet Navy Imperial Japanese Navy Preceded byWickes class Succeeded byFarragut class SubclassesTown class Built1918–1922 In service1919–1948 Planned162 Completed156 Cancelled6 (DD-200 to DD-205) Lost20 General characteristics TypeDestroyer Displacement 1,215 tons (n...

Major Hindu scripture Several terms redirect here. For other uses, see Bhagavad Gita (disambiguation) and Gita (disambiguation). Bhagavad GitaBhagavad Gita's revelation: Krishna tells the Gita to ArjunaInformationReligionHinduismAuthorTraditionally attributed to VyasaLanguageSanskritChapters18Verses700Full text The Bhagavad Gita at English Wikisource The Bhagavad Gita (/ˌbʌɡəvəd ˈɡiːtɑː/; Sanskrit: भगवद्गीता, romanized: bhagavad-gītā, lit. ...

English biochemist William AstburyFRSBornWilliam Thomas Astbury(1898-02-25)25 February 1898Longton, EnglandDied4 June 1961(1961-06-04) (aged 63)Leeds, EnglandCitizenshipBritishAlma materUniversity of CambridgeKnown forBeta sheetFiber diffractionX-ray diffraction of DNAAwardsActonian Prize (1935)Croonian Medal (1945)Scientific careerFieldsPhysics, Molecular biologyInstitutionsUniversity College LondonRoyal Institution University of LeedsDoctoral advisorWilliam Henry Bragg[1&...

Sporting event delegationGreece at the2009 World Championships in AthleticsWA codeGRENational federationHellenic Amateur Athletic AssociationWebsitewww.segas.grin BerlinCompetitors21Medals Gold 0 Silver 0 Bronze 0 Total 0 World Championships in Athletics appearances (overview)1983198719911993199519971999200120032005200720092011201320152017201920222023← 2007 2011 → Greece competed with 21 athletes (7 men and 14 women) at the 2009 World Championships in Athletics, 15–23 August 200...

See also: Syrian Democratic Council Politics of Autonomous Administration of North and East Syria Symbols Symbols of Rojava Constitution Libertarian socialism Human rights Legislature and Government Syrian Democratic Council Executive Council Elections March 2015 (Local) September 2017 (Local) December 2017 (Regional) Political parties Democratic Union Party (PYD) Syriac Union Party (SUP) Wheat Wave Movement (QMH) Syrian National Democratic Alliance (SNDA) Honor and Rights Convention (HRC) Y...

Disambiguazione – Se stai cercando altri significati, vedi Stampa (disambigua). Disambiguazione – Stampatore rimanda qui. Se stai cercando lo stampatore d'arte, vedi Stampatore d'arte. Stampa mediante una macchina rotativa. Lettera a stampata su un foglio di carta al microscopio La stampa è un processo per la riproduzione di testi e/o di immagini su di un supporto rigido o semirigido. Attualmente viene realizzata soprattutto mediante l'impiego d' inchiostro su carta e di una pre...

كأس بلغاريا 2002–03 تفاصيل الموسم كأس بلغاريا النسخة 63 البلد بلغاريا التاريخ بداية:9 أكتوبر 2002 المنظم اتحاد بلغاريا لكرة القدم البطل ليفسكي صوفيا كأس بلغاريا 2001–02 كأس بلغاريا 2003–04 تعديل مصدري - تعديل كأس بلغاريا 2002–03 (بالبلغارية: Купа на Бълга�...

2001 EP by Murder City DevilsThelemaEP by Murder City DevilsReleasedSeptember 4, 2001GenrePunk rockLength20:59LabelSub Pop RecordsMurder City Devils chronology In Name and Blood(2000) Thelema(2001) R.I.P.(2003) Thelema is an EP by the Murder City Devils released on September 4, 2001 on Sub Pop Records. It is their last release of entirely original material before they broke up later that year. Spencer Moody has said that it was really my favorite stuff overall.[1] To support t...

Voce principale: Società Sportiva Chieti Calcio. Chieti CalcioStagione 2001-2002Sport calcio Squadra Chieti Allenatore Piero Braglia Presidente Antonio Buccilli Serie C18º posto nel girone B. Maggiori presenzeCampionato: Zattarin (32) Miglior marcatoreCampionato: Biancolino (8) 2000-2001 2002-2003 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti il Chieti Calcio nelle competizioni ufficiali della stagione 2001-2002. Indice 1 Rosa 2 Risultati 2...

Biografi tokoh yang masih hidup ini tidak memiliki referensi atau sumber sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Macaulay Culkin – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Macaulay CulkinMa...
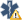
متلازمة الظفر الأصفر متلازمة الظفر الأصفر: مريضه مصابة بوذمة لمفية حادة في كلتا رجليها منذ عشرين عاماً. أظافر الإبهام متعرجة، سميكة، صفراء، ومنحنية وكذا الحال في أظافر إصبعي القدم الكبيرين، وانصباب جنبي ليمفي على الناحيتين. عينة من السائل الذي تم سحبه موضحة على الجانب ال�...














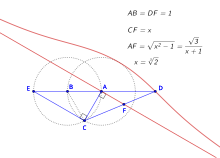
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)























![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)






























![{\displaystyle \therefore KG={\sqrt[{3}]{2}}GH}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ec34086c4ef9bafb7b98941cdf23c054871eeb)