Четырёхмерный многогранник
| ||||||||||||||||||||||||||||||
Read other articles:

1532 battle during the Spanish conquest of the Inca Empire Capture of AtahualpaPart of the Spanish conquest of PeruPainting by Juan Lepiani depicting the capture of Atahualpa in Cajamarca.DateNovember 16, 1532LocationCajamarca, PeruResult Spanish victory Capture of Atahualpa Fall of the Inca EmpireBelligerents Spanish Empire Incas faithful to AtahualpaCommanders and leaders Francisco Pizarro Hernando Pizarro Hernando de Soto Atahualpa (POW)Strength 106 infantry62 cavalry four cannons12 h...

Medical conditionNeonatal jaundiceOther namesNeonatal hyperbilirubinemia, neonatal icterus, jaundice in newbornsJaundice in a newbornSpecialtyPediatricsSymptomsYellowish discoloration of the skin and white part of the eyes[1]ComplicationsSeizures, cerebral palsy, kernicterus[1]Usual onsetNewborns[1]TypesPhysiologic, pathologic[1]CausesRed blood cell breakdown, liver disease, infection, hypothyroidism, metabolic disorders[2][1]Diagnostic methodB...

A. Joko Takarianto Pa Sahli Tk. III Bidang Intekmil dan Siber Panglima TNIMasa jabatan17 Juli 2023 – 2 Oktober 2023 PendahuluHesly PaatPenggantiDanang Hadiwibowo Informasi pribadiLahir12 November 1965 (umur 58)Cimahi, Jawa BaratAlma materAkademi Angkatan Udara (1988)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan UdaraMasa dinas1988–2023Pangkat Marsekal Muda TNISatuanKorps PenerbangPertempuran/perangKonflik PapuaSunting kotak info • L • B Marse...

Spanish politician In this Spanish name, the first or paternal surname is Tertsch and the second or maternal family name is del Valle-Lersundi. Hermann TertschTertsch in 2022Member of the European ParliamentIncumbentAssumed office 2 July 2019ConstituencySpain Personal detailsBornHermann Leopoldo Tertsch y del Valle de Lersundi (1958-04-09) 9 April 1958 (age 66)Madrid, SpainPolitical partyVox (2019–present)Other politicalaffiliationsPCE-EPK (1977)Children1Parent(s)Ekkehard T...

Book by Ion Idriess Headhunters of the Coral Sea Original coverAuthorIon IdriessCountryAustraliaLanguageEnglishGenrejuvenile literaturePublisherAngus and RobertsonPublication date1940 Headhunters of the Coral Sea is a 1940 book by Ion Idriess about Jack Ireland and Will d'Oyly, two survivors of the 1834 wreck, the Charles Eaton.[1] Idriess had previously written a version of this story in Drums of Mer. References ^ Adventure Stories With Settings Round Australia. The Mail (Adelaide). ...

Flag of the governor The governor of North Dakota is the head of government of the U.S. state of North Dakota. The governor is the head of the executive branch of North Dakota's state government and is charged with enforcing state laws. There have been 32 governors since North Dakota became a state, serving 33 distinct terms, with William Langer having been elected to multiple terms. The current officeholder is Republican Doug Burgum. Governors For governors before statehood, see List of gov...

Epic Mickey 2: L'avventura di Topolino e OswaldvideogiocoTitolo originaleEpic Mickey 2: The Power of Two (NA)Epic Mickey: The Power of 2 (EU) PiattaformaWii, Wii U, PlayStation 3, Xbox 360, PlayStation Vita, Microsoft Windows Data di pubblicazioneWii: 26 settembre 2013 18 novembre 2012 23 novembre 2012 22 novembre 2012 Wii U: 26 settembre 2013 18 novembre 2012 30 novembre 2012 13 dicembre 2012 PlayStation 3, Xbox 360: 18 novembre 2012 23 novembre 2012 22 novembre 2012 Play...

1893 book by Émile Durkheim Cover of a French edition of The Division of Labour in Society The Division of Labour in Society (French: De la division du travail social) is the doctoral dissertation of the French sociologist Émile Durkheim, published in 1893. It was influential in advancing sociological theories and thought, with ideas which in turn were influenced by Auguste Comte. Durkheim described how social order was maintained in societies based on two very different forms of solidarity...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Jaffna යාපනය யாழ்ப்பாணம் Rue de Jaffna en 2011 Administration Pays Sri Lanka Province Province du Nord District District de Jaffna Maire Yogeswari Patkunarajah Parti politique : EPDPAlliance : UPFA Démographie Population 88 138 hab. (2012) Densité 4 363 hab./km2 Population de l'agglomération 583 378 hab. Densité 569 hab./km2 Géographie Coordonnées 9° 40′ 00″ nord, 80° 00′ 00″...

Rank comparison chart of officers for navies of African states. Officers Rank group General/flag officers Senior officers Junior officers Officer cadet Algerian National Navy[1]vte فريق أولFariq 'awal فريقFariq لواءLiwa عميدAmid عقيدAqid مقدمMuqaddam رائدRa'id نقيبNaqib ملازم أولMulazim awwal ملازمMulazim Général d'armée Général de corps d'armée Général de division Général Colonel Lieutenant-colonel Commandant Capit...

Carrot puddingCarrot pudding with fruitsTypePuddingMain ingredientscarrots, butter, sugar, eggs, spices Carrot pudding is a dish traditional to a wide range of cultures around the world. It can be served either as a savoury pudding (as an accompaniment to a regular meal) or as a sweet dessert. An English recipe, published in 1591, describes pudding in a Carret [sic] root[1] that is essentially a stuffed carrot with meat, shortening, cream, eggs, raisins, sweetener (dates ...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: El Gamaliya – news · newspapers · books · scholar · JSTOR (January 2022) City in Dakahlia, EgyptEl Gamaliya الجماليهCityEl GamaliyaLocation in EgyptCoordinates: 31°10′50″N 31°51′55″E / 31.18056°N 31.86528°E ...

Coppa LombardiaSport Calcio TipoClub Paese Italia OrganizzatorePierino Negrotto Cambiaso AperturaVariabile ChiusuraVariabile FormulaChallenge round StoriaFondazione1904 Soppressione1922 Detentrice Genoa Ultimo vincitore Genoa Modifica dati su Wikidata · Manuale La Coppa Lombardia era un trofeo calcistico per squadre di club istituito nei primi anni del XX secolo. Il trofeo fu messo in palio a proprie spese da Pierino Negrotto Cambiaso, presidente del Casteggio. Il trofeo ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Indian pie – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) A Bhopal State postage stamp worth 1 anna and three pies A pie (abbreviated as Ps) was a unit of currency in India, Burma and Pakistan until 194...

Pour les articles homonymes, voir Prix Napoli. Le Prix de la Ville de Naples (en italien Gran Premio Citta' di Napoli) rebaptisé Gran Premio Franco Antonio e Salvio Cervone en 2021, est une course hippique de trot attelé se déroulant au mois de juin (début juillet en 2016 et 2023, fin mai en 2021) sur l'hippodrome d'Agnano à Naples (Italie). C'est une course de Groupe I réservée aux chevaux de 3 ans. Elle se court sur la distance de 2 100 mètres, avec un départ à l'autost...

Military units trained to conduct special operations Special Operations Forces redirects here. For other uses, see Special Operations Force (Singapore), Special Operations Forces (Russia), and Special Operations Forces (Ukraine). Crack-troops redirects here. For the military formation, see Shock troops. For other uses, see Special forces (disambiguation) and Elite Force (disambiguation). An American special forces team moves together out of an U.S. Air Force CV-22 Osprey aircraft on February ...

きほうちょう 紀宝町 道の駅紀宝町ウミガメ公園のウミガメプール 紀宝町旗 紀宝町章 国 日本地方 東海地方、近畿地方都道府県 三重県郡 南牟婁郡市町村コード 24562-3法人番号 1000020245623 面積 79.62km2総人口 9,740人 [編集](推計人口、2024年8月1日)人口密度 122人/km2隣接自治体 熊野市、南牟婁郡御浜町和歌山県新宮市町の木 ウバメガシ町の花 カンラン、スイセン紀宝�...
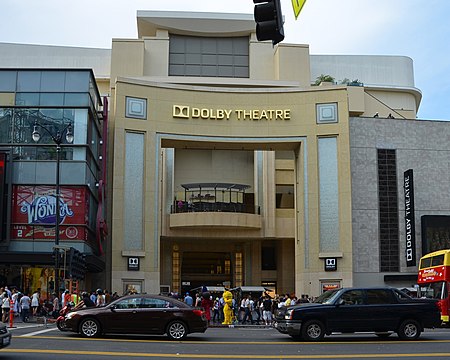
Il Dolby Theatre a Hollywood La 95ª edizione dei premi Oscar si è tenuta a Los Angeles al Dolby Theatre il 12 marzo 2023 ed è stata presentata da Jimmy Kimmel, che torna alla conduzione del celebre evento per la terza volta dopo le edizioni del 2017 e 2018.[1] Le candidature sono state annunciate il 24 gennaio 2023. Il 21 giugno 2022 sono stati annunciati i vincitori del premio Oscar onorario e del premio umanitario Jean Hersholt[2] che sono stati consegnati durante la ceri...

Village development committee in Mahakali Zone, NepalGajari गाजरीVillage development committeeGajariLocation in NepalCoordinates: 29°28′N 80°43′E / 29.46°N 80.72°E / 29.46; 80.72CountryNepalZoneMahakali ZoneDistrictBaitadi DistrictPopulation (1991) • Total3,190 • ReligionsHinduTime zoneUTC+5:45 (Nepal Time) Gajari is a village development committee in Baitadi District in the Mahakali Zone of western Nepal. At the time of t...















