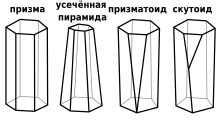
Скутоид
|
Read other articles:

Untuk struktur habitat fiksi di luar angkasa, lihat Stasiun dan habitat antariksa dalam budaya masyarakat. Pemandangan luar torus Stanford. Di bawah tengah terdapat cermin matahari primer statik yang memantulkan sinar matahari ke cincin cermin sekunder melengkung di sekitar penghubung. Lukisan karya Donald E. Davis Interior torus Stanford. Lukisan karya Donald E. Davis Torus Stanford adalah usulan desain[1] habitat antariksa yang mampu menampung 10.000 sampai 140.000 penduduk permanen...

Basel GhattasLahir23 Maret 1956 (umur 67)Tempat lahirNazareth, IsraelKnesset19, 20Faksi yang diwakili di Knesset2013–2015Balad2015–2017Joint List Dr Basel Ghattas (Arab: باسل غطاسcode: ar is deprecated , Ibrani: באסל גטאס; lahir 23 Maret 1956) adalah seorang politikus Arab Israel. Seorang anggota Balad, ia menjabat sebagai anggota Knesset untuk Balad dan Joint List dari 2015 sampai 2017. Pranala luar Basel Ghattas di situs web Knesset

جيم بيرنز (بالإنجليزية: Jim Burns) معلومات شخصية اسم الولادة (بالإنجليزية: James B. Burns) الميلاد 21 سبتمبر 1945 ماكلينسبورو تاريخ الوفاة 11 ديسمبر 2020 (75 سنة) [1] الطول 190 سنتيمتر[2] مركز اللعب هجوم خلفي الجنسية الولايات المتحدة الوزن 88 كيلوغرام المد...

У этого термина существуют и другие значения, см. P. Буквы со сходным начертанием: Ρ · ρ · Р · р Буква латиницы P Pp Изображение ◄ L M N O P Q R S T ► ◄ l m n o p q r s t ► Характеристики Название P: latin capital letter pp: latin small letter p Юникод P: U+0050p: U+0070 HTML-...

Station of the Tehran Metro Javadiyeh Metro Stationایستگاه مترو جوادیهTehran Metro StationGeneral informationLocationJavadiyeh, Districts 11-16, Tehran, Tehran CountyTehran Province, IranOperated byTehran Urban and Suburban Railways Organization (Metro)Connections Tehran BRT BRT 4 HistoryOpened2 Ordibehesht 1393 H-Sh (22 April 2014)[1]Services Preceding station Tehran Metro Following station Rahahantowards Ghaem Zam Zamtowards Azadegan Javadiyeh Metro Stat...

For other uses, see Subcetate (disambiguation). For Sub Cetate village in the same county, see Zetea. Commune in Harghita, RomaniaSubcetateCommune Coat of armsLocation in Harghita CountySubcetateLocation in RomaniaCoordinates: 46°51′N 25°26′E / 46.850°N 25.433°E / 46.850; 25.433CountryRomaniaCountyHarghitaGovernment • Mayor (2020–2024) Vasile Rusu (PSD)Area51.11 km2 (19.73 sq mi)Elevation712 m (2,336 ft)Population ...

Japanese politician Shirane Sen’ichi白根専一Shirane Sen’inchiBorn(1850-02-03)February 3, 1850Hagi, Chōshū Domain, JapanDiedJune 14, 1898(1898-06-14) (aged 48)Tokyo, JapanNationalityJapaneseOccupation(s)politician, cabinet minister In this Japanese name, the surname is Shirane. Baron Shirane Sen'ichi (白根専一, February 3, 1850 – June 14, 1898) was a politician and bureaucrat in Meiji period Empire of Japan. In 1907, he was raised to the rank and title of danshaku (baron) ...

Halaman pembuka The Wife of Bath's Tale. The Wife of Bath's Tale (bahasa Inggris Pertengahan: The Wyves Tale of Bathe) adalah salah satu dari kisah dalam The Canterbury Tales karya Geoffrey Chaucer. The Wife of Bath's Tale berkisah mengenai ksatria di istana Raja Arthur yang memperkosa seorang perempuan di ladang gandum. Menurut hukum, ia harus dihukum mati, tetapi sang ratu menjadi pengantara, dan menghukum sang ksatria dengan menyuruhnya pergi mencari jawaban dari pertanyaan apa yang pa...

2016 single by Selah Sue featuring Childish GambinoTogetherSingle by Selah Sue featuring Childish Gambinofrom the album Reason ReleasedFebruary 22, 2016GenrePopelectropoptrapLength3:21LabelBecause MusicSongwriter(s)Evan Kidd BogartDonald GloverLudwig GoranssonSanne PutseysProducer(s)Ludwig GoranssonSelah Sue singles chronology Fear Nothing (2015) Together (2016) Bang Bang (2016) Childish Gambino single singles chronology Sober(2014) Together(2016) Me and Your Mama(2016) Together is a ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: National Institute of Nursing Research – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) National Institute of Nursing Research (NINR)Agency overviewJurisdictionFederal Government of the United StatesAgency ex...

The Married VirginIklan dari The Moving Picture WorldSutradaraJoe MaxwellSkenarioHayden TalbotCeritaHayden TalbotPemeranVera SissonRodolfo di ValentinaFrank NewburgKathleen KirkhamEdward JobsonLillian LeightonPenata musikBrian Benison (new score 2000)PerusahaanproduksiMaxwell ProductionsDistributorGeneral Film CompanyTanggal rilis Desember 1918 (1918-12) Durasi71 menitNegaraAmerika SerikatBahasaAntarjudul Inggris Valentino dalam sebuah iklan untuk film tersebut. The Married Virgin ...

جراند ثفت أوتو: ذا لوست أند دامد (بالإنجليزية: Grand Theft Auto IV: The Lost and Damned) المطور روكستار نورث[ا] الناشر روكستار جيمز الموزع تيك-تو إنترأكتيف الكاتب دان هاوسرRupert Humphries سلسلة اللعبة جي تي أي محرك اللعبة RAGE[2] النظام مايكروسوفت ويندوز، بلاي ستيشن 3، إكس بوكس 360 تاریخ ال...

International cricket tour Kenyan cricket team in Sri Lanka in 2001–02 Sri Lanka A KenyaDates 26 January – 25 February 2002Captains Upul Chandana Maurice OdumbeFC seriesResult Sri Lanka A won the 3-match series 3–0Most runs Upul Chandana (279)[1] Steve Tikolo (314)[1]Most wickets Upul Chandana (18)[2] Collins Obuya (11)[2]LA seriesResult Kenya won the 3-match series 2–1Most runs Upul Chandana (180)[3] Ravindu Shah (154)[3&#...

Cet article est une ébauche concernant les probabilités et la statistique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Pearson. Les fonctions de Pearson ont été créées pour représenter des distributions unimodales. Il en existe douze. Elles ont été inventées par Karl Pearson à la fin du XIXe siècle et au début du XXe siècle. Historique Le système de ...

Титульный лист французской Энциклопедии Дидро и Д’Аламбера Эпо́ха Просвеще́ния[1], Эпоха «просвещения»[2] — одна из ключевых эпох (периода «долгого XVIII века»[3]) в истории европейской культуры, связанная с развитием научной, философской и общественной мысл...

Pangkat Polri Perwira Jenderal Polisi Komisaris Jenderal Polisi Inspektur Jenderal Polisi Brigadir Jenderal Polisi Komisaris Besar Polisi Ajun Komisaris Besar Polisi Komisaris Polisi Ajun Komisaris Polisi Inspektur Polisi Satu Inspektur Polisi Dua Bintara dan Tamtama Ajun Inspektur Polisi Satu Ajun Inspektur Polisi Dua Brigadir Polisi Kepala Brigadir Polisi Brigadir Polisi Satu Brigadir Polisi Dua Ajun Brigadir Polisi Ajun Brigadir Polisi Satu Ajun Brigadir Polisi Dua Bhayangkara Kepala Bhay...

Voce principale: Dialetto lombardo occidentale. Una carta, opera di Gaetano Crespi, che riporta i luoghi di influenza culturale del milanese ed alcuni sottodialetti ivi compresi (da Fontana 1901: XXXV) Per letteratura milanese (o meneghina) si intende, di norma, la letteratura prodotta a Milano e nelle località limitrofe, usando quella varietà di lingua lombarda che ha nel milanese il rappresentante di riferimento. I limiti di questo ambito letterario si possono tracciare solo in modo appr...

فيبسيونعلم الفيبسيينالتعداد الكليالتعداد ~6,000مناطق الوجود المميزة روسيا 5,936 (2010) أوكرانيا 281 (2001) إستونيا 54 (2011) بيلاروسيا 8 (2009)اللغات لغة روسية، لغة فيبسيةاللغة الأم الفيبسية الدين الكنيسة الروسية الأرثوذكسيةالمجموعات العرقية المرتبطةفرع من شعوب فنلندية أوغري�...

Sepatu adalah salah satu jenis alas kaki (footwear) yang biasanya terdiri atas bagian-bagian sol, hak, kap, tali, dan lidah. Biasanya juga terbuat dari kanvas atau kulit yang menutupi semua bagian mulai dari jari jemari, punggung kaki hingga bagian tumit yang difungsikan untuk [1]melindungi kaki dari kotoran berupa debu, kerikil, atau bahkan lumpur dan puing. Pengelompokkan sepatu biasanya dilakukan berdasarkan fungsi atau tipenya, seperti sepatu resmi (pesta), sepatu santai (kasual),...

معركة بروزة جزء من الحرب العثمانية - البندقية (1537 - 1540) خير الدين بربروس يهزم العصبة المقدسة (1538م) بقيادة أندريا دوريا في معركة بروزة معلومات عامة التاريخ 28 سبتمبر 1538 الموقع بريفيزا (البحر الأيوني)38°57′33″N 20°45′01″E / 38.9592°N 20.7503°E / 38.9592; 20.7503 النتيجة نصر حاسم للع...