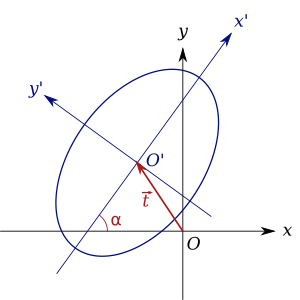
Matrix representation of conic sections
|
Read other articles:

Gunung LewotobiPemandangan Pulau Konga dan gunung berapi ganda Lewotobi, yang terdiri dari Perampuan dan Laki-Laki, circa 1915Titik tertinggiKetinggian1.584 m / 5.196 kaki (Gn. Lewotobi Laki-Laki)1.703 m / 5.587 kaki (Gn. Lewotobi Perempuan)Koordinat8°32′00″S 122°45′28″E / 8.5333115°S 122.7579122°E / -8.5333115; 122.7579122Koordinat: 8°32′00″S 122°45′28″E / 8.5333115°S 122.7579122°E / -8.5333115; 122.7579122 Geograf...

Pemandangan Pulau Ellaidhoo dan Bathaala dari udara Ellaidhoo (Divehi : އެއްލައިދޫ) adalah sebuah pulau kecil yang merupakan bagian dari Atol Alif Alif di negara Maladewa. Ellaidhoo merupakan salah satu pulau di Maladewa yang telah disulap menjadi hotel untuk wisatawan sejak tahun 1985, dan hotel ini disebut Ellaidhoo Maldives Resort[1] Geografi Ellaidhoo terletak di Maladewa tengah, tepatnya di sebelah timur atoll Ari, dan masuk ke dalam wilayah administratif Alif Alif...

Britannia menawarkan pengampunan dan janji kompensasi untuk Loyalis terusir kelahiran Amerika. (Reception of the American Loyalists by Great Britain in the Year 1783. Engraving by H. Moses after Benjamin West.) Loyalis adalah para kolonis Amerika yang masih setia kepada Kerajaan Britania Raya (dan raja Britania) selama Perang Revolusi Amerika. Mereka sering disebut Tories, Royalists, atau King's Men oleh Patriot, yaitu orang-orang yang mendukung revolusi. Jika Loyalis dikalahkan, sekitar 20% ...

Albert L. Gutterson FieldhouseThe GutGutterson Fieldhouse interior in March 2023LocationBurlington, VermontOwnerUniversity of VermontOperatorUniversity of VermontCapacity4,035 (ice hockey)Surface200 x 90 ft (ice hockey)ConstructionBroke ground1961Opened1963ArchitectFreeman French Freeman[1]TenantsVermont Catamounts (NCAA)Men's ice hockey (1963–present)Women's ice hockey (1998–present)Vermont Bucks (Can-Am) (2017) Gutterson Fieldhouse (nicknamed The Gut[2]) is a 4,0...

Sumitomo Mitsui Financial GroupJenisPublikKode emitenTYO: 8316NYSE: SMFGIndustriJasa KeuanganDidirikan2002KantorpusatTokyo, JepangTokohkunciTeisuke Kitayama (Presiden)Pendapatan ¥3,073 triliun (2011)[* 1]Laba bersih ¥550.84 milyar (2011)[* 1]Total aset ¥131.48 triliun (2011)[* 1]Total ekuitas ¥5,303 triliun (2011)[* 1]Karyawan62.379 (2011)[* 1]AnakusahaSumitomo Mitsui Banking CorporationSitus webhttp://www.smfg.co.jp/ Sumitomo Mitsui Financial Group...

Mostowfi ol-Mamalek Perdana Menteri IranMasa jabatan15 Juli 1910 – 19 Juli 1911Penguasa monarkiAhmad Shah QajarPendahuluVosough od-DowlehPenggantiVosough od-DowlehMasa jabatan1 Juli 1914 – 1 Februari 1915Penguasa monarkiAhmad Shah QajarPendahuluMirza Mohammed Ali KhanPenggantiAbdol-Hossein Mirza FarmanfarmaMasa jabatan18 Agustus 1915 – 25 Desember 1915Penguasa monarkiAhmad Shah QajarPendahuluAbdol Majid MirzaPenggantiAbdol-Hossein Mirza FarmanfarmaMasa jabatan...

Prosecution service of South Korea This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this message) This article may be weighted too heavily toward only o...

Not to be confused with Diffeology. In mathematics, a diffiety (/dəˈfaɪəˌtiː/) is a geometrical object which plays the same role in the modern theory of partial differential equations that algebraic varieties play for algebraic equations, that is, to encode the space of solutions in a more conceptual way. The term was coined in 1984 by Alexandre Mikhailovich Vinogradov as portmanteau from differential variety.[1] Intuitive definition In algebraic geometry the main objects of stu...

Voce principale: Calcio Como. Associazione Calcio ComoStagione 1956-1957Sport calcio Squadra Como Allenatore Hugo Lamanna Presidente Francesco Ambrosoli Serie B7º posto Maggiori presenzeCampionato: Bellini, Cuttica, Marsili (32) Miglior marcatoreCampionato: Baldini (11) 1955-1956 1957-1958 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Como nelle competizioni ufficiali della stagione 1956-1957. Indice 1 Stagione 2 Divise...

Antoine de Caunes presentatore della cerimonia La cerimonia di premiazione della 24ª edizione dei Premi César si è svolta il 6 marzo 1999 al Théâtre des Champs-Élysées di Parigi. È stata presieduta da Isabelle Huppert e presentata da Antoine de Caunes. È stata trasmessa da Canal+.[1][2][3] Il film che ha ottenuto il maggior numero di candidature (dodici) è stato Place Vendôme di Nicole Garcia, mentre i film che hanno vinto il maggior numero di premi (tre) so...

Water-polo aux Jeux olympiques de 1912 Généralités Sport Water-polo Éditions 4e Lieu(x) Stockholm Participants 6 équipes Épreuves 1 Palmarès Tenant du titre Grande-Bretagne Vainqueur Grande-Bretagne Deuxième Suède Troisième Belgique Navigation Londres 1908 Anvers 1920 modifier Le tournoi de water-polo aux Jeux olympiques de 1912 ont lieu pendant les épreuves olympiques à Stockholm, en Suède. Équipes 45 poloïstes appartenant à 6 nations participèrent a...

English politician Gareth RobertsAMRoberts in 2020Member of the London Assembly for South WestIncumbentAssumed office 4 May 2024Preceded byNicholas RogersMajority16,019 Personal detailsBorn (1971-03-28) 28 March 1971 (age 53)NationalityEnglishPolitical partyLiberal DemocratsSpousePetra Chantal RobertsChildren3Alma materSt Mary's University, TwickenhamOccupationMarket ResearchProfessionPolitician Gareth David Roberts is a British Liberal Democrat politician, serving as the Member of t...

Patterson HoodPatterson Hood, 2022Background informationBorn (1964-03-24) March 24, 1964 (age 60)Muscle Shoals, AlabamaUnited StatesGenres Southern rock country rock rock and roll Occupation(s)MusiciansongwriterInstrument(s)VocalsguitarYears active1984–presentLabels ATO Records MapleMusic Recordings New West Records Websitepattersonhood.comMusical artist Patterson David Hood (born March 24, 1964) is an American singer-songwriter and co-founder of the band Drive-By Truckers. Early life...

جمعية كشافة النيجر الدولة النيجر تعديل مصدري - تعديل جمعية كشافة النيجر هي المنظمة الكشفية الوطنية في النيجر.[1][2] وقد تأسست في عام 1993 وأصبحت عضوا في المنظمة العالمية للحركة الكشفية في عام 1996. وتعتبر الجمعية مختلطة ولديها 3202 عضوا اعتبارا من عام 2011. روابط خارج�...

Practice of throwing a coin in the air to choose between two alternatives Flipping a coin and Heads or tails redirect here. For the song by Billlie, see The Billage of Perception: Chapter One. For other uses, see Heads or Tails (disambiguation). For Heads and Tails, see Heads and Tails. For coin tossing in cricket, see Toss (cricket). Tossing a coin Coin flipping, coin tossing, or heads or tails is the practice of throwing a coin in the air and checking which side is showing when it lands, in...

Sisa kompor lapisan lemak di Smeerenburg Pemukiman Smeerenburg di Pulau Amsterdam di Svalbard barat daya, berasal dari penangkap paus dari Belanda sebelum 1620: salah satu pengawal luar Eropa yang paling utara. Selama fase intensif pertama dari perikanan paus Spitsbergen, Smeerenburg ialah tempat operasi di utara. (Secara harfiah Smeerenburg, dalam bahasa Belanda berarti kota lapisan lemak). Sekitar 1660, dengan berkurangnya penangkapan paus, pemukiman itu ditinggalkan. Pada 1973 reruntuhan S...

Metro station in Tianjin, China Haiguangsi海光寺General informationOther namesHaiguang TempleLocationNankai District, TianjinChinaOperated byTianjin Metro Co. Ltd.Line(s) Line 1ConstructionStructure typeUnderground and ElevatedHistoryOpened12 June 2006Services Preceding station Tianjin Metro Following station Anshandaotowards Donggulu Line 1 Erweilutowards Liuyuan Haiguangsi Station (Chinese: 海光寺站), literally Haiguang Temple Station in English, is a...

Latin root of the word republic This article is about the Latin phrase. For other uses, see Res publica (disambiguation). This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Res publica – news · newspapers · books · scholar · JSTOR (April 2021) (Learn how and when to remove this message) Part of the Politics seriesRepublicanism Concepts Anti-monarchism Anti...

Romanian footballer This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Stanislau Konrad – news · newspapers · books · scholar · JSTOR (January 2016) Stanislau KonradPersonal informationDate of birth (1913-10-23)23 October 1913Place of birth PolandDate of death 2 February 2000(2000-02-02) (aged 86...

English musicologist (born 1945) David Fallows in 2002 David Fallows (born 20 December 1945) is an English musicologist specializing in music of the late Middle Ages and early Renaissance, as well as the performance practice of music. He is a leader in fifteenth-century music studies, particularly secular song, Guillaume Dufay, and Josquin des Prez, both the subject of landmark biographies Fallows has written. Biography Fallows was born in Buxton on 20 December 1945. He received his BA from J...































![{\displaystyle \nabla Q=\left[{\frac {\partial Q}{\partial x}},{\frac {\partial Q}{\partial y}}\right]=[0,0].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c2d5dcd5abe1ed87051fb34a4ef8a0d5473170)