Alternant matrix
|
Read other articles:

Jung Man-sikLahir11 Desember 1974 (umur 49)Korea SelatanPekerjaanAktorAgenBrave EntertainmentNama KoreaHangul정만식 Alih AksaraJeong Man-sikMcCune–ReischauerChŏng Man-sik Jung Man-sik (Hangul: 정만식; lahir 11 Desember 1974) adalah aktor asal Korea Selatan.[1][2] Filmografi Film Smells Like the Gun (2001) The Little Girl (film pendek, 2003) She's on Duty (2005) Princess Aurora (2005) No Mercy for the Rude (2006) Soo (2007) Paradise Murdered (2007) Textu...
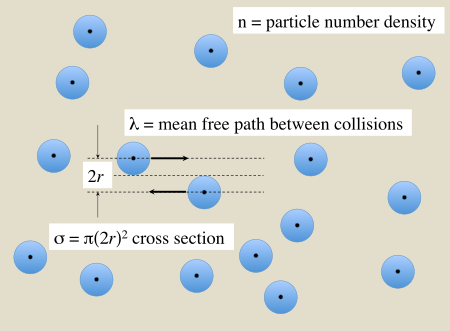
Diagram yang menunjukkan konsep penampang lintang Dalam fisika, penampang lintang (atau tampang-lintang) adalah suatu ukuran peluang terjadinya suatu reaksi (seperti fisi nuklir) terhadap sebuah inti atom atau partikel subatom akibat tabrakan dari partikel lain. Penampang lintang dinyatakan dengan ukuran luas, dalam artian jika partikel penabrak mengenai penampang lingkaran yang memiliki luas tersebut, berposisi tegak lurus dengan jalurnya dan berpusat pada lokasi partikel target, maka reaksi...

Clear-channel news/talk radio station in Sacramento, California KFBKSacramento, CaliforniaBroadcast areaSacramento–Stockton, CaliforniaFrequency1530 kHzBrandingNews 93.1 KFBKProgrammingFormatNews–talkAffiliations ABC News Radio CBS News Radio Compass Media Networks Premiere Networks OwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsKBEBKFBK-FMKHYLKSTEKYRVKZISHistoryFirst air dateSeptember 17, 1922; 101 years ago (1922-09-17)Technical information[1]...

Halaman ini berisi artikel tentang perusahaan media Filipina. Untuk jaringan televisi bernama sama, lihat GMA Network. GMA Network Inc.JenisPublikKode emitenPSE: GMA7IndustriMedia massaPendahuluLoreto F. de Hemedes Inc. (1950-1974)Republic Broadcasting System Inc. (1974–1996)Didirikan14 Juni 1950; 73 tahun lalu (1950-06-14)PendiriRobert Uncle Bob StewartKantorpusatGMA Network CenterEDSA corner Timog Avenue, Brgy. South Triangle, Diliman, Quezon City, FilipinaWilayah operasiSeluruh duni...

Political party in Poland You can help expand this article with text translated from the corresponding article in Polish. Click [show] for important translation instructions. View a machine-translated version of the Polish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English ...

Scenic and historic site in Hunan Province, China This article is about the historic site. For the district, see Wulingyuan District. WulingyuanUNESCO World Heritage SiteThe sandstone pillars of Wulingyuan extend hundreds of meters over the valley floorOfficial nameWulingyuan Scenic and Historic Interest AreaLocationWulingyuan District, Zhangjiajie, Hunan, ChinaCriteriaNatural: (vii)Reference640Inscription1992 (16th Session)Area26,400 ha (102 sq mi)Coordinates29°20�...

Pour l'article sur le World Health Organisation (WHO), voir l’article Organisation mondiale de la santé. The Who The Who en concert en 1975. De gauche à droite : Roger Daltrey, John Entwistle, Keith Moon et Pete Townshend.Informations générales Autre nom The High Numbers Pays d'origine Royaume-Uni Genre musical Hard rock Rock Art rock Opéra-rock Rock psychédélique Garage rock Protopunk Power pop Années actives 1964–198319851988–1989Depuis 1996 Labels DeccaLondonMCA Polydor...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Kitamatsuura District in Nagasaki Prefecture Kitamatsuura (北松浦郡, Kitamatsuura-gun) is a district located in Nagasaki Prefecture, Japan. As of August 1, 2011, the district has an estimated population of 16,270 and a density of 282 persons per km2. The total area is 57.76 km2. Towns and villages Ojika Saza Mergers On April 1, 2005, the towns of Sechibaru and Yoshii merged into the city of Sasebo. On October 1, 2005, the towns of Ikitsuki and Tabira, and the village of Ōshima merge...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

دورة الألعاب العربية 2023 الجزائر دورة الألعاب العربية 2023دورة الألعاب العربية 2023 الدول المشاركة 22 انطلاق الألعاب 5 يوليو 2023 الملعب ملعب 5 جويلية 1962 الاختتام 15 يوليو 2023 الموقع الرسمي الألعاب العربية 2023 دورة الألعاب العربية 2011 تعديل مصدري - تعديل دورة الألعاب ال�...

French novelist and art critic (1848–1907) Joris–Karl HuysmansHuysmans, c. 1895BornCharles-Marie-Georges Huysmans(1848-02-05)5 February 1848Paris, FranceDied12 May 1907(1907-05-12) (aged 59)Paris, FranceOccupationNovelistGenreFictionLiterary movementDecadentNotable worksÀ rebours (1884) Là-bas (1891) En route (1895) La cathédrale (1898)Signature Charles-Marie-Georges Huysmans (US: /wiːsˈmɒ̃s/,[1] French: [ʃaʁl maʁi ʒɔʁʒ ɥismɑ̃s]; 5 February 1848...

الإمبراطورية البابلية الحديثة الإمبراطورية البابلية الحديثة 626 ق.م. – 539 ق.م. خريطة الأمبراطورية البابلية عاصمة بابل نظام الحكم ملكية اللغة الرسمية الأكدية الديانة الديانة البابلية ملوك بابل نبوبولاسر (الأول) 626–605 ق.م. نبو نيد (الأخير) 556–539 ق.م. التاريخ الثورة الب�...

إنديبيندنس الإحداثيات 37°13′42″N 95°42′41″W / 37.2283°N 95.7114°W / 37.2283; -95.7114 [1] تاريخ التأسيس 1869 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة مونغومري عاصمة لـ مقاطعة مونغومري خصائص جغرافية المساحة 19.72741 كيلومت�...

Este artículo o sección se encuentra desactualizado.La información suministrada ha quedado obsoleta o es insuficiente.Este aviso fue puesto el 4 de julio de 2024. Para otros usos de este término, véase Estado Mayor Conjunto. Emblema del Estado Mayor Conjunto El Estado Mayor Conjunto o Junta de Jefes de Estado Mayor (en inglés: Joint Chiefs of Staff, abreviado JCS) es un grupo que comprende a los jefes de Estado mayor de las principales ramas de las Fuerzas Armadas de los Estados Unidos...

German actor (1882–1945) Harry LiedtkeBorn(1882-10-12)12 October 1882Königsberg, East Prussia, German EmpireDied28 April 1945(1945-04-28) (aged 62)Bad Saarow-Pieskow, Nazi GermanyOccupationActorYears active1908–1944Spouses Ernestine Emaline Johanne Proft (m. 1907; div. 1916)[1] Käthe Dorsch (m. 1920; div. 1928) Christa Tordy (m. 1928) P...

Pour les articles homonymes, voir Lin. Dans ce nom chinois, le nom de famille, Lin, précède le nom personnel. Lin Biao Lin Biao en septembre 1955. Fonctions Premier vice-président du Parti communiste chinois 28 avril 1969 – 13 septembre 1971 (2 ans, 4 mois et 16 jours) Président Mao Zedong Prédécesseur Liu Shaoqi (indirectement) Successeur Hua Guofeng (indirectement) Premier vice-Premier ministre du Conseil des affaires de l'État de la république populaire de Chi...

Articulated locomotive with compound steam power Diagram of Mallet articulation (red line) system A typical European Mallet type, a narrow gauge 0-4-4-2 tank locomotive for a mountain railway, the RhB G 2/2+2/3 in Switzerland A 2-10-10-2 Mallet locomotive in Winslow, Arizona, in 1913–14 A Mallet locomotive is a type of compound articulated steam locomotive, invented by the Swiss engineer Anatole Mallet (1837–1919). The front of the locomotive is articulated on a bogie. The compound s...

Disambiguazione – Se stai cercando altri significati, vedi Allier (disambigua). Allierdipartimento LocalizzazioneStato Francia RegioneAlvernia-Rodano-Alpi AmministrazioneCapoluogoMoulins Presidente del Consiglio dipartimentaleClaude Riboulet[1] (UDI) dal 2017 Data di istituzione4 marzo 1790 TerritorioCoordinatedel capoluogo46°33′54.97″N 3°20′00″E46°33′54.97″N, 3°20′00″E (Allier) Superficie7 340 km² Abitanti341 613 (2015) Densit...












![{\displaystyle \left[{\begin{smallmatrix}0&1\\1&0\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331b1a58928ef146379335c0d30c79b61df0fb92)






![{\displaystyle \left[{\begin{smallmatrix}0&1\\0&-1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f35e354996e8c8fb3694418bb4333a8b41ea207)




















