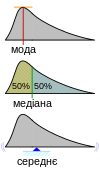
Середнє значення
|
Read other articles:

Bupati GowaPetahanaAdnan Purichta Ichsansejak 26 Februari 2021KediamanRumah Jabatan BupatiMasa jabatan5 tahunDibentuk1957Pejabat pertamaAndi Ijo Karaeng Lalolang Berikut ini adalah daftar bupati Gowa yang menjabat sejak pembentukannya pada tahun 1957. No Potret Bupati Mulai menjabat Akhir menjabat Partai Wakil Bupati Periode Ref. 1 Andi Ijo Karaeng Lalolang 1957 1960 N/A 1(1957) 2 Andi Tau 1960 1967 N/A 2(1960) 3 K.S. Mas'ud 1967 1976 N/A 3(1967) 4 H. M. Arief Siraju...

Questa voce sull'argomento calciatori lussemburghesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. François Weber Nazionalità Lussemburgo Calcio Ruolo Centrocampista Carriera Nazionale 1924 Lussemburgo1 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manual...

Collection of English words and their meanings, published by HarperCollins First edition The American Heritage Dictionary of the English Language (AHD) is a dictionary of American English published by HarperCollins. It is currently in its fifth edition (since 2011). Before HarperCollins acquired certain business lines from Houghton Mifflin Harcourt in 2022, the family of American Heritage dictionaries had long been published by Houghton Mifflin Harcourt and its predecessor Houghton Mifflin. T...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Season of television series Season of television series NCISSeason 2Season 2 U.S. DVD coverStarring Mark Harmon Sasha Alexander Michael Weatherly Pauley Perrette Sean Murray David McCallum No. of episodes23ReleaseOriginal networkCBSOriginal releaseSeptember 28, 2004 (2004-09-28) –May 24, 2005 (2005-05-24)Season chronology← PreviousSeason 1 Next →Season 3 List of episodes The second season of the police procedural drama NCIS was originally broadcast between Septe...

Questa voce sull'argomento calciatori slovacchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Ľubomír Tupta Nazionalità Slovacchia Altezza 180 cm Peso 72 kg Calcio Ruolo Attaccante Squadra Slovan Liberec CarrieraGiovanili 2009-2011 Slovan Sabinov2011-2014 Tatran Prešov2014-2015 Catania2015-2018 VeronaSquadre di club1 2015-2020 Verona19 (2)[1]2020→ &#...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2020) هذه المقالة عن عبد اللطيف الزين فنان تشكيلي مغربي. لمعانٍ أخرى، طالع عبد اللطيف الزين. عبد اللطيف الزين معلومات شخصية الميلاد 1940مراكش الوفاة 20 ديسمبر...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الحملة الصليبية العاشرة هي عبارة مجازية تربط بين الحرب على الإرهاب التي تقودها الولايات المتحدة الأمريك...

Nicole MainesLahirWyatt Benjamin Maines07 Oktober 1997 (umur 26)Gloversville, New York, Amerika SerikatPekerjaanAktris, aktivis [1]Tahun aktif2015, 2018–sekarangDikenal atasSusan Doe dalam kasus Mahkamah Agung Maine Doe v. Regional School Unit 26SupergirlOrang tuaWayne dan Kelly MainesKerabatJonas Zebediah Maines (kembar identikal) Nicole Amber Maines (lahir 7 Oktober 1997) adalah seorang aktris dan aktivis hak transgender Amerika Serikat.[2][3][4]...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Teletsentr – news · newspapers · books · scholar · JSTOR (December 2015) (Learn how and when to remove this message) Moscow Monorail station TeletsentrТелецентрMoscow Monorail stationGeneral informationLocationOstankinsky DistrictNorth-Eastern Administrative OkrugMoscow...

You can help expand this article with text translated from the corresponding article in French. (January 2010) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipe...

塔里木河流域源頭喀喇昆仑山脉特力木坎力峰 - 坐標35°32′53″N 77°28′58″E / 35.547983°N 77.482907°E / 35.547983; 77.482907 - 海拔7464 第二源头北里莫冰川 - 坐標35°29′17″N 77°26′52″E / 35.488°N 77.4479°E / 35.488; 77.4479 第三源头喀喇昆仑山口 - 坐標35°30′48″N 77°49′22″E / 35.51346°N 77.8227°E / 35.51346; 77....

Extirpation of Irish wolves Legend of Priest and Were-Wolves from Gerald de Barri's Topographia Hibernica. Preserved wolf in the National Museum of Ireland – Natural History The Grey wolf (Canis lupus) was an integral part of the Irish countryside and culture, but are now extinct. The last wild wolf in Ireland is said to have been killed in 1786, 300 years after they were believed to have been wiped out in England and 100 years after their disappearance from Scotland.[1][2] ...

الفِلِبِّين (بالفلبينو: Pilipinas [pɪlɪˈpinɐs])، رسمياً جمهورية الفلبين، هي جمهورية دستورية تقع في جنوب شرق آسيا غرب المحيط الهادي. عبارة عن أرخبيل مكون من 7107 جزيرة، تحده تايوان إلى الشمال عبر مضيق لوزون، وفيتنام إلى الغرب عبر بحر الصين الجنوبي. بحر سولو في الجنوب الغربي يفصلها عن ...

Pemilihan umum Bupati Tulang Bawang 20242017202927 November 2024Kandidat Peta persebaran suara Bupati & Wakil Bupati petahanaWinarti & Hendriwansyah Partai Demokrasi Indonesia Perjuangan Bupati & Wakil Bupati terpilih belum diketahui Pemilihan umum Bupati Tulang Bawang 2024 dilaksanakan pada 27 November 2024 untuk memilih Bupati Tulang Bawang periode 2024-2029.[1] Pemilihan Bupati (Pilbup) Tulang Bawang tahun tersebut akan diselenggarakan setelah Pemilihan umum Presiden I...

orange ジャンル SF、青春、恋愛漫画、学園漫画少女漫画、青年漫画 漫画 作者 高野苺 出版社 集英社 / 双葉社 掲載誌 別冊マーガレット月刊アクション レーベル マーガレットコミックスACTION COMICS 発表号 別冊マーガレット:2012年4月号[1] - 12月号月刊アクション:2014年2月号[2] - 2015年10月号[3](本編)2016年4月号[4](番外編) 発表期間 2012年3月13日 -...

Disused railway line in Yorkshire, England Harrogate–Church Fenton lineProspect TunnelOverviewStatusClosed from Crimple junction to Church Fenton junctionLocaleNorth YorkshireTerminiHarrogateChurch Fenton North JunctionStations8ServiceTypeHeavy railOperator(s)York and North Midland Railway to 1854North Eastern Railway 1854–1923London and North Eastern Railway 1923–1948British Railways (N.E region) 1948 to closureDepot(s)Harrogate Low (Brunswick, closed 1862)[1]HistoryOpened10 Au...

معاهدة سيفرمعاهدة السلام بين الدولة العثمانية وبين الحلفاء وشركائهم.تقسيم تركيا العثمانية وفقا لمعاهدة سيفر المجهضةمعلومات عامةالنوع معاهدة سلام — معاهدة متعددة الأطراف نسبة التسمية سيفر التوقيع 10 أغسطس 1920الموقعون دول المركز الدولة العثمانية دول الحلفاء فرنسا إ...










![{\displaystyle (4\times 36\times 45\times 50\times 75)^{^{1}/_{5}}={\sqrt[{5}]{24\;300\;000}}=30.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c4425218d27488f26ff3f661a0e6df4ad676e59)