Канонічна кореляція
|
Read other articles:

Patung Kebebasan di Bukit Gellért Patung Kebebasan (Hongaria: Szabadság-szoborcode: hu is deprecated [ˈsɒbɒtt͡ʃaːɡ ˈsobor]) adalah sebuah tugu peringatan yang terletak di Bukit Gellért di Budapest, ibu kota Hungaria. Tugu peringatan ini didirikan pada tahun 1947 dengan maksud untuk mengenang peristiwa ketika Tentara Merah membebaskan Hungaria dari cengkeraman Nazi dan menjatuhkan Pemerintahan Persatuan Nasional menjelang akhir Perang Dunia II. Maka dari itu, di tugu ini pada awalny...

Daniel Chipman Daniel Chipman (22 Oktober 1765 – 23 April 1850) merupakan seorang politikus berkebangsaan Amerika. Ia bekerja sebagai Dewan Perwakilan Rakyat Amerika Serikat dari Vermont. Karya yang diterbitkan “Life of Nathaniel Chipman” “Memoirs of Thomas Chittenden, First Governor of Vermont” Essay of Law of Contracts Memoirs of Col. Seth Warner Referensi Bacaan selanjutnya Speech of Hon. Daniel Chipman, published by E.R. Jewett, 1837. Pranala luar Biographical Direc...

Mark Stevensdalam The Dark Corner (1946)LahirRichard William Stevens(1916-12-13)13 Desember 1916Cleveland, Ohio, Amerika SerikatMeninggal15 September 1994(1994-09-15) (umur 77)Majores, SpanyolNama lainStephen RichardsTahun aktif1943–1987Suami/istriAnnelle Hayes (m. 1945–1962) (bercerai)Anak2 Mark Stevens (nama lahir: Richard William Stevens, 13 Desember 1916 – 15 September 1994) adalah seorang pemeran Ameri...

English peer Thomas Thynne, 2nd Viscount Weymouth Arms of Thomas Thynne, 2nd Viscount Weymouth: Barry of ten or and sable (Botteville); 2nd and 3rd: Argent, a lion rampant tail nowed and erect gules (Thynne) Thomas Thynne, 2nd Viscount Weymouth (21 May 1710 – 1751) of Longleat House in Wiltshire was an English peer, descended from Sir John Thynne (c.1515-1580) builder of Longleat. Origins He was born on 21 May 1710, the son of Thomas Thynne (d.1710) by his wife Lady Mary Villiers.[1]...

استخدم المؤتمر الوطنيعلم الجمهورية الليبية وأصبح في نهاية المطاف العلم الرسمي لليبيا بعد الإطاحة بمعمر القذافي.[1] كان المؤتمر الوطني للمعارضة الليبية (NCLO) عبارة عن منظمة ليبية معارضة في السنوات الأخيرة من نظام القذافي. وكان هدفها المعلن هو وضع «نهاية للاستبداد وإقامة...

العلاقات العمانية السويسرية سلطنة عمان سويسرا سلطنة عمان سويسرا تعديل مصدري - تعديل العلاقات العمانية السويسرية هي العلاقات الثنائية التي تجمع بين سلطنة عمان وسويسرا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه...

Romanian football club, formerly FC Steaua București This article is about the club officially named FCSB. For the other team claiming to be the legal successor of the original Steaua București and affiliated with the multi-sport club and the army, see CSA Steaua București (football). For other uses, see Steaua București (disambiguation). Football clubFCSBFull nameSC Fotbal Club FCSB SANickname(s)Roș-albaștrii (The Red and Blues)Short nameFCSBFounded7 June 1947; 76 years ag...

Jalanan di Eminence, Missouri Eminence adalah sebuah kota di Shannon County, Missouri, Amerika Serikat. Populasi adalah 515 pada sensus 2020 .[1] Ini adalah ibu kota Kabupaten Shannon County.[2] Sejarah Sebuah kantor pos bernama Eminence telah beroperasi sejak tahun 1844.[3] Menurut satu akun, Eminence dinamai demikian karena ketinggiannya yang tinggi,[4] namun, interpretasi ini diperdebatkan.[5] Geografi Eminence terletak di tengah Ozark National Sceni...

Recopa Sudamericana 1998 Competizione Recopa Sudamericana Sport Calcio Edizione 10ª Organizzatore CONMEBOL Partecipanti 2 Risultati Vincitore Cruzeiro(1º titolo) Secondo River Plate Cronologia della competizione 1997 2003 Manuale La Recopa Sudamericana 1998 è stata la decima edizione della Recopa Sudamericana; in questa occasione a contendersi la coppa furono il vincitore della Coppa Libertadores 1997 e il vincitore della Supercoppa Sudamericana 1997. Indice 1 Tabellino 1.1 An...
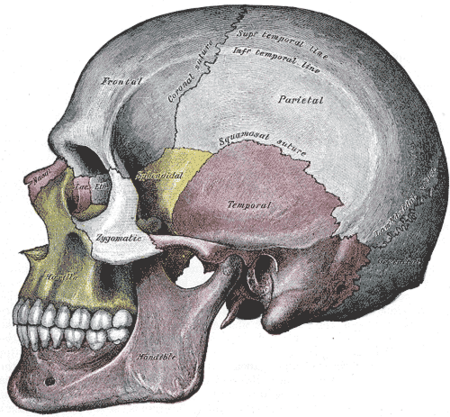
Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Cranio umano, vista frontaleCranio umano, vista laterale Il cranio è la struttura scheletrica, cartilaginea e/o ossea, presente nella testa dei Vertebrati. Assieme alla colonna vertebrale e alle coste forma lo scheletro assile, che viene distinto da quello appendicolare (ossa degli arti, cintura scapolare e c...

US Supreme Court justice from 1877 to 1911 This article is about the pre–World War I United States Supreme Court justice. For his grandson, the mid-20th century holder of the same position, see John Marshall Harlan II. The Great Dissenter redirects here. For the Australian judge with the same nickname, see Michael Kirby (judge). John Marshall HarlanAssociate Justice of the Supreme Court of the United StatesIn officeDecember 10, 1877 – October 14, 1911Nominated byRutherford B. Hay...

Rare genetic condition Medical conditionRubinstein–Taybi syndromeOther namesBroad thumb-hallux syndrome or Rubinstein syndrome[1]Child with Rubinstein–Taybi syndromeSpecialtyMedical genetics Causesmutation or deletion in the CREBBP gene, located on chromosome 16, and/or the EP300 gene, located on chromosome 22. Rubinstein–Taybi syndrome (RTS) is a rare genetic condition characterized by short stature, moderate to severe learning difficulties, distinctive facial features, an...

Финляндская православная церковь(Финляндская архиепископия)фин. Suomen ortodoksinen kirkkoшвед. Ortodoxa kyrkan i Finland Успенский кафедральный собор Общие сведения Основатели Тихон Основание 1921 Конфессия православие Церковь-мать Московский патриархат Автономия 11 февраля 1921 года Признан�...

ميثولوجيا كلتيةمعلومات عامةصنف فرعي من علم الأساطير جزء من وثنية كلتية المجموعة العرقية قلط الثقافة Celtic people (en) قلطProto-Celts (en) أصيل في Proto-Celts (en) قلط لديه جزء أو أجزاء أساطير أيرلنديةأساطير اسكتلنديةأساطير ويلزية تعديل - تعديل مصدري - تعديل ويكي بيانات سلسلة من المقالات حولال�...

French physicist Hubert CurienMinister of Research and TechnologyIn office1984–1986PresidentFrançois MitterrandPrime MinisterLaurent FabiusPreceded byNicole CathalaSucceeded byRobert Chapuis Personal detailsBorn(1924-10-30)30 October 1924Cornimont, FranceDied6 February 2005(2005-02-06) (aged 80)Loury, FranceSpousePerrine DumézilChildren3EducationLycée Saint-LouisAlma materÉcole normale supérieureOccupationPhysicistAwardsHonda Prize (1998)Allan D. Emil Memorial Award (1993) Solvay ...

بيت طيما الإحداثيات 31°37′24″N 34°38′21″E / 31.62333333°N 34.63916667°E / 31.62333333; 34.63916667 تقسيم إداري البلد فلسطين الانتدابية التقسيم الأعلى قضاء غزة تعديل مصدري - تعديل بيت طيما هي قرية فلسطينية في قضاء غزة، وتقع 21 كيلومترا (13 ميل) إلى الشمال الشرقي من غزة وحوال...

Mythical character For other uses, see Pelops (Sparta) and Pelops (mythology). PelopsKing of PisaAbodePisaPersonal informationParentsTantalus and DioneSiblingsNiobeBroteasConsortHippodamiaAxiocheOffspringAtreus, Thyestes, Nicippe, Pittheus, Chrysippus, and others Part of a series onGreek mythology Deities Primordial Titans Olympians Nymphs Water Chthonic Heroes and heroism Heracles Labours Achilles Hector Diomedes Trojan War Odysseus Odyssey Jason Argonauts Golden Fleece Perseus Medusa Gorgon...

USA-related events during the year of 1943 ← 1942 1941 1940 1943 in the United States → 1944 1945 1946 Decades: 1920s 1930s 1940s 1950s 1960s See also: History of the United States (1918–1945) Timeline of United States history (1930–1949) List of years in the United States 1943 in the United States1943 in U.S. states and territories States Alabama Arizona Arkansas California Colorado Connecticut Delaware Florida Georgia Idaho Illinois Indiana Iowa Kansas Kentucky Louisiana Mai...

Field howitzer D-1 howitzer TypeField howitzerPlace of originSoviet UnionService historyIn service1943–presentUsed byCountries of the former Warsaw Pact and former Soviet UnionWarsWorld War IIArab-Israeli WarVietnam War2022 Russian invasion of UkraineProduction historyDesignerF. F. PetrovDesigned1943ManufacturerNo. 9 PlantProduced1943–1949No. built2,827VariantsD-15, M1943/85SpecificationsMass3,600 kg (7,937 lbs)Length6.7 m (22 ft)Barrel lengthBore:...

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to the following WikiProjects:Merseyside Mid‑importance North West England portalThis template is within the scope of WikiProject Merseyside, a collaborative effort to improve Wikipedia's coverage of Merseyside-related articles. In so doing it works and collaborates with its mother project WikiProject UK Geography. If you would like to participate, please visit the project page, where you can j...























































![{\displaystyle \Sigma _{XX}=\operatorname {Cov} (X,X)=\operatorname {E} [XX']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a701c9582fe6eae0cceeb721deb5cb64f19b8b)
![{\displaystyle \Sigma _{YY}=\operatorname {Cov} (Y,Y)=\operatorname {E} [YY']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/038b2015e4aaac448085974158fb16ccb57b58c8)




