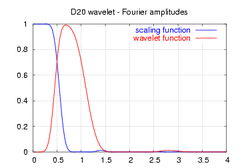
Вейвлет
|
Read other articles:

Cerita Spesial DoraemonGenreKomedi MangaPengarangFujiko F. FujioPenerbitElex Media KomputindoVolume18 Portal anime dan manga Cerita Spesial Doraemon adalah salah satu dari edisi manga Doraemon karya Fujiko F. Fujio yang diterbitkan di Indonesia oleh Elex Media Komputindo. Edisi ini berisi penggolongan cerita berdasarkan suatu tema, contohnya tema purbakala dimuat dalam edisi 1: Dinosaurus. Sebenarnya komik ini hanya penjilidan ulang dari kisah Doraemon versi reguler edisi 1-45, tak ...

Untuk tempat lain yang bernama sama, lihat Chełmek. Chełmek Lambang kebesaranChełmekKoordinat: 50°7′N 19°15′E / 50.117°N 19.250°E / 50.117; 19.250Negara PolandiaVoivodeshipPolandia KecilPowiatOświęcimGminaChełmekPemerintahan • Wali kotaAndrzej SaternusLuas • Total8,31 km2 (321 sq mi)Populasi (2006) • Total9.065 • Kepadatan11/km2 (28/sq mi)Zona waktuUTC+1 (CET) • Musi...

Leicester City Football Club adalah sebuah klub sepak bola yang berasal dari Leicester, Inggris. Tim ini bermain di kasta kedua sepak bola inggris, Kejuaraan EFL dan bermarkas di King Power Stadium.Leicester CityNama lengkapLeicester City Football ClubJulukanThe Foxes (rubah),The Filberts,The Blues (biru)Berdiri1884; 139 tahun lalu (1884)(sebagai Leicester Fosse FC)StadionKing Power(Kapasitas: 32.312[1])PemilikKing Power International GroupKetua Aiyawatt SrivaddhanaprabhaManajer ...

Final Piala Raja Spanyol 1921TurnamenPiala Raja Spanyol 1921 Athletic Bilbao Atlético Madrid 4 1 Tanggal8 Mei 1921StadionStadion San Mamés, BilbaoWasitJosé Angel Berraondo (Spanyol)Penonton15.000← 1920 1922 → Final Piala Raja Spanyol 1921 adalah pertandingan final ke-19 dari turnamen sepak bola Piala Raja Spanyol untuk menentukan juara musim 1921. Pertandingan ini diikuti oleh Athletic Bilbao dan Atlético Madrid dan diselenggarakan pada 8 Mei 1921 di Stadion San Mamés, Bilbao...

Women's lacrosse team This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Baltimore Brave – news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this template message) BraveFounded2018LeagueWomen's Professional Lacrosse LeagueHead coachSonia LaMonicaGeneral managerJessy Morga...

Terrorism involving biological agents Part of a series onTerrorism Definitions History Incidents By ideology Anarchist Communist Left-wing/Far-left Narcotics-driven Nationalist Right-wing/Far-right Religious Buddhist Christian (Mormon) Hindu Islamic (Salafi-Wahhabi) Jewish Sikh Special-interest / Single-issue Suffragette Anti-abortion Green/Ecological Misogynist Related topics Violent extremism Ethnic violence Militia movement Resistance movement Structure Financing Fronting Radicali...

Transitional dialect RoyascRoiascNative toItaly, FranceNative speakers(undated figure of approximately 3,000[citation needed])Language familyIndo-European RomanceWesternGallo-RomanceGallo-ItalicLigurianRoyascLanguage codesISO 639-3–GlottologNoneLinguaspherenone Royasc is a dialect bridging the gap between the Ligurian language and the Occitan language. It is spoken in Italy and France. Area of use Area of Royasc in France (blue) and Italy (orange and green) The Royasc dialect i...

Henri Antoine Jardon Le général Jardon, commandant de l'avant-garde de l'armée du Nord, gravure d'époque. Surnom « Le général voltigeur » Naissance 3 février 1768Verviers, principauté de Liège Décès 25 mars 1809 (à 41 ans)Guimarães, PortugalMort au combat Origine Belge Allégeance États belgiques unis (1789-1790) Royaume de France (1792) République française (1792-1804) Empire français (1804-1809) Arme Infanterie Grade Général de brigade Années ...

Kup kralja Aleksandra 1924 Competizione Kup kralja Aleksandra Sport Calcio Edizione 1ª Organizzatore JNS Date dal 24 agosto 1924al 4 ottobre 1924 Luogo Regno dei Serbi, Croati e Sloveni Partecipanti 7 Formula Eliminazione diretta Risultati Vincitore Zagabria XI(1º titolo) Secondo Spalato XI Semi-finalisti Lubiana XISubotica XI Cronologia della competizione 1925 Manuale La Kup kralja Aleksandra 1924., in serbo Куп краља Александра 1924. (in italiano Coppa del re Al...

Australian politician Eric DeckerMember of the Queensland Legislative Assemblyfor SandgateIn office29 March 1941 – 7 March 1953Preceded byRoland HislopSucceeded byHerbert Robinson Personal detailsBornEric Paul Decker(1896-11-22)22 November 1896Roma, Queensland, AustraliaDied7 July 1970(1970-07-07) (aged 73)Sandgate, Queensland, AustraliaPolitical partyLiberal PartyOther politicalaffiliationsQueensland People's Party, Country PartySpouseEden Templeton Kemp (m.1926 d.1990) Eric ...

Cricket role Jason Gillespie holds the record for the highest Test score from a nightwatchman, scoring 201* against Bangladesh at the Chittagong Divisional Stadium during the second test of Australia's 2005-06 tour of Bangladesh In the sport of cricket, a nightwatchman is a lower-order batter who comes in to bat higher up the order than usual near the end of the day's play.[1] The nightwatchman's job is to maintain most of the strike until the close of play. The name comes due to the ...

Katedral SevillaKatedral Metropolitan Santa Maria dari Takhtabahasa Spanyol: Catedral de Santa María de la SedeKatedral SevillaLokasiSevilla, AndalusiaNegaraSpanyolDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifArsitekAlonso Martínez, Pedro Dancart, Carles Galtés de Ruan, Alonso RodríguezPeletakan batu pertama1401Selesai1528AdministrasiKeuskupan AgungKeuskupan Agung Sevilla Katedral Santa Maria dari Takhta (bahasa Spanyol: Catedral de Santa María de la...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Overview of territorial changes of the Baltic states after 1940 This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Territorial changes of the Baltic states – news · newspapers&...

American record label For other uses, see Dot (disambiguation). Dot RecordsParent companyIndependent (1950–57)Paramount Pictures (1957–72)Gulf+Western (1966–74)Famous Music Group (1972–74)ABC Records (1974–78)MCA Records (1985–86)Universal Music Group (2014–17)Founded1950 (1950) (original)2014 (revival)FounderRandy WoodGene NoblesDefunct1978 (1978) (original)2017 (2017) (revival)StatusDefunctDistributor(s)Self-distributed (1950–68)Famous Music Group (1968–74)A...

Public university in Colombia This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Technological University of Chocó – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) Diego Luis Cordoba Technological University of ChocoUniversidad Tecnológica del Chocó Diego Luis CórdobaForme...

موسم التناسل أو موسم التكاثر أو موسم التفريخ، هو تلك الفترة المُفضَّلة من السنة عند الكثير من الحيوانات من ثدييات وطيور وغيرها لتتكاثر وتُنجب صغارها، وهي في العادة الفترة التي يَكثرُ فيها الطعام والماء، وتكون الظروف المناخيَّة مؤاتية. تكيَّفت الحيوانات التي تُنجب خلال م...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2023) وزارة السلام (إثيوبيا) تفاصيل الوكالة الحكومية البلد إثيوبيا تأسست أكتوبر 2018 المركز أديس أبابا الإدارة موقع الويب الموقع الرسمي تعديل مصدري - �...

American filmmaker (1925–2006) For other people named Robert Altman, see Robert Altman (disambiguation). Robert AltmanAltman in 1983BornRobert Bernard Altman(1925-02-20)February 20, 1925Kansas City, Missouri, U.S.DiedNovember 20, 2006(2006-11-20) (aged 81)Los Angeles, California, U.S.OccupationFilmmakerYears active1947–2006Known forM*A*S*H (1970) McCabe & Mrs. Miller (1971) The Long Goodbye (1973) Nashville (1975) 3 Women (1977) Popeye (1980) The Player (1992) Short Cut...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: SMA Santo Thomas – berita · surat kabar · buku · cendekiawan · JSTOR SMA Santo Thomas Didirikan sejak 28 Oktober 1946, SMA Santo Thomas tetap konsisiten memberikan pelayanan pendidikan untuk jenjang pend...


![{\displaystyle f(x)\in C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be15390c7b41cf30547ae8000462aca01dd039c4)







![{\displaystyle I_{n}=[k2^{-j},(k+1)2^{-j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81adc0a3a74c5d793c611e8e151df5b11236cb92)


![{\displaystyle L_{2}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7e14db4046a553ac5100be1fbc406ca81cb5cc0)