Спільний розподіл
|
Read other articles:

Lukman SardiLukman ketika berpidato di Festival Film Indonesia pada tahun 2019Lahir14 Juli 1971 (umur 52)Jakarta, IndonesiaPekerjaanAktorprodusersutradaraTahun aktif 1977—1980 2002—sekarang Suami/istriPricillia Pullunggono (m. 2009)Anak3Orang tuaIdris Sardi (bapak)Keluarga Sardi (kakek) Hadidjah (nenek) Santi Sardi (kakak) Ajeng Triani Sardi (adik) Meirayni Fauziah (sepupu) Shelomita (adik tiri) Reuben Elishama (adik tiri) Lukman Sardi (la...

Public university in Las Cruces, New Mexico, US NMSU redirects here. For the university in Missouri, see Northwest Missouri State University. New Mexico State redirects here. For the U.S. state, see New Mexico. New Mexico State UniversityFormer namesLas Cruces College (1888–1889)New Mexico College of Agriculture and Mechanic Arts (1889–1960)TypePublic land-grant research universityEstablishedSeptember 17, 1888; 135 years ago (1888-09-17)AccreditationHLCAcademic affiliati...

У этого термина существуют и другие значения, см. ГИС. Геоинформационная система (географическая информационная система, ГИС) — система сбора, хранения, анализа и графической визуализации пространственных[1] (географических) данных и связанной с ними информации о ...

À Genève, devant l'Organisation mondiale de la santé, la vaccination est érigée en statue, œuvre du sculpteur Martin William dévoilée le 17 mai 2010, date de la commémoration du 30e anniversaire de l'éradication de la variole[1] : un agent de santé utilise une aiguille bifurquée à la place du vaccinostyle, afin de vacciner toute une famille contre la variole. Administration d'un vaccin. La vaccination est l'administration d'un agent antigénique, le vaccin, dans le but de st...

Pemandangan kota di malam hari Lambang kota Untuk pengertian lain, lihat Deva. Deva (bahasa Jerman: Diemrich, bahasa Hungaria: Déva) ialah sebuah kota di Transilvania, di paruh tengah Sungai Mureş di Rumania. Deva merupakan ibu kota Provinsi Hunedoara dan berpenduduk 65.000 jiwa. Sejarah Pada masa kuno terdapat benteng bernama Decidava. Bukti tertulis atas kota ini berasal pada tahun 1269. Di bawah Voivod Johan Hunyadi Deva menjadi pusat militer dan administratif yang penting. Hancur sebagi...

American punk band MxPxMxPx performing in 2008, showing Tom Wisniewski and Mike HerreraBackground informationAlso known asMagnified Plaid[1]OriginBremerton, Washington, U.S.[1]Genres Punk rock pop-punk skate punk Christian punk (early) Years active1992–present[1]Labels Tooth & Nail A&M Fat Wreck Chords SideOneDummy Rock City Recording Company SpinoffsArthurMembers Mike Herrera Yuri Ruley Tom Wisniewski Chris Adkins Past members Andy Husted Websitemxpx.com MxP...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Kuil Buddharama di Torsby, Munisipalitas Värmdö Buddhisme adalah agama minoritas di Swedia. Sebagian besar pemeluk agama Buddha di Swedia adalah orang-orang berdarah Asia (kebanyakan orang Thai, Han, dan Vietnam). Pada 2015, Dewan Kerjasama Buddhis S...

For other uses, see Moriah (disambiguation). Mountain in the state of New Hampshire Mount MoriahMt. Moriah (center) from GorhamHighest pointElevation4,049 ft (1,234 m)[1]Prominence922 ft (281 m)[1]Parent peakNorth Carter Mountain[1]ListingAMC New England Hundred Highest[2]Coordinates44°20′25″N 71°07′53″W / 44.3403408°N 71.1314634°W / 44.3403408; -71.1314634[3]GeographyMount Moriah Locatio...

الاسفنجة المقدسة هي إحدى الات صلب يسوع.[1][2][3] غمست الاسفنجة في الخل (أو نبيذ حامض حسب بعض الترجمات) وقدمت للمسيح ليشرب منها خلال الصلب حسب اناجيل متى ومرقس ويوحنا. في بداية القرن السابع وجدت الاسفنجة في فلسطين وقدست مراجع ^ Chapelle Sixtine, الفاتيكان. [وصلة مكسورة] �...

Lukisan Kristus dan Buddha (1880) karya Paul Ranson. Dalam kajian perbandingan antara agama Buddha dan Kristen, sejumlah kesamaan dianggap terkandung dalam dua agama tersebut,[1] bermula sejak misionaris Kristen tiba di Dunia Timur pada abad ke-13, diikuti dengan kehadiran agama Buddha di Eropa Barat pada abad ke-18 dan ke-19.[2] Selama abad ke-20, perbedaan antara dua agama tersebut juga mendapat sorotan.[3] Meskipun tampaknya ada kemiripan, agama Buddha dan Kristen m...
XXX — символ порнографії Порногра́фія (грец. πόρνη (порні) — «повія» і грец. γραφή (графі) — писання) — натуралістичне зображення сексуальної практики в живописі, літературі, кіно, фотографії тощо, або словесне описання статевого акту, що мають за мету сексуа�...

Pour les articles homonymes, voir Legia Varsovie. Legia Varsovie Généralités Nom complet Legia Warszawa SA Surnoms Wojskowi (les militaires), Legioniści (les légionnaires)[1] Fondation Mars 1916[Note 1] Statut professionnel Depuis 1922 Couleurs Blanc, vert, noir et rouge Stade Stade du maréchal Józef Piłsudski (31 103 places) Siège 3 rue Łazienkowska,00-449 Varsovie Championnat actuel Ekstraklasa (1re division) Président Dariusz Mioduski Entraîneur Gonçalo Feio Joueur ...

Azerbaijan geopolitical map with rail and road network The transport in Azerbaijan involves air traffic, waterways and railroads. All transportation services in Azerbaijan except for oil and gas pipelines are regulated by the Ministry of Transportation of Azerbaijan Republic.[1] For Soviet transportation, see Transport in the Soviet Union. Railways Azerbaijan Railways map (current) Main article: Azerbaijan Railways There are 2,932 km (1,822 mi) of rail tracks out of which o...

Capture de mouvement Un danseur portant une combinaison avec des marqueurs passifs réfléchissants, lors d'une capture optique de mouvement. Données clés Acronyme mocap Transcription Motion Capture Domaine d'application Prise de vues cinématographique Date de création années 1990 Données clés Invention parente chronophotographie La capture de mouvement[1],[2] (motion capture en anglais, parfois abrégé en mocap) est une technique permettant d'enregistrer les positions et rotations d...

Pour les articles homonymes, voir Réhabilitation. Cet article est une ébauche concernant l’architecture ou l’urbanisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Dans le domaine de l'urbanisme et de l'architecture, la réhabilitation désigne au sens large le fait de réaménager un local, un bâtiment ou un lieu (quartier, friche, es...

Pour des articles plus généraux, voir Chronologie des États-Unis et 1928. Éphémérides Parade du Ku Klux Klan à Washington, D.C.Chronologie des États-Unis 1925 1926 1927 1928 1929 1930 1931Décennies aux États-Unis :1890 1900 1910 1920 1930 1940 1950 Chronologie dans le monde 1925 1926 1927 1928 1929 1930 1931Décennies :1890 1900 1910 1920 1930 1940 1950Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-...

British Christian theologian and scholar (1635–1699) For his son, the English physician and clergyman, see Edward Stillingfleet (physician). Portrait of Bishop Stillingfleet by Mary Beale, circa 1690 Christianity portal Edward Stillingfleet (17 April 1635 – 27 March 1699) was a British Christian theologian and scholar. Considered an outstanding preacher as well as a strong polemical writer defending Anglicanism, Stillingfleet was known as the beauty of holiness for his good looks in the p...
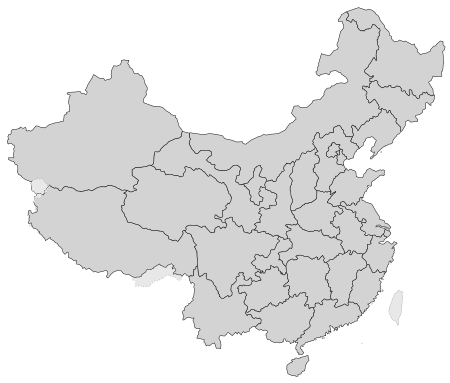
Administrative divisionsof China Province-level (1st)Municipalities Provinces Autonomous regions Special administrative regions Sub-provincial levelSub-provincial cities Sub-provincial autonomous prefectures Sub-provincial city districts Prefecture-level (2nd)Prefectural cities Autonomous prefectures Leagues (Aimag) (abolishing) Prefectures (abolishing) Sub-prefectural-levelSub-prefectural cities Provincial-controlled cities Provincial-controlled counties Provincial-controlled districts Coun...

The Nieuwerkerk Windmill in 2015 The Nieuwerkerk Windmill is a grain mill in Nieuwerkerk, Netherlands. History The tower mill was built in 1844 to replace a wooden octagonal mill that had burned down, probably after lightning.[1] In 1970 the mill was sold to the municipality of Duiveland that has since been merged with other municipalities into Schouwen-Duiveland. The mill was preserved after the North Sea flood of 1953 but has had problems for a long time due to the saltwater that ha...

Ability to experience feelings and sensations Not to be confused with Sapience. Sentient redirects here. For other uses, see Sentient (disambiguation). Determining which animals can experience sensations is challenging, but scientists generally agree that vertebrates, as well as many invertebrate species, are likely sentient.[1][2] Sentience is the ability to experience feelings and sensations.[3] It may not necessarily imply higher cognitive functions such as awarenes...
































