Коефіцієнт кореляції рангу Кендала
|
Read other articles:

Cosiddetta Flora, affresco romano da Villa Arianna a Stabia, I secolo. Flora è la dea romana e italica della fioritura dei cereali[1] e delle altre piante utili all'alimentazione, compresi vigneti e alberi da frutto.[2] Col tempo venne intesa come dea della primavera. Indice 1 Generalità 2 Flora nella letteratura e nell'arte 2.1 Flora secondo Lattanzio 2.2 Flora al di fuori di Roma 2.3 Flora nelle epoche successive 3 Flora nella musica 4 Galleria d'immagini 5 Note 6 Voci cor...

Building in Washington, D.C. which served as the US Capitol from 1815–19 Old Brick CapitolPart of American Civil War prison campsThe former Old Brick Capitol building serving as a prison during the American Civil War, 1861-1865TypeUnited States Capitol (1815–1819)Union Prison Camp (1861–1865)Site informationOwnerU.S. federal governmentControlled byUnion ArmyOpen tothe publicNoSite historyBuilt1815In use1815–18191861–1867MaterialsbrickDemolished1929Battles/warsAme...

Font used in the US for highway signs Highway GothicCategorySans-serifDesigner(s)Ted ForbesFoundryN/ADate released1948Sample Highway Gothic (formally known as the FHWA Series fonts or the Standard Alphabets for Highway Signs) is a sans-serif typeface developed by the United States Federal Highway Administration (FHWA) and used for road signage in the Americas, including the U.S., Canada, Latin America and some Caribbean countries, as well as in Asian countries influenced by American signage p...

Caramelo e' Chocolate Serie de televisiónGénero TelenovelaDirigido por Nicolas Di BlasiTema principal Caramelo y ChocolateAmbientación 2015País de origen Guatemala GuatemalaN.º de episodios 120 capítulosLanzamientoMedio de difusión TelevisieteHorario Lunes a viernes a las 9:00 p. m..Audiencia 3.35 puntos de índice de audiencia4,4 de shareFecha de lanzamiento 10 de junio de 2015Cronología de producciónCaramelo e' ChocolateHospital y Emergencía[editar datos en Wikidata...

LevittownLevittown station viewed from the outbound platform in 2019General informationLocation8301 Bristol PikeTullytown, PennsylvaniaCoordinates40°08′25″N 74°49′02″W / 40.1402°N 74.8172°W / 40.1402; -74.8172Owned bySoutheastern Pennsylvania Transportation AuthorityLine(s)Amtrak Northeast CorridorPlatforms2 side platformsTracks4Connections SEPTA Suburban Bus: 127[1]ConstructionParking452 spaces[2]Bicycle facilities8 rack spaces[2]Ac...

لمعانٍ أخرى، طالع كلي (توضيح). الكلي (جمعها كليات) في الفلسفة هو أحد أصناف الكيانات العقلية المجردة المستقلة حسب ما تعرفها الفلسفة الواقعية، حيث يفترض أن هذه الكليات هي التي تؤسس وتشرح العلاقة بين الماهيات النوعية والتشابه بين الأفراد.[1][2] يمكننا أن نقول عن ا...

American theatre director This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Virlana Tkacz – news · newspapers · books · scholar · JSTOR (March 2018) (Learn how and when to remove this message)Virl...

Public high school in Greenwood Village, Colorado, United StatesCherry Creek High SchoolAddress9300 East Union AvenueGreenwood Village, Colorado 80111United StatesCoordinates39°37′50″N 104°52′48″W / 39.63056°N 104.88000°W / 39.63056; -104.88000InformationSchool typePublic high schoolEstablishedSeptember 6, 1955 (68 years ago) (1955-09-06)[1]School districtCherry Creek 5CEEB code060515NCES School ID080291000186[2]PrincipalRyan S...

USO beralih ke halaman ini. Untuk kegunaan lain, lihat USO (disambiguasi). The United Service OrganizationsTanggal pendirian4 February 1941[1]TipeServicesFokusUSO mempererat para anggota layanan militer Amerika dengan menjaga hubungan mereka dengan keluarga, tempat tinggal dan negara, sepanjang penugasan mereka di suatu negara.LokasiArlington, VirginiaWilayah layanan 160+ pusat di seluruh duniaTokoh pentingJ.D Crouch IIPresiden dan CEOPendapatan Amal (sebuah nirlaba 501(c)(3))Jumlah s...

Не путать с конкурсом «Мисс Вселенная Япония», который проходит с 1998 года Мисс Япония (яп. ミス日本コンテスト Мису Ниппон контэсуто) — ежегодный национальный конкурс красоты в Японии, проходящий с 1950 года. Победительницы 1950 — Фудзико Ямамото 1968 — Норико Судзуки 1...

New York City Subway station in the Bronx For the former terminal station slightly to the northwest, see 180th Street–Bronx Park station. New York City Subway station in The Bronx, New York East 180 Street New York City Subway station (rapid transit)Northbound view of the station platforms before renovation, with the East 180th Street Yard off to the left.Station statisticsAddressEast 180th Street & Morris Park AvenueBronx, New YorkBoroughThe BronxLocaleVan Nest and We...

Peter Monteverdi Peter Monteverdi (Binningen, 7 giugno 1934 – Binningen, 4 luglio 1998) è stato un imprenditore e pilota automobilistico svizzero, fondatore dell'omonima casa automobilistica. Indice 1 Biografia 2 Note 3 Altri progetti 4 Collegamenti esterni Biografia Figlio di un meccanico, Peter Monteverdi nel 1956 subentrò al padre, deceduto, nella gestione della sua officina, alla quale affiancò la progettazione e la costruzione di automobili da corsa (inizialmente go-kart per la Form...

German opera singer Plaque in tribute to Johann Theodor Mosewius in Wrocław Johann Theodor Mosewius also Johann Theodor Mosevius (birth name Moses) (25 September 1788 – 15. September 1858) was a German operatic bass, choirmaster and music director of the University of Wroclaw.[1] Life Mosewius was born in Königsberg. After studying law, he trained as an opera singer (bass) and worked as such at the local theatre, at the time of the management of August von Kotzebue (1814-1816), th...

For the TV station in Baton Rouge, Louisiana, see WVLA-TV. Radio station in Pennsylvania, United StatesWRBTHarrisburg, PennsylvaniaUnited StatesBroadcast areaHarrisburg–Carlisle metropolitan statistical areaSouth Central PennsylvaniaFrequency94.9 MHz (HD Radio)BrandingBob 94.9ProgrammingLanguage(s)EnglishFormatCountrySubchannelsHD2: Amy (Adult album alternative)AffiliationsPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsWHKFWHPWLANWLAN-FMWRVVWTKTHistoryFirs...

British theoretical physicist (1929–2024) Peter HiggsCH FRS FRSE HonFInstPHiggs in 2013BornPeter Ware Higgs(1929-05-29)29 May 1929Newcastle upon Tyne, EnglandDied8 April 2024(2024-04-08) (aged 94)Edinburgh, ScotlandAlma materKing's College London (BSc, MSc, PhD)Known for Higgs boson Higgs field Higgs mechanism Spontaneous symmetry breaking Spouse Jody Williamson (m. 1963; div. 1972)Children2Awards Hughes Medal (1...
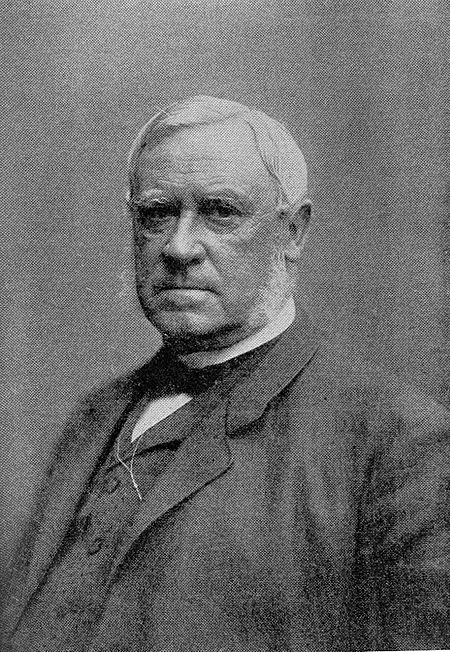
First Prime Minister of SwedenFor Louis Gerard De Geer's son, Gerard Louis De Geer, also a Prime Minister of Sweden, see Gerhard Louis De Geer. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Louis Gerhard De Geer – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove thi...

Naval battle near Tripoli, Libya Action of 16 May 1797A painting of the engagement by Terkild Emanuel LønningDate16 May 1797LocationOff Tripoli, TripolitaniaResult See aftermathBelligerents Denmark–Norway TripolitaniaCommanders and leaders Steen Bille Yusuf KaramanliStrength 1 frigate 1 brig 1 xebec 3 xebecs 3 smaller vesselsCasualties and losses Unknown Unknown The Action of 16 May 1797 was a naval battle that took place near Tripoli in Ottoman Tripolitania (present-day Libya). The Danish...

Fußball-Regionalliga 2003-2004Fußball-Regionalliga 2003-2004 Competizione Regionalliga Sport Calcio Edizione 10ª Organizzatore DFB Luogo Germania Partecipanti 36 Formula 2 gironi all'italiana Risultati Promozioni Rot-Weiss Essen Dinamo Dresda Rot-Weiß Erfurt Saarbrücken Retrocessioni Wattenscheid 09 Schalke 04 II Sachsen Lipsia Neumünster Schweinfurt 05 Eschborn Kaiserslautern II Cronologia della competizione 2002-2003 2004...

Sant'Epeneto Vescovo NascitaEfeso, I secolo d.C. MorteCartagine, 30 luglio I secolo d.C. Venerato daChiesa Cattolica, Chiesa Greco-ortodossa Ricorrenza30 luglio Manuale Epeneto di Cartagine (in greco antico: Ἐπαινετός?, Epainetós; Efeso, I secolo – Cartagine, 30 luglio I secolo) è stato, secondo alcune tradizioni non confermate storicamente, il primo vescovo di Cartagine.[1] È commemorato dalla Chiesa greco-ortodossa alle date del 4 gennaio, assieme ai Settan...

German astronomer For other people with similar names, see Johan Fabricius (disambiguation) and Johan Christian Fabricius. Johann Goldsmid,[1] better known by his Latinized name Johann(es) Fabricius (8 January 1587 – 19 March 1616),[2] eldest son of David Fabricius (1564–1617), was a Frisian/German astronomer and a modern era discoverer of sunspots in 1611, preceded by Thomas Harriot and followed by Galileo Galilei.[3] Biography Johannes was born in Resterhafe (Eas...































