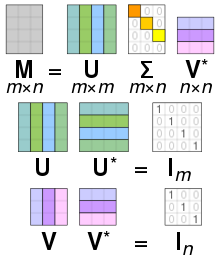
Сингулярний розклад матриці
|
Read other articles:

Ed Davey Sir Edward Jonathan Davey FRSA MP (lahir 25 Desember 1965) adalah seorang politikus Inggris yang menjabat sebagai Ketua Partai Liberal Demokrat sejak 2019. Davey sebelumnya menjabat dalam koalisi Cameron–Clegg sebagai Menteri Energi dan Perubahan Iklim dari 2012 sampai 2015 Referensi Pranala luar Wikiquote memiliki koleksi kutipan yang berkaitan dengan: Ed Davey. Wikimedia Commons memiliki media mengenai Ed Davey. Situs web resmi Profile Diarsipkan 2008-09-29 di Wayback Machine...

American military officer and planter (1742-1786) This article is about the American Revolutionary War general. For other people with a similar name, see Nathaniel Greene. Nathanael Greene1792 portrait of Greene by John TrumbullNickname(s)The Savior of the South The Fighting QuakerBornAugust 7 [O.S. July 27] 1742Colony of Rhode Island and Providence Plantations, British AmericaDiedJune 19, 1786(1786-06-19) (aged 43)Mulberry Grove, Georgia, United StatesBuriedSavannah, G...

Currency of the Kingdom of Lombardy–Venetia Lombardo-Venetian liralira austriaca (Italian) UnitSymbol£DenominationsSubunit 1⁄100centesimoCoinsc.1, c.3, c.5, c.10, c.15 £1⁄4, £1⁄2, £1, ₤3, £6 Rarely used£20, £40DemographicsOfficial user(s) Lombardy–VenetiaUnofficial user(s) Austria (silver coins)IssuanceMintMilan Mint, Venice Mint, Vienna MintValuationPegged by1⁄3 of Austrian florinThis infobox shows the latest status before thi...

Cet article est une ébauche concernant le monde colonial. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les colonies de peuplements (territoire colonial dans lequel sont installés beaucoup de métropolitains) on observe deux politiques : Architecture coloniale à Bandoung, 1910-1935 (île de Java, alors possession néerlandaise) ; bureau d'architectes Biezeveld & Moojen. Assimilation colon...

Divingat the Games of the XXVII OlympiadVenueSydney International Aquatic CentreDate22–30 September 2000No. of events8Competitors157 from 42 nations← 19962004 → Diving at the2000 Summer Olympics3 m springboardmenwomen10 m platformmenwomenSynchronized3 m springboardmenwomenSynchronized10 m platformmenwomenvte At the 2000 Summer Olympics in Sydney, eight diving events were contested for the first time due to the inclusion of synchronized variants for each of t...

Congresso della Repubblica Il Campidoglio Nazionale, sede del Congresso della Colombia. Stato Colombia TipoBicamerale Camere Camera dei rappresentanti Senato della Repubblica Istituito1991 daAssemblea Nazionale Costituente per la Costituzione del 1991 Presidente del SenatoRoy Barreras (PH) Presidente della CameraDavid Racero (PH) Ultima elezione13 marzo 2022 Prossima elezione2026 Numero di membri296 (108 senatori; 100 circoscrizioni nazionali, 2 circoscrizioni speciali indigene, 5 F...

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to the following WikiProjects:Trains Trains Portal This template is within the scope of WikiProject Trains, an attempt to build a comprehensive and detailed guide to rail transport on Wikipedia. If you would like to participate, you can visit the project page, where you can join the project and/or contribute to the discussion. See also: WikiProject Trains to do list and the Trains Portal.TrainsW...

Putri untuk PangeranGenre Drama Roman Remaja Fantasi Komedi PembuatMNC PicturesSkenarioAviv ElhamSutradaraRudi AryantoPemeran Ranty Maria Verrel Bramasta Fero Walandouw Rowiena Umboh Evan Marvino Penggubah lagu temaPotret, Andmesh Kamaleng & Ari LassoLagu pembuka Bagaikan Langit oleh Potret (Eps. 1—450) Tiba-Tiba oleh Andmesh Kamaleng (Eps. 451—659) Malaikat Itu Nyata oleh Ari Lasso (Eps. 660—687) Lagu penutup Bagaikan Langit oleh Potret (Eps. 1—450) Tiba-Tiba oleh Andmesh Kamale...

中国人民解放军新疆军区中国人民解放军陆军军旗存在時期1949年 - 1979年(首设)1985年至今(复设)國家或地區 中华人民共和国部門中国人民解放军陆军種類中国人民解放军陆军直属副战区级军区功能新疆地区的边境防卫,新疆军区的征兵动员規模副战区级规模直屬中国人民解放军陆军总部(管理)中央军委国防动员部(国防动员) 中国人民解放军西部战区(作战)駐�...

County in Oklahoma, United States Not to be confused with Texas County, Missouri. County in OklahomaTexas CountyCountyTexas County Courthouse in Guymon (2012)Location within the U.S. state of OklahomaOklahoma's location within the U.S.Coordinates: 36°45′N 101°29′W / 36.75°N 101.48°W / 36.75; -101.48Country United StatesState OklahomaFounded1907Named forTexasSeatGuymonLargest cityGuymonArea • Total2,049 sq mi (5,310 km2) ...
This article is about the debate over responsibility for World War I. For the notion of collective guilt for the Holocaust, see German collective guilt. European diplomatic alignments shortly before the war. The Ottomans joined with Germany shortly after the war started. Italy remained neutral in 1914 and joined the Entente in 1915. Part of a series on the History of Germany Topics Chronology Historiography Military history Economic history Healthcare Islam LGBT history Jewish history Women's...

Skala vernier atau skala nonius adalah bantuan penglihatan yang memungkinkan pengguna untuk mengukur lebih tepat daripada yang bisa dilakukan tanpa bantuan saat membaca skala pengukuran lurus atau sirkular yang terbagi rata. Ini adalah skala yang menunjukkan di mana pengukuran terletak di antara dua skala pada skala utama, digunakan untuk meningkatkan ketelitian dan menguranggi ketidakpastian dalam pengukuran. Vernier biasa digunakan pada sekstan yang digunakan dalam navigasi, alat ilmiah ya...

Indonesian pickled vegetable or fruit dish This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Asinan – news · newspapers · books · scholar · JSTOR (October 2015) (Learn how and when to remove this message) AsinanAsinan Betawi topped with yellow kerupuk mieCourseSnackPlace of originIndonesiaRegion or stateJakart...

Jinan YaoqiangInternational Airport济南遥墙国际机场IATA: TNAICAO: ZSJNInformasiJenisPublicMelayaniJinan, ShandongLokasiYaoqiang Subdistrict, Distrik Licheng, JinanMaskapai penghubungShandong AirlinesKetinggian dpl23 mdplKoordinat36°51′26″N 117°12′58″E / 36.85722°N 117.21611°E / 36.85722; 117.21611Situs webwww.jnairport.comPetaCAAC airport chartTNALocation of airportLandasan pacu Arah Panjang Permukaan m kaki 01/19 3,601 11,814 Beton Statis...

لا شون فورد (بالإنجليزية: La Shawn K. Ford) معلومات شخصية الميلاد العقد 1970 شيكاغو مواطنة الولايات المتحدة مناصب عضو مجلس نواب إلينوي تولى المنصب10 يناير 2007 الحياة العملية المدرسة الأم جامعة لويولا شيكاغو المهنة سياسي الحزب الحزب الديمقراطي الل�...

2021-22シーズンのデンバー・ナゲッツヘッドコーチ マイケル・マローンGM カルビン・ブースオーナー アン・ウォルトン・クロエンケ(英語版)アリーナ ボール・アリーナ 成績シーズン成績 48勝34敗(勝率.585)順位 ディビジョン : 2位 (ノースウェスト)カンファレンス : 6位 (ウェスタン)プレーオフ成績 1回戦(GSWに1–4で敗退) スタッツ@ Basketball-Reference.com地元メデ�...

Consonantal sound represented by ⟨b⟩ in IPA Voiced bilabial plosivebIPA Number102Audio sample source · helpEncodingEntity (decimal)bUnicode (hex)U+0062X-SAMPAbBraille The voiced bilabial plosive or stop is a type of consonantal sound used in many spoken languages. The symbol in the International Phonetic Alphabet that represents this sound is ⟨b⟩, and the equivalent X-SAMPA symbol is b. The voiced bilabial stop occurs in English, and it is the sound den...
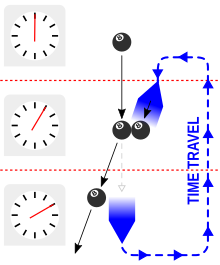
Theoretical paradox resulting from time travel This article is about apparent contradictions in the concept of time travel. For the controversy over the origin of birds, see temporal paradox (paleontology). A temporal paradox, time paradox, or time travel paradox, is a paradox, an apparent contradiction, or logical contradiction associated with the idea of time travel or other foreknowledge of the future. While the notion of time travel to the future complies with the current understanding of...

Location of Spisska District in the Košice Region Hnilčík (Hungarian: Szepespatak) is a village and municipality in the Spišská Nová Ves District in the Košice Region of central-eastern Slovakia. History In historical records the village was first mentioned in 1315. Geography The village lies at an altitude of 608 metres and covers an area of 23.23 km2. In 2011 Hnilčík had a population of 543 inhabbittants. Genealogical resources The records for genealogical research are availab...

سابليتي الإحداثيات 41°38′35″N 89°13′50″W / 41.6431°N 89.2306°W / 41.6431; -89.2306 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة لي خصائص جغرافية المساحة 4.12 ميل مربع عدد السكان عدد السكان 380 (1 أبريل 2020)[3] الكثافة السكا�...