Обернене число
| |||||||||
Read other articles:

Carik Kenangan dari Kepulauan Faroe, di mana perangko membentuk bagian dari gambar yang lebih besar. Carik Kenangan (bahasa Inggris: souvenir sheet) adalah sehelai kertas dengan prangko di dalamnya. Ukuran kertas ini lebih besar dari prangkonya, tepinya tidak bergerigi. Tetapi prangko di dalamnya dapat berperforasi, ada pula yang tidak berperforasi, ada pula yang model perekat, tinggal diangkat prangkonya saja, lalu ditempel pada sampul pos. Dapat dipergunakan untuk pemrangkoan, tetapi lebih ...

Ketanji Brown Jackson, 116th Associate Justice of the U.S. Supreme Court, clerked for her predecessor Justice Stephen Breyer during the 1999–2000 term. Law clerks have assisted the justices of the United States Supreme Court in various capacities since the first one was hired by Justice Horace Gray in 1882.[1] Each justice is permitted to have between three and four law clerks per Court term. Most persons serving in this capacity are recent law school graduates (and typically gradu...

Soleh SolihunSoleh di acara Ini TalkshowLahir2 Juni 1979 (umur 44)Bandung, Jawa Barat, IndonesiaAlmamaterUniversitas Padjajaran (1997—2004)PekerjaanAktorpenulissutradarajurnalispenyiar radiopelawak tunggalpresenterTahun aktif2004—sekarangSitus webSitus web resmiTanda tangan Soleh Solihun, S.I.Kom. (lahir 2 Juni 1979) adalah aktor, penulis, sutradara, jurnalis, penyiar radio, pelawak tunggal, dan presenter Indonesia. Sebagai jurnalis, ia bekerja di Trax, Playboy Indonesia, dan R...

Human settlement For the village in Azerbaijan, see Kültəpə. For other uses, see Kültepe (disambiguation). KültepeHittite palace at KültepeShown within TurkeyLocationKayseri Province, TurkeyRegionAnatoliaCoordinates38°51′N 35°38′E / 38.850°N 35.633°E / 38.850; 35.633TypeSettlementHistoryCulturesHittite AssyrianSite notesConditionIn ruins Kültepe (Turkish: lit. ash-hill), also known as Kanesh or Nesha, is an archaeological site in Kayseri Province, Turkey...

Disambiguazione – Se stai cercando altri significati, vedi Nick Fury (disambigua). Nick FuryNick Fury, disegnato da Jim Steranko. UniversoUniverso Marvel Lingua orig.Inglese AutoriStan Lee Jack Kirby EditoreMarvel Comics 1ª app.maggio 1963 1ª app. inSgt. Fury and his Howling Commandos (vol. 1[1]) n. 1 Editore it.Le Maschere 1ª app. it.15 ottobre 1966 1ª app. it. inIl Serg. Fury e i suoi commandos n. 1 Caratteristiche immaginarieNome completoNicholas Joseph ...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Bagian dari seri tentangBuddhisme SejarahPenyebaran Sejarah Garis waktu Sidang Buddhis Jalur Sutra Benua Asia Tenggara Asia Timur Asia Tengah Timu...

Asteroid and near-Earth object 2100 Ra-ShalomShape model of Ra-Shalom from its lightcurveDiscovery [1]Discovered byE. F. HelinDiscovery sitePalomar Obs.Discovery date10 September 1978DesignationsMPC designation(2100) Ra-ShalomPronunciation/ˌrɑː ʃəˈloʊm/[2]Named afterRa and Shalom(composed name)[3]Alternative designations1978 RA · 1975 TBMinor planet categoryNEO · Aten [1][4]Orbital ...

Три внутренних галилеевых спутника вращаются в резонансе 4:2:1 Сравнение галилеевых спутников с Юпитером. Сверху вниз: Ио, Европа, Ганимед и Каллисто Прибор середины XVIII века, демонстрирующий орбиты спутников Юпитера Сравнение с Землёй и Луной Юпитер со спутниками (объе...

Д. Э. Милле - Роялист вне закона, 1853 Проскри́пция (лат. proscriptio от proscribere — «письменно обнародовать, оглашать») — в Древнем Риме — список лиц, объявленных вне закона. За выдачу или убийство включённого в списки назначалась награда, за укрывательство — казнь. Иму...

1945–1950 Parliament of the United Kingdom ←1935–1945 Parliament 1950–1951 Parliament→Palace of Westminster in 1945OverviewLegislative bodyParliament of the United KingdomTerm26 July 1945 (1945-07-26) – 23 February 1950 (1950-02-23)Election1945 United Kingdom general electionGovernmentFirst Attlee ministry House of CommonsMembers640SpeakerDouglas Clifton Brown LeaderHerbert MorrisonJames Chuter Ede Prime MinisterClement At...

Angkak Angkak (Hanzi: 紅麴米, 红曲米; pinyin: hóng qú mǐ; lit. red yeast rice), red fermented rice, red kojic rice, red koji rice, atau ang-kak, yaitu beras putih jenis tertentu yang dibiakkan dengan sejenis ragi khusus selama beberapa hari sehingga mengubah warna beras menjadi merah. Angkak telah dikenal penduduk Tiongkok sejak ratusan tahun silam, dan umum digunakan orang Tionghoa sebagai bagian dari campuran rempah masakan dan herbal kesehatan mereka. Di Amerika, angkak yang d...

The Signpost Volume 20Issue 94 July 2024 ? – CC0News and notesWMF board elections and fundraising updatesThree new admins, but overall numbers still shrinking. Rijksmuseum – CC0Special reportWikimedia Movement Charter ratification vote underway, new Council may surpass power of BoardWill we weather the storm? MBH – CC BY-SA 4.0In focusHow the Russian Wikipedia keeps it clean despite having just a couple dozen administratorsUnbundling, automation, fighting spirit, and a bot named Reimu ...
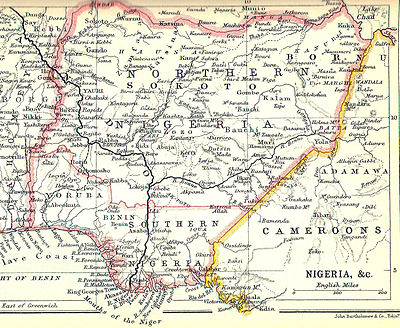
British protectorate from 1900 to 1914 See also: Northern Region, Nigeria Northern Nigeria Protectorate1900–1914 Ensign Badge Anthem: God Save the KingNorthern Nigeria (red)British possessions in Africa (pink)1913StatusProtectorate of British EmpireCapitalZungeruCommon languagesEnglish (official)Hausa, Arabic, Yoruba, Fula, Kanuri widely spokenReligion Islam, Christianity, Yoruba religion, African traditional religionGovernmentConstitutional monarchyMonarch • 1900...

Russian politician In this name that follows Eastern Slavic naming customs, the patronymic is Borisovich and the family name is Senin. Vladimir SeninMPВладимир СенинMember of the State Duma (Party List Seat)IncumbentAssumed office 12 October 2021 Personal detailsBorn (1960-09-17) 17 September 1960 (age 63)Moscow, RSFSR, USSRPolitical partyUnited RussiaEducationMoscow Institute of ManagementMoscow State Law Academy Vladimir Borisovich Senin (Russian: Владимир ...

包联制,又称包联责任制,是一个广义的社会治理概念,包联一词中“包”即总揽全责,“联”即联络、连带[1]。包联制中的负责人被称为包联人、包联责任人或包联干部。该制度在中国内地的精准扶贫、应对2019冠状病毒病疫情等基层社会治理实践中有所使用。 内涵与外延 包联制这一概念提出于21世纪初[原創研究?],与经济生产领域的“大包干”、承包制、中国国�...

2022 FIFA World Cup qualification (CONCACAF)Tournament detailsDates24 March 2021 – 30 March 2022Teams34 (from 1 confederation)Tournament statisticsMatches played118Goals scored345 (2.92 per match)Attendance999,020 (8,466 per match)Top scorer(s) Cyle Larin(13 goals)← 2018 2026 → International football competition CONCACAF Qualifiers FIFA World CupCCCF–NAFC era 1950 1954 1958 1962 CONCACAF era 1966 1970 1974 1978 1982 1986 1990 1994 1998 2002 2006 2010 2014 ...

Generic medieval Western European name for eastern gold coins Crusader coins of the Kingdom of Jerusalem: Denier in European style with Holy Sepulchre (1162–75); Kufic gold bezant (1140–1180); gold bezant with Christian symbol (1250s) (British Museum). Gold coins were first copied dinars and bore Kufic script, but after 1250 Christian symbols were added following Papal complaints. County of Tripoli gold bezant in Arabic (1270–1300), and Tripoli silver gros (1275–1287). British Museum....

Roberto PiccoliRoberto Piccoli con il Cagliari nel 2024Nazionalità Italia Altezza190 cm Peso78 kg Calcio RuoloAttaccante Squadra Cagliari CarrieraGiovanili 2012-2014 Tritium2014-2020 Atalanta Squadre di club1 2018-2020 Atalanta3 (0)2020-2021→ Spezia20 (5)2021-2022 Atalanta12 (1)2022→ Genoa5 (0)2022-2023→ Verona7 (0)2023→ Empoli13 (2)2023-2024→ Lecce35 (5)2024-→ Cagliari3 (2) Nazionale 2016 Italia U-154 (0)2016-2017...

Duke of Swabia, King of Jerusalem and King of Sicily (1252–1268) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2011) (Learn how and when to remove this message) ConradinKing Conrad the Younger, from theCodex Manesse (Folio 7r), c. 1304King of JerusalemReign21 May 1254 – 29 October 1268PredecessorConrad IISuccessorHugh IKing of SicilyReign2...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vieux Lyon – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) UNESCO World Heritage Site in Auvergne-Rhône-Alpes, France Historic Site of LyonUNESCO World Heritage SiteLocationLyon, Arrondissement of Lyon, ...












