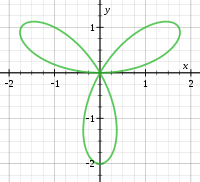
Singular point of a curve
|
Read other articles:

تصوير وعائي دماغي تصوير وعائي دماغي يُظهر إسقاط مُستعرض للدورة الفقارية القاعدية والمخية الخلفية تعديل مصدري - تعديل تصوير وعائي دماغي[1] أو تصوير الأوعية الدماغية[1] (بالإنجليزية: Cerebral angiograph) هي شكل من تصوير الأوعية، حيثُ تساعد في تصوير الأوعية الدموية في وحول

Fannie B. LindermanBornFannie Beatrice FryAugust 1875Winscombe, Somerset, EnglandDiedOctober 9, 1960Rockford, Illinois, U.S.Other namesLady LindPoet of the CommonplaceOccupationseducatorentertainerwriterSpouses William Cordova Linderman (m. 1891; died 1936) Benjamin Harling (m. 1943; died 1946)Children1Signature Fannie B. Linderman (née, Fry; after first marriage, Linderman; after sec...

Football league seasonFootball League play-offsSeason2012–13ChampionsCrystal Palace(Championship)Yeovil Town(League One)Bradford City(League Two)Matches played15Goals scored36 (2.4 per match)Biggest home winWatford 3–1 Leicester(Championship)Biggest away winBurton 1–3 Bradford(League Two)Highest scoringBrentford 3–3 Swindon(6 goals)Highest attendance82,025 – Crystal Palace v Watford(Championship Final)Lowest attendance5,955 – Cheltenham v Northampton(League Two semi-final)Ave...

Former dynasty of India AyAy Kingdom in 1st Century CECapital Podhigai Malai (early historic) Vizhinjam (medieval) Common languagesOld Tamil , malayalamReligion Hinduism Succeeded by Venad (historical region) Ay was a dynasty which controlled the south-western tip of the Indian peninsula, from the early historic period up to the medieval period.The clan traditionally held sway over the port of Vizhinjam, the fertile region of Nanjinad, and southern parts of the spice-producing Western Gh...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gatineau Hot Air Balloon Festival – news · newspapers · books · scholar · JSTOR (April 2014) (Learn how and when to remove this template message) 250pxl The Gatineau Hot Air Balloon Festival (French: Festival de Montgolfières de Gatineau) is an annual festival...

Indian State Government Government of BiharBicameralSeat of GovernmentPatnaCountryIndiaLegislative branchAssemblyBihar Legislative AssemblySpeaker, Bihar Vidhan SabhaAwadh Bihari ChoudharyDeputy Speaker, Bihar Vidhan SabhaMaheshwar HazariMembers in Assembly243CouncilBihar Legislative CouncilChairman of Bihar Vidhan ParishadDevesh Chandra ThakurDeputy ChairRam Chandra PurveMembers in Council75 (63 Elected + 12 Nominated)Executive branchGovernorRajendra ArlekarChief MinisterNitish KumarDeputy C...

Mathematical result of division For other uses, see Quotient (disambiguation). The quotient of 12 apples by 3 apples is 4. Arithmetic operationsvte Addition (+) term + term summand + summand addend + addend augend + addend } = {\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{term}}\,+\,{\text{term}}\\\scriptstyle {\text{summand}}\,+\,{\text{summand}}\\\scriptstyle {\text{addend}}\,+\,{\text{addend}}\\\scriptstyle {\text{augend}}\,+\,{\text{addend}}\end{matrix}}\right\}\,=\...

Сілвіу Ізворану Особисті дані Народження 3 грудня 1983(1983-12-03) (39 років) Галац, Румунія Зріст 186 см Вага 79 кг Громадянство Румунія Позиція захисник Інформація про клуб Поточний клуб завершив кар'єру Юнацькі клуби 2003 «Дуніря» (Галац) Професіональні клуби* Роки Клуб Іг...

Australian rugby league footballer Ben RidgeRidge playing for the Titans in 2011.Personal informationBorn (1989-12-13) 13 December 1989 (age 33)Toowoomba, Queensland, AustraliaPlaying informationHeight186 cm (6 ft 1 in)Weight102 kg (16 st 1 lb)PositionSecond-row, Lock Club Years Team Pld T G FG P 2010–15 Gold Coast Titans 58 1 0 0 4 Source: Rugby League Project Ben Ridge (born 13 December 1989) is an Australian former professional rugby league football...

British pharmacologist (born 1958) Peter ElliottBornPeter John Elliott (1958-08-19) August 19, 1958 (age 65)Cardiff, WalesNationalityBritishAlma materLondon University (Chelsea College)Cambridge University (Trinity College)Scientific careerFieldsPharmacology, Drug DevelopmentInstitutionsWapiti Pharmaceutical Consulting Peter Elliott (born August 19, 1958) is a British pharmacologist and drug developer who has initiated clinical trials across a range of disease areas, and is the co-d...

2012 mixtape by Le1fDark YorkMixtape by Le1fReleasedApril 9, 2012 (2012-04-09)GenreHip hopLength66:07LabelGreedheadCamp & StreetProducerLe1fBoodyTom RichmanCybergigaNguzunguzuMorris5kinandbone5Matt ShadetekLe1f chronology Dark York(2012) Liquid(2012) Dark York is the first mixtape by American rapper and producer Le1f. It was released on Greedhead Music and Camp & Street on April 9, 2012.[1] Critical reception Professional ratingsReview scoresSourceRating...

This article is about a local government authority. For the suburb, see Kalamunda, Western Australia. Local government area in Western AustraliaCity of KalamundaWestern AustraliaThe City of Kalamunda within the Perth Metropolitan AreaPopulation58,762 (LGA 2021)[1]Established1897Area324.2 km2 (125.2 sq mi)MayorMargaret Thomas[2]Council seatKalamundaRegionEastern Metropolitan Perth Darling ScarpState electorate(s)Darling Range, Forrestfield, KalamundaFederal divis...

Ere rabbiniche Zugot Tannaim Amoraim Savoraim Gaonim Rishonim Acharonim Tsiyun (tombe/memoriali) di Rabbeinu Behayé e i suoi talmidim, `Hokok nella Galil, Israele Bahye ben Asher ibn Halawa noto anche come Rabbeinu Behaye in ebraico רבינו בחיי? (Saragozza, XIII secolo – 1340) è stato un rabbino e religioso spagnolo, studioso dell'Ebraismo, commentatore del Tanakh (Bibbia ebraica) e rinomato per aver introdotto la Cabala (misticismo ebraico) nello studio della Torah. Consid...

2000 studio album by MewHalf the World Is Watching MeStudio album by MewReleased4 May 2000RecordedFebruary–August 1999GenreAlternative rock, indie popLength43:39LabelEvil OfficeProducerMewMew chronology A Triumph for Man(1997) Half the World Is Watching Me(2000) Frengers(2003) Singles from Half the World Is Watching Me King ChristianReleased: February 2000 Her Voice Is Beyond Her YearsReleased: June 2000 MicaReleased: January 2001 Professional ratingsReview scoresSourceRatingGaffa l...

1937 film by Jack Conway SaratogaTheatrical posterDirected byJack ConwayScreenplay byAnita LoosRobert HopkinsStory byAnita LoosRobert HopkinsProduced byBernard H. HymanStarringClark GableJean HarlowCinematographyRay JuneEdited byElmo VeronMusic byEdward WardProductioncompanyMetro-Goldwyn-MayerDistributed byLoew's Inc.Release date July 23, 1937 (1937-07-23) Running time92 minutesCountryUnited StatesLanguageEnglishBudget$1.1 million[1]Box office$3.252 million (worldwide r...

Николай ЯрмольчукНиколай Григорьевич Ярмольчук Дата рождения 1898(1898) Место рождения деревня Любань, Российская империя (ныне: Ровенская область, Украина) Дата смерти апрель 1979 Место смерти Москва, СССР Гражданство Российская империя → СССР Род деятельност...

Iranian training aircraft Yasin HESA Yasin Role Military trainer aircraft / Jet trainerType of aircraft National origin Iran[1][2][3][4] Manufacturer HESA Designer Iran Aviation Industries Organization and Islamic Republic of Iran Air Force First flight 2019 Introduction 11 March 2023 Status In production Primary user IRIAF Number built 2 The HESA Yasin (Persian: یاسین) is an Iranian training jet which was unveiled on October 17, 2019. The jet might a...

1228–1229 attempted conquest of the Holy Land Sixth CrusadePart of the CrusadesFrederick II (left) meets al-Kamil (right)Date1227–1229LocationNear EastResult Crusader victory Jerusalem given back to the CrusadersTerritorialchanges Jerusalem, Nazareth, Sidon, Jaffa and Bethlehem relinquished to Crusaders.Belligerents Holy Roman EmpireTeutonic KnightsKingdom of Sicily Ayyubids of EgyptAyyubids of DamascusCommanders and leaders Frederick IIHermann of SalzaThomas of AquinoPeter des RochesWill...

Style of architecture used in French colonies This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) The Presidential Palace of Vietnam, i...

DatokaramaLahirAbdullah RaqieMinangkabauMeninggalAbad 17Kampung Lere, Palu, Sulawesi TengahNama lainDatuk KaramaPekerjaanUlamaDikenal atasPenyebar Islam di Tanah Kaili, Sulawesi TengahSuami/istriIntje DilleAnakIntje Dongko Intje Saribanu Datokarama adalah tokoh pembawa pertama agama Islam di lembah Palu dan menjadi nama perguruan tinggi STAIN Datokarama Palu.[1] Datokarama memiliki nama asli Syekh Abdullah Raqie, seorang tokoh yang berasal dari Pagaruyung, yang pertama kali meny...