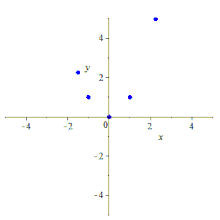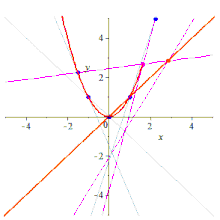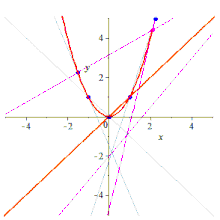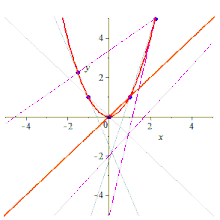
Five points determine a conic
|
Read other articles:

Jagadish ShettarJagadish Shettar pada 2006' Ketua Menteri Karnataka ke-21Masa jabatan12 Juli 2012 – 8 Mei 2013GubernurHansraj Bhardwaj PendahuluD. V. Sadananda GowdaPenggantiSiddaramaiahDaerah pemilihanHubli-Dharwad central Informasi pribadiLahirJagadish Shivappa Shettar17 Desember 1955 (umur 68)Kerura, distrik Bagalkot, KarnatakaPartai politikPartai Bharatiya JanataSuami/istriShilpa ShettarAnak2 putraSitus webJagdish ShettarPer tanggal 8 Mei, 2013Sunting kotak info �...

Stadio Fratelli BallarinFossa dei Leoni Vista della gradinata Sud dello stadio Informazioni generaliStato Italia UbicazioneV. F. Morosini 27, I-63074 S. Benedetto del Tronto Inaugurazione1931 ProprietarioComune di San Benedetto del Tronto Intitolato aAldo BallarinDino Ballarin Informazioni tecnicheStrutturaPianta rettangolare Mat. del terrenoTerra Dim. del terreno105 × 68 m Mappa di localizzazione Modifica dati su Wikidata · ManualeCoordinate: 42°57′34.68″N 13°52′53.7...

Argentine rock band This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Babasónicos – news · newspapers · books · scholar · JSTOR (April 2016) (Learn how and when to remove this template message) BabasónicosBackground informationOriginBuenos Aires, Lanús, ArgentinaGenresAlternative rock, pop rock, rock, psych...

American academic and college president Arthur S. Adams8th President of the University of New HampshireIn office1948–1950Preceded byHarold W. StokeSucceeded byRobert F. Chandler Personal detailsBorn(1896-07-01)July 1, 1896Winchester, Massachusetts, USDiedNovember 18, 1980(1980-11-18) (aged 84)Concord, New Hampshire, USAlma materUnited States Naval AcademyUniversity of California, BerkeleyColorado School of Mines Arthur Stanton Adams (July 1, 1896 – November 18, 1980) was an American ...

Struck metal pendant medallion, or a coin made in imitation of these This article is about the jewelry item. For the botanical term indicating - having bracts, see Bract. Bracteate DR BR42 bearing the inscription Alu and a figure on a horse A bracteate (from the Latin bractea, a thin piece of metal) is a flat, thin, single-sided gold medal worn as jewelry that was produced in Northern Europe predominantly during the Migration Period of the Germanic Iron Age (including the Vendel era in Sweden...

Untuk album dengan nama yang sama, lihat: Miracle, yang dirilis pada tahun 2008. MiracleAlbum studio karya BoADirilis24 September 2002Direkam2002 (kompilasi singel)GenrePopDurasi?LabelSM EntertainmentProduserLee Soo Man (?)Kronologi BoA Peace B. Remixes(2002)Peace B. Remixes2002 Miracle(2002) Valenti(2003)Valenti2003 Miracle adalah mini album ke 2 BoA yang meriliskan kembali beberapa lagu berbahasa Jepang dan direkam kembali dalam bahasa Korea. Lagu Lagu promosional dicetak tebal. 기적 ...

Dungeons & Dragons sourcebook The original 1987 edition of the Forgotten Realms Campaign Set The Forgotten Realms Campaign Setting is a role-playing game sourcebook first published by TSR in 1987 for the first edition of the fantasy role-playing game Advanced Dungeons & Dragons that describes the campaign setting of the Forgotten Realms. It contains information on characters, locations and history. Various revised and updated editions have been produced over the years. 1st edition Con...

Pour les articles homonymes, voir Aardvark. General Dynamics F-111F Constructeur General Dynamics Rôle bombardier Premier vol 21 décembre 1964 Mise en service 1967 Date de retrait 1998 aux États-Unis et 2010 en Australie Nombre construits 554 Variantes ou dérivés General Dynamics–Grumman F-111B General Dynamics F-111C General Dynamics EF-111A Raven General Dynamics F-111K Équipage 2 (1 pilote, 1 officier des systèmes d'armes) Motorisation Moteur Pratt & Whitney TF30-P-100 Nombre...

Scottish Division One 1958-1959 Competizione Scottish Division One Sport Calcio Edizione 62ª Organizzatore SFL Date dal 20 agosto 1958al 21 aprile 1959 Luogo Scozia Partecipanti 18 Formula Girone all'italiana A/R Risultati Vincitore Rangers(31º titolo) Retrocessioni FalkirkQueen of the South Statistiche Miglior marcatore Joe Baker (25) Incontri disputati 306 Gol segnati 1 195 (3,91 per incontro) Cronologia della competizione 1957-58 1959-60 Manuale La Scottish ...

2019 single by Alicia Keys Time MachineSingle by Alicia Keysfrom the album Alicia ReleasedNovember 20, 2019 (2019-11-20)Genre R&B funk Length4:30LabelRCASongwriter(s)Alicia KeysSebastian KoleRob KnoxProducer(s)KeysRob KnoxEmile Haynie (co)Alicia Keys singles chronology Show Me Love (2019) Time Machine (2019) Underdog (2020) Music videoTime Machine on YouTube Time Machine is a song by American singer and songwriter Alicia Keys. It was written by Keys, Sebastian Kole and Rob ...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Medical conditionNecrobiosis lipoidicaOther namesNecrobiosis lipoidica diabeticorumSpecialtyDermatology Necrobiosis lipoidica is a rare, chronic skin condition predominantly associated with diabetes mellitus (known as necrobiosis lipoidica diabeticorum or NLD).[1] It can also occur in individuals with rheumatoid arthritis or without any underlying conditions (idiopathic).[2] It is characterized by hardened, raised areas of the skin, often appearing on the shins, with a y...

Vince and Kath The first original image screenshot of Vince and Kath storyAuthorJenny Ruth AlmoceraCountryPhilippinesGenreRomancePublisherIndependentPublication date2 January 2016; 8 years ago (2016-01-02)Media typeDigital images Vince and Kath is an online romantic series written by Filipino author Jenny Ruth Almocera.[1][2] The story consists of screenshots of SMS and chat conversations between the characters with few narrative sections. Each album con...

Hills in England, Wales and Ireland over 2000 feet See also: Lists of mountains and hills in the British Isles HewittCalf Top in Cumbria, the smallest Hewitt which was confirmed in 2016 as almost exactly 2,000 ft.[a]Highest pointElevationover 2,000 ft (609.6 m)Prominenceover 30 m (98.4 ft)GeographyLocation 524 British Isles: 209 Ireland[b] 180 England 135 Wales This is a list of Hewitt mountains in England, Wales and Ireland by height. Hewitts are defi...

Campagnatico Apse of the بيفي of San Giovanni Battista. شعار Campagnaticoشعار Campagnaticoشعار الاسم الرسمي Comune di Campagnatico الإحداثيات 42°53′04″N 11°16′17″E / 42.884444444444°N 11.271388888889°E / 42.884444444444; 11.271388888889 [1] تقسيم إداري البلد إيطاليا[2] التقسيم الأعلى مقاطعة غروسيتو خصائص جغرافية &...

Top division in South Korean football For comprehensive South Korean professional football league including first division and second division, see K League. Football leagueK League 1Organising bodyK League FederationFounded1983; 41 years ago (1983)CountrySouth KoreaConfederationAFCNumber of teams12Level on pyramid1Relegation toK League 2Domestic cup(s)Korean FA CupInternational cup(s)AFC Champions League EliteAFC Champions League 2Current championsUlsan Hyundai (4th title) ...

Pro Wrestling IllustratedSampul Penghargaan Akhir Tahun PWI 2014 menampilkan Daniel BryanKategoriOlahragaFrekuensiBulananPenerbitKappa Publishing GroupTerbitan pertamaSeptember 1979NegaraAmerika SerikatBahasaBahasa InggrisSitus webwww.pwi-online.comISSN1043-7576Pro Wrestling Illustrated (PWI) adalah majalah gulat profesional Amerika Serikat yang dijual secara internasional yang didirikan pada tahun 1979 oleh penerbit Stanley Weston.[1] PWI berkantor pusat di Blue Bell, Pennsylvania, d...

1995 Japan-exclusive puzzle video game This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: O-Chan no Oekaki Logic – news · newspapers · books · scholar · JSTOR...

Culinary traditions of Apulia, Italy Italian cuisine History Ancient Roman cuisine Medieval cuisine Early modern cuisine Contemporary cuisine Regional cuisines Abruzzese cuisine Apulian cuisine Arbëreshë cuisine Corsican cuisine Ligurian cuisine Lombard cuisine Mantuan cuisine Lucanian cuisine Neapolitan cuisine Piedmontese cuisine Roman cuisine Sardinian cuisine Sicilian cuisine Venetian cuisine Lists Chefs Dishes Pasta Cheeses PDO Desserts and pastries Restaurants Wine IGT DOCG DOC Beer S...

2004 Georgian parliamentary election ← 2003 28 March 2004 2008 → 150 of the 235 seats in Parliament113 seats needed for a majority Party Leader % Seats NM–D Nino Burjanadze 67.75 153 Right Opposition David Gamkrelidze 7.74 23 SLP Shalva Natelashvili 6.14 4 DAK Aslan Abashidze 3.95 6 For a New Georgia Eduard Shevardnadze – 19 Abkhazians – – 10 Independent – – 20 This lists parties that won seats. See the complete results below. Prime Minister before Prime Min...






![{\displaystyle [x^{2}:xy:y^{2}:xz:yz:z^{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1902a3df10871523d42ac2a21cf4924de43786)
![{\displaystyle [A:B:C:D:E:F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58676be46552da77703fbfeb8fc14fda11841eb7)

![{\displaystyle [1:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb57ffba69005b439cb1dc8ba40df9c147bae5d2)
![{\displaystyle [0:1:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb225ddb544b9183ae37507e364ab290e5c14b8)