Brill–Noether theory
|
Read other articles:

Total length of a transport network In transport terminology, network length (or, less often, system length) refers to the total length of a transport network, and commonly also refers to the length of any fixed infrastructure associated with the network. A measurement can be made of the network length of various different modes of transport, including rail, bus, road and air. The measurement may focus on one of a number of specific characteristics, such as route length, line length or track ...

Final Piala Raja Spanyol 1929TurnamenPiala Raja Spanyol 1928–1929 RCD Español Real Madrid 2 1 Tanggal3 Februari 1929StadionStadion Mestalla, ValenciaWasitPelayo SerranoPenonton25.000← 1928 1930 → Final Piala Raja Spanyol 1929 adalah pertandingan final ke-27 dari turnamen sepak bola Piala Raja Spanyol untuk menentukan juara musim 1928–1929. Pertandingan ini diikuti oleh RCD Español dan Real Madrid dan diselenggarakan pada 3 Februari 1929 di Stadion Mestalla, Valencia. RCD Esp...
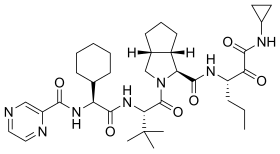
Chemical compound TelaprevirClinical dataTrade namesIncivek, IncivoAHFS/Drugs.comConsumer Drug InformationMedlinePlusa611038License data US FDA: Telaprevir Routes ofadministrationOral[1]ATC codeJ05AP02 (WHO) Legal statusLegal status US: ℞-only Pharmacokinetic dataProtein binding59–76% [2]Metabolismextensive hepaticElimination half-life9–11 hours [2]Excretion90% (bile), 9% (exhaled air), 1% (urine)Identifiers IUPAC name (1S,3aR,6aS)-2-[(2S...
Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman bahasa acak Bahasa Aram Asyur Baru ܐܬܘܪܝܐ ܣܘܪܝܝܐ Ātûrāyâ, ܣܘܪܝܬ ܣܘܪܝܝܐ Sûret, Ashuri, Suryaya, Sooreth Sûret dalam abjad Suryani Dituturkan diIrak, Suriah, Iran, TurkiWilayahUtara Irak, Hakkari Turkey, Urmia IranPenutur(232,300 per 1994)[1] Rumpun bahasaAfroasiatik SemitikSemitik TengahSemitik Barat Laut...

زمبرو تشيسيناو تأسس عام 1947 الملعب ملعب زيمبرو(السعة: 10,400) البلد مولدوفا الدوري الدوري المولدوفي الوطني الإدارة المدرب فلاد غويان (10 يونيو 2020–2021)فلاد غويان (26 يونيو 2022–)[1] الموقع الرسمي الموقع الرسمي الطقم الرسمي الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل...

Barnstable, Massachusetts, has more than 75 entries on the National Register of Historic Places. For listings elsewhere in Barnstable County, see National Register of Historic Places listings in Barnstable County, Massachusetts. Contents: Counties in Massachusetts Barnstable | Berkshire | Bristol | Dukes | Essex | Franklin | Hampden | Hampshire | Middlesex | Nantucket | Norfolk | Plymouth | Suffolk | Worcester This National Park Service list is compl...

American breed of domestic chicken Plymouth RockHens, barred plumageConservation statusrecoveringOther namesRockBarred RockCountry of originUnited StatesStandardAmerican Poultry AssociationUsedual-purpose breedTraitsWeightMale: Standard: minimum 3.4 kg (7.5 lb)[1]: 241 Bantam: maximum 1.4 kg (3 lb)[1]: 242 Female: Standard: minimum 2.9 kg (6.5 lb)[1]: 241 Bantam: maximum 1.1 kg (2.5 ...

لويس هارولد غراي (بالإنجليزية: Louis Harold Gray) معلومات شخصية الميلاد 10 نوفمبر 1905 [1][2] ريتشموند على نهر التايمز الوفاة 9 يوليو 1965 (59 سنة) [1][2] نورثوود [لغات أخرى] مواطنة المملكة المتحدة عضو في الجمعية الملكية الحياة العملية اختصار ...

Deke SlaytonLahirDonald Kent Slayton(1924-03-01)1 Maret 1924Sparta, Wisconsin, ASMeninggal13 Juni 1993(1993-06-13) (umur 69)League City, Texas, ASKebangsaanAmerika SerikatAlmamaterUniversitas Minnesota, B.S. 1949Penghargaan Collier TrophyJames H. Doolittle AwardKarier luar angkasaAntariksawan NASAPekerjaan sebelumnyaPilot pengebom, Pilot uji cobaPangkat Mayor, Angkatan Udara Amerika SerikatWaktu di luar angkasa9 hari 01 jam 28 menitLambang misiPensiun27 Februari 1982 Donald Kent Deke Sl...

У этого термина существуют и другие значения, см. Хозяйка. Хозяйкаукр. Хазяйка Жанр Мелодрама Режиссёр Бата Недич[1] В главных ролях Елена Стефанская, Екатерина Варченко, Марк Дробот, Сергей Радченко, Владимир Горянский Страна Украина Язык Русский Число сезонов ...

Pour les articles homonymes, voir Saint-Georges, Saint Georges (homonymie) et Georges. Saint-Georges-de-Rouelley La rue de l'Église. Administration Pays France Région Normandie Département Manche Arrondissement Avranches Intercommunalité Communauté d'agglomération Mont-Saint-Michel-Normandie Maire Mandat Raymond Bechet 2020-2026 Code postal 50720 Code commune 50474 Démographie Gentilé Saint-Georgeois Populationmunicipale 542 hab. (2021 ) Densité 26 hab./km2 Géographie Coo...

BagneuxcomuneBagneux – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementÉpernay CantoneVertus-Plaine Champenoise TerritorioCoordinate48°34′N 3°50′E48°34′N, 3°50′E (Bagneux) Superficie13,92 km² Abitanti498[1] (2009) Densità35,78 ab./km² Altre informazioniCod. postale51260 Fuso orarioUTC+1 Codice INSEE51032 CartografiaBagneux Modifica dati su Wikidata · Manuale Bagneux è un comune francese di 498 abitanti situa...

Fiamē Naomi MataʻafaFiamē Naomi Mataʻafa pada 2021 Perdana Menteri Samoa ke-7PetahanaMulai menjabat 24 Mei 2021[a]O le Ao o le MaloTuimalealiifano Va'aletoa Sualauvi IIWakilTuala Iosefo PonifasioPendahuluTuila'epa Sa'ilele MalielegaoiPenggantiPetahanaKetua Fa'atuatua i le Atua Samoa ua TasiPetahanaMulai menjabat 9 Maret 2021WakilLaauli Leuatea PolataivaoPendahuluLaauli Leuatea PolataivaoPenggantiPetahanaDeputi Perdana Menteri SamoaMasa jabatan19 Maret 2016 – 11 ...

El horno ardiente (Toros Roslin, 1266) La Oración de Azarías y el Cántico de los Tres Jóvenes, es un largo pasaje, presente en las biblias Católica y Ortodoxa, y que se ubica después del versículo 23, del capítulo 3 del Libro de Daniel. También se encuentra en la antigua traducción de la Septuaginta. El Artículo IV, de los Treinta y Nueve Artículos de la Iglesia de Inglaterra, lo ha catalogado como no canónico (pero aun así, junto a otros textos apócrifos: La iglesia debe leerl...

American Association of Colleges of NursingLogo of AACNAbbreviationAACNFormation1969Headquarters655 K Street, NW Suite 750 Washington, D.C., United StatesMembership 876 membersBoard ChairJean Giddens, PhD, RNPresident/CEODeborah E. Trautman, PhD, RNWebsitewww.aacnnursing.org The American Association of Colleges of Nursing (AACN) is a national organization of nurses in the United States that is dedicated to advancing nursing education. It was established in 1969, and represents more than 875 m...

1937 Italian filmScipio Africanus: The Defeat of HannibalDirected byCarmine GalloneWritten byCamillo Mariani dell'Aguillara S.A. Luciani Carmine Gallone Silvio MauranoProduced byFederic CuriosiStarringAnnibale Ninchi Camillo Pilotto Isa MirandaProductioncompanyENICRelease date 1937 (1937) Running time83 minutes [1]CountryItalyLanguageItalianBudget12.6 million lira Scipio Africanus: The Defeat of Hannibal[2] (Italian title: Scipione l'africano is a 1937 Italian historical ...

Metro station in Delhi, India Panchsheel Park Delhi Metro stationGeneral informationLocationBlock B, Soami Nagar, New Delhi, 110017Coordinates28°32′32.4161″N 77°13′13.8259″E / 28.542337806°N 77.220507194°E / 28.542337806; 77.220507194Owned byDelhi MetroOperated byDelhi Metro Rail Corporation (DMRC)Line(s)Magenta LinePlatformsIsland platform Platform-1 → Botanical GardenPlatform-2 → Janakpuri WestTracks2ConstructionStructure typeUnderground, Double-track...

Эту страницу предлагается переименовать в «Фернандес-Герра, Аурелиано».Пояснение причин и обсуждение — на странице Википедия:К переименованию/14 мая 2024. Пожалуйста, основывайте свои аргументы на правилах именования статей. Не удаляйте шаблон до подведения итога обсу�...

Spanish politician (born 1965) Marta González VázquezMPFourth Vice President of the Congress of DeputiesIncumbentAssumed office 17 August 2023PresidentFrancina ArmengolPreceded byIgnacio GilDeputy spokesperson of People's Party in the Congress of DeputiesIncumbentAssumed office 3 April 2022PresidentAlberto Núñez FeijóoMember of the Congress of DeputiesIncumbentAssumed office 5 December 2011 Personal detailsBorn (1965-01-25) 25 January 1965 (age 59)Santiago de Compostela,...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 2017 في أستراليامعلومات عامةالسنة 2017 البلد أستراليا 2016 في أستراليا 2018 في أستراليا تعديل - تعديل مصدري - تعد�...






