Bolza surface
|
Read other articles:

Kamen Rider BuildGenreTokusatsuSuperhero fictionScience fictionActionComedy dramaMysteryThrillerConspiracyPembuatShotaro IshinomoriPengembangIshimori ProductionsToei CompanyDitulis olehShogo MutoSutradaraRyuta TasakiKazuya KamihoriuchiSatoshi MorotaShojiro NakazawaKyohei YamaguchiTakayuki ShibasakiPemeranAtsuhiro InukaiEiji AkasoKaho TakadaKouhei TakedaYuki OchiYukari TakiKensei MikamiYasuyuki MaekawaPengisi suaraTetsuo KanaoSora AmamiyaNaratorBucky KobaLagu pembukaBe The One by PANDORA feat...

Divisi Utama Sepak Bola El SalvadorNegara El SalvadorKonfederasiCONCACAFDibentuk1969Jumlah tim12Tingkat pada piramida1Degradasi keSegunda DivisiónPiala ligaCopa El SalvadorPiala internasionalLiga Champions CONCACAFJuara bertahan ligaFASKlub tersuksesFAS (19 gelar)Televisi penyiarCanal 4Tigo SportsSitus webhttps://laprimera.com.sv/ 2022–23 Primera División de El Salvador Primera División dari Liga de Fútbol cuscatleco Profesional (Liga Sepak Bola Profesional), lebih diketahui sebagai La ...

Pour les articles homonymes, voir Basse-Terre (homonymie). Basse-Terre Vue des monts Caraïbes depuis le fort Louis Delgrès à Basse-Terre, la cathédrale Notre-Dame-de-Guadeloupe, le monument aux morts, le fort Delgrès et l'hôtel de ville de Basse-Terre. Blason Administration Pays France Région Guadeloupe Département Guadeloupe(préfecture) Arrondissement Basse-Terre(chef-lieu) Intercommunalité Communauté d'agglomération Grand Sud Caraïbe(siège) Maire Mandat André Atallah (PS) 20...

1976 novel by Kate Wilhelm Where Late the Sweet Birds Sang Cover of first edition (hardcover)AuthorKate WilhelmCover artistM. C. EscherCountryUnited StatesLanguageEnglishGenreScience fiction, dystopianPublisherHarper & RowPublication date1976Media typePrint (hardback & paperback)Pages207AwardsLocus Award for Best Novel (1977)ISBN0-06-014654-0OCLC1529187Dewey Decimal813/.5/4LC ClassPZ4.W678 Wh PS3573.I434 Where Late the Sweet Birds Sang is a science fiction novel by Amer...

Joseph Nicéphore NiépcaNicéphore Niépca, sekitar tahun 1795.Lahir(1765-03-07)7 Maret 1765Chalon-sur-Saône, Saône-et-LoireMeninggal5 Juli 1833(1833-07-05) (umur 68)Saint-Loup-de-Varennes, Saône-et-LoirePekerjaanReka ciptaDikenal atasFotografi'mesin pembakaran internal' pertama di duniaTanda tangan Nicéphore Niépce (lahir Joseph Niépce; 7 Maret 1765 – 5 Juli 1833)[1] adalah seorang penemu asal Prancis, yang sekarang dikenal sebagai penemu fotografi dan sekaligus perint...

James LysterBorn7 September 1810 Died2 September 1891 (aged 80)Alma materTrinity College Dublin Christianity portal James Lyster was an Anglican Dean in the Nineteenth century.[1] Lauder was educated at Trinity College, Dublin He was Dean of Leighlin from 1854 to 1864 [2] when he emigrated to Canada to become Dean of Ontario.[citation needed] He died at Ruthin on 2 September 1891.[3] References ^ Declaring His Genius: Oscar Wilde in North...

First minister for the Canadian province of Nova Scotia Premier of Nova ScotiaPremier ministre de la Nouvelle-ÉcossePrìomhaire Alba NuadhIncumbentTim Houstonsince August 31, 2021Office of the PremierStyle The Honourable (formal) Premier (informal) StatusHead of GovernmentMember ofLegislative AssemblyExecutive CouncilReports toLegislative AssemblyLieutenant GovernorSeatHalifaxAppointerLieutenant Governor of Nova Scotiawith the confidence of the Nova Scotia LegislatureTerm lengthAt His M...

Nymph transformed into hollow water reeds in Greek mythology For other uses, see Syrinx (disambiguation). Pan poursuivant Syrinx drawing by Girodet, 1826 Greek deitiesseries Primordial deities Titans and Olympians Water deities Chthonic deities Personified concepts Nymphs Alseid Anthousai Auloniad Aurae Crinaeae Daphnaie Dryads Eleionomae Epimeliads Hamadryads Hesperides Hyades Lampads Leimakids Leuce Limnades Meliae Melinoë Minthe Naiads Napaeae Nephele Nereids Oceanids Oreads Pegaeae Pegas...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...
The history of emotions is a field of historical research concerned with human emotion, especially variations among cultures and historical periods in the experience and expression of emotions. Beginning in the 20th century with writers such as Lucien Febvre and Peter Gay, an expanding range of methodological approaches is being applied. Scope In the last decade,[which?] the history of emotions has developed into an increasing productive and intellectually stimulating area of histori...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Shin Megami Tensei IV merupakan gim video bermain peran bertema pasca-apokaliptik asal Jepang yang dikembangkan oleh Atlus untuk perangkat Nintendo 3DS. Gim ini merupakan bagian dari seri Shin Megami Tensei, seri utama dari waralaba Megami Tensei, wal...
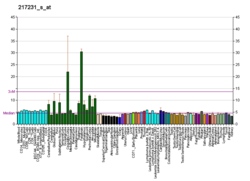
Protein-coding gene in the species Homo sapiens MAST1Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes2M9X, 3PS4IdentifiersAliasesMAST1, SAST, SAST170, microtubule associated serine/threonine kinase 1, MCCCHCMExternal IDsOMIM: 612256 MGI: 1861901 HomoloGene: 10543 GeneCards: MAST1 Gene location (Human)Chr.Chromosome 19 (human)[1]Band19p13.13Start12,833,951 bp[1]End12,874,952 bp[1]Gene location (Mouse)Chr.Chromosome 8 (mouse)[2]Band8 C3|...

Concierge (portiere) in un hotel di Roma. Un portiere[1] o portinaio[2] è un lavoratore che ha il compito di sorvegliare un immobile di natura residenziale, produttiva o terziaria. Indice 1 Compiti 2 Origine del nome 3 Nel mondo 3.1 Italia 3.2 Svizzera 4 Note 5 Bibliografia 6 Filmografia 7 Altri progetti 8 Collegamenti esterni Compiti Il portiere in genere deve accogliere i visitatori dell'immobile e fornire loro le informazioni richieste, ma spesso tra i suoi compiti è comp...

Series of localized seismic events within a short time period Noto earthquake swarm (2020–2024) Chronology of the 2003–2004 Ubaye earthquake swarm Complete caption Each red bar shows the number of earthquakes daily detected (left-handside scale). More than 16,000 earthquakes were detected within 2 years. White circles show the magnitude of ~1,400 earthquakes which could be located (right-handside magnitude scale). Sismalp (the local monitoring network) was not able to locate all events be...

British businessman and Conservative politician, former Deputy Prime Minister of the United Kingdom For the senior civil servant and General Medical Council Registrar, see Michael Heseltine (civil servant). This article may be too long to read and navigate comfortably. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (December 2023) The Right HonourableThe Lord HeseltineCH PCOfficial portrait, 2007Dep...

American actor (born 1979) Jason MomoaMomoa at San Diego Comic-Con in 2018BornJoseph Jason Namakaeha Momoa (1979-08-01) August 1, 1979 (age 44)Honolulu, Hawaii, U.S.Alma materUniversity of Hawaiʻi at MānoaOccupationsActorfilmmakerYears active1999–presentAgentGoldenscreen ManagementSpouse Lisa Bonet (m. 2017; div. 2024)Children2Signature Joseph Jason Namakaeha Momoa (/məˈmoʊə/; born August 1, 1979[1]) is an Amer...

This is a list of parks, historic resources, reserves and recreation areas in the California State Parks system. General location of California's +139 State Parks List of parks Park name Classification County orcounties Size[1] Year established[1] Remarks acres ha Admiral William Standley State Recreation Area State recreation area Mendocino 45 18 1944 Boasts redwoods plus salmon and steelhead fishing on the Eel River.[2] Ahjumawi Lava Springs State Park State park Sh...

明朝关西八卫 赤斤蒙古卫,明朝关西八卫之一,简称赤斤卫,又作赤金卫。 明朝 明朝永乐二年(1404年)元朝丞相苦术之子塔力尼投降明朝,以其所部在赤斤站设置赤斤蒙古千户所,在今甘肃省玉门市西北赤金堡。永乐八年(1410年)升为赤斤卫,正德年间被吐鲁番汗国所破,当地人内徙肃州的南山,赤斤城空。 清朝 清圣祖康熙五十七年(1718年),恢复赤金卫,清世宗雍正...

Tondemo Skill de Isekai Hōrō MeshiSampul novel ringan volume pertamaとんでもスキルで異世界放浪メシ(Tondemo Sukiru de Isekai Hōrō Meshi)GenreKomedi,[1] isekai[1] Seri novelPengarangRen EguchiPenerbitShōsetsuka ni NarōTerbit5 Januari 2016 – sekarang Novel ringanPengarangRen EguchiIlustratorMasaPenerbitOverlapPenerbit bahasa InggrisNA J-Novel ClubImprintOverlap NovelsDemografiPriaTerbit25 November 2016 – sekarangVolume13 MangaPengarangRen EguchiIlustrator...

Shane DawsonShane Dawson pada bulan Juni 2012Informasi pribadiLahirShane Lee Yaw19 Juli 1988 (umur 35)Long Beach, California, Amerika SerikatPekerjaanKomedian, Musisi, dan pembuat filmPasanganRyland Adams (m. 2023)Situs webwww.shanedawsontv.comInformasi YouTubeKanal shane (channel utama) Shane Dawson TV Shane2 Tahun aktif2008–2020, 2021–sekarangGenre vlog comedy kecantikan musik Pelanggan19,4 juta (channel utama)[2]Total tayang4.29 milyar (channel utama)[1]&...

























































