Hilbert manifold
|
Read other articles:

1998 studio album by NileAmongst the Catacombs of Nephren-KaStudio album by NileReleased28 April 1998Recorded1998StudioThe Sound Lab, Columbia, South CarolinaGenreTechnical death metalLength33:07LabelRelapseProducerBob Moore, Earl SandersNile chronology Amongst the Catacombs of Nephren-Ka(1998) Black Seeds of Vengeance(2000) Amongst the Catacombs of Nephren-Ka is the debut studio album by American death metal band Nile. The album was released on April 28, 1998, through Relapse Records...

HaruHaru pada tahun 2018Nama asal波瑠Lahir17 Juni 1991 (umur 32)Adachi, Tokyo, Japan[1]Pekerjaan Aktris model Tahun aktif2004–sekarangAgenHori AgencyTinggi164 cm (5 ft 5 in) Haru (波瑠code: ja is deprecated , Haru, lahir 17 Juni 1991) adalah seorang aktris dan model dari Adachi, Tokyo.[2][3] Sdia dikenal karena film Koizora (2007),[4] Maria-sama ga Miteru (2010),[5] drama televisi bertajuk Asa ga Kita (2015-2016), da...

Judith of BethuliaSutradaraD. W. GriffithDitulis olehThomas Bailey AldrichD. W. GriffithFrank E. WoodsPemeranBlanche SweetHenry B. WalthallSinematograferG. W. BitzerPenyuntingJames SmithPerusahaanproduksiBiograph CompanyDistributorGeneral Film CompanyTanggal rilis 8 Maret 1914 (1914-03-08) Durasi61 menitNegaraAmerika SerikatBahasaFilm bisuIntertitel Inggris Judith of Bethulia Judith of Bethulia (1914) adalah sebuah film Amerika Serikat yang menampilkan Blanche Sweet dan Henry B. Walthall...

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...
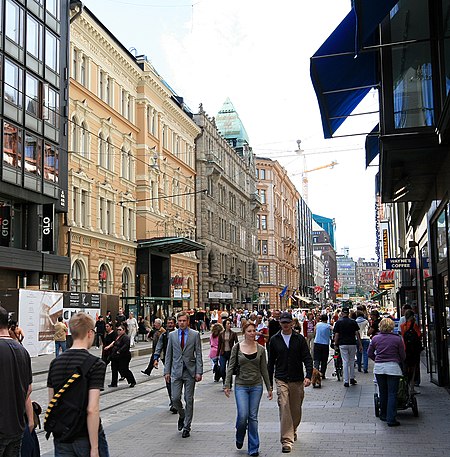
Ekonomi FinlandiaHelsinki, FinlandiaMata uangEuro (EUR)Tahun fiskaltahun kalenderOrganisasi perdaganganEU, WTO dan OECDStatistikPDB$221,539 milyar (2014 PPP)$276.275 milyar (2014 nominal)[1]Pertumbuhan PDB0.2% (Q2 2015 est.) [2]PDB per kapita$40.455(PPP; 2014)[1]PDB per sektorAgrikultur: 2.8%Industri: 25.9%Jasa: 71.2% (2012 est.)Inflasi (IHK) 3.2% (2012 est.)Pendudukdi bawah garis kemiskinan17.9% risiko miskin atau keterasingan sosial[3]Koefisien gini28.2 (2010...

العلاقات الليبية المالطية ليبيا مالطا ليبيا مالطا تعديل مصدري - تعديل العلاقات الليبية المالطية هي العلاقات الثنائية التي تجمع بين ليبيا ومالطا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة ليبيا مالطا �...

2018 American resupply spaceflight to the ISS NG-10Canadarm2 grapples the S.S. John YoungNamesOA-10E (2015–2018)Mission typeISS logisticsOperatorNorthrop GrummanCOSPAR ID2018-092A SATCAT no.43704Mission duration100 days, 4 minutes Spacecraft propertiesSpacecraftS.S. John YoungSpacecraft typeEnhanced Cygnus[1][2]ManufacturerNorthrop GrummanThales Alenia Start of missionLaunch date17 November 2018, 09:01:31 UTCRocketAntares 230[3]Launch siteWallops Pad 0ACont...

Chronologies Le cardinal de Fleury, Premier ministre de Louis XV, donne des nouvelles de Versailles à la reine Marie Leszczynska, alors éloignée de la Cour, et lui annonce entre autres la mort du Prince Eugène. La reine lui répond dans la marge, 30 avril 1736.Données clés 1733 1734 1735 1736 1737 1738 1739Décennies :1700 1710 1720 1730 1740 1750 1760Siècles :XVIe XVIIe XVIIIe XIXe XXeMillénaires :-Ier Ier IIe IIIe Chron...

Cet article est une ébauche concernant une personnalité chinoise et la monarchie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Yu KengFonctionAmbassadeur de Chine en FranceDynastie Qing1899-1902Titre de noblesseLord (en)BiographieDécès 18 décembre 1905ShanghaiNom dans la langue maternelle 裕庚Prénom social 朗西Nationalité chinoiseActivité DiplomateConjoint Louisa Pierson (d)Enfants John Yu Shuinli...

1973 film adaptation by Norman Jewison For the 1970 album, see Jesus Christ Superstar (album). Jesus Christ SuperstarTheatrical release posterDirected byNorman JewisonScreenplay by Melvyn Bragg Norman Jewison Based onJesus Christ Superstarby Andrew Lloyd WebberTim RiceProduced by Norman Jewison Robert Stigwood Starring Ted Neeley Carl Anderson Yvonne Elliman Barry Dennen CinematographyDouglas SlocombeEdited byAntony GibbsMusic byAndrew Lloyd WebberDistributed byUniversal PicturesRelease dates...

English footballer (born 2001) Arthur Okonkwo Okonkwo playing for Sturm Graz in 2023Personal informationFull name Arthur Chukwuezugo Okonkwo[1]Date of birth (2001-09-09) 9 September 2001 (age 22)[2]Place of birth London, EnglandHeight 1.99 m (6 ft 6 in)[3]Position(s) GoalkeeperTeam informationCurrent team Wrexham(on loan from Arsenal)Number 33Youth career Hampstead Academy0000–2009 Lindus Park2009–2021 ArsenalSenior career*Years Team Apps (Gls)2...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

习近平 习近平自2012年出任中共中央总书记成为最高领导人期间,因其废除国家主席任期限制、开启总书记第三任期、集权统治、公共政策与理念、知识水平和自述经历等争议,被中国大陸及其他地区的民众以其争议事件、个人特征及姓名谐音创作负面称呼,用以恶搞、讽刺或批评习近平。对习近平的相关负面称呼在互联网上已经形成了一种活跃、独特的辱包亚文化。 权力�...

伊斯兰合作组织Organisation of Islamic Cooperation(英語)Organisation de la Coopération Islamique(法語)منظمة التعاون الإسلامي(阿拉伯語) 旗帜格言:To safeguard the interests and ensure the progress and well-being of Muslims 成员国 观察国 暂停会籍行政总部 沙地阿拉伯吉达 官方语言阿拉伯语英语法语类型宗教成员国57个在籍成员国(英语:Member states of the Organisation ...

American sports broadcaster (1937–2021) This article is about the American sports broadcaster. For the English footballer, see Joe Tait (footballer). For other people with similar names, see Joseph Tait (disambiguation). Joe TaitTait in 2012Born(1937-05-15)May 15, 1937Evanston, Illinois, U.S.DiedMarch 10, 2021(2021-03-10) (aged 83)Lafayette Township, Ohio, U.S.Sports commentary careerTeam(s)Cleveland CavaliersCleveland IndiansMount Union Purple Raiders Ohio BobcatsIndiana HoosiersGenre...

لمعانٍ أخرى، طالع ري (توضيح). الطرف الثابت لذراع الري المركزي المحوري عند مصدر الري الرّيُّ المعروف أيضًا باسم السقاية، هي الممارسة الزراعية لاستخدام كميات محسوبة من المياه على الأرض للمساعدة في إنتاج المحاصيل. يمكن استخدامه أيضًا في زراعة نباتات المناظر الطبيعية و...

Déclaration unanime des treize États unis d’Amérique Pour un article plus général, voir Déclaration d'indépendance. Déclaration d'indépendance des États-Unis Copie de 1823 de la Déclaration. Titre original The unanimous declaration of the thirteen united States of America (traduction française sur Wikisource) Rédigé le 11 juin au 4 juillet 1776 Présenté le 4 juillet 1776 Ratifié le 4 juillet 1776 Lieu Independence Hall à Philadelphie Commanditaire Secon...

Tiocianato di potassio Nomi alternativisolfocianuro di potassio Caratteristiche generaliFormula bruta o molecolareKSCN Massa molecolare (u)97,18 g/mol Aspettosolido bianco Numero CAS333-20-0 Numero EINECS206-370-1 PubChem516872 SMILESC(#N)[S-].[K+] Proprietà chimico-fisicheDensità (g/cm3, in c.s.)1,89 (20 °C) Solubilità in acqua2170 g/l (20 °C) Temperatura di fusione175 °C (448 K) Temperatura di ebollizione500 °C (773 K) (decomposizione) Indicazioni di sicurezzaSimboli di rischio chimi...

Russian Fencing FederationCategoryFencingJurisdictionRussiaAbbreviationRFF/ФФР/FFRFounded1951/1992AffiliationFédération Internationale d'Escrime (FIE)Regional affiliationEuropean Fencing Confederation (suspended)[1]HeadquartersMoscowPresidentIlgar MamedovChairmanAlisher UsmanovOther key staffYelena Grishina, spokespersonOfficial websitewww.rusfencing.ru The Russian Fencing Federation (RFF; Russian: Федерация Фехтования России (ФФР), romanized: Fe...















