Abstract Wiener space
|
Read other articles:

United States historic placeSeaboard Coast Line Railroad Company Office BuildingU.S. National Register of Historic Places Raleigh and Gaston / Seaboard Coast Line Building at its new 413 North Salisbury Street locationShow map of North CarolinaShow map of the United StatesLocationRaleigh, Wake County, North Carolina, U.S.A.Coordinates35°47′8″N 78°38′25″W / 35.78556°N 78.64028°W / 35.78556; -78.64028Area0.5 acres (0.20 ha)Built1862 (1862)NRHP ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Ekonometrika – berita · surat kabar · buku · cendekiawan · JSTOREkonometrika atau ekonometri (Inggris: econometricscode: en is deprecated , Belanda: econometriecode: nl is deprecated ) adalah ilmu ekonom...

Slovene dialect spoken in southern White Carniola South White Carniolan dialectNative toSloveniaRegionSouthern part of White Carniola, southern from Dobliče and Griblje.EthnicitySlovenesLanguage familyIndo-European Balto-SlavicSlavicSouth SlavicWestern South SlavicSloveneLower Carniolan dialect groupSouth White Carniolan dialectEarly formsSoutheastern Slovene dialect Southern Slovene dialect Lower Carniolan dialect base Dialects Transitional microdialects (northern) Microdialects around...
JariJari tanganJari kakiRincianPengidentifikasiBahasa LatinDigitusDaftar istilah anatomi[sunting di Wikidata] Untuk kota di Brasil, lihat Jari (kota). Jari atau jeriji[1] (Inggris: digit) merupakan bagian ujung dari anggota gerak, seperti tangan dan kaki, yang terdapat pada manusia dan hewan vertebrata. Jari manusia Jari-jari tangan kiri manusia Manusia pada umumnya memiliki 5 buah jari pada setiap ekstremitas yang ada (baik pada tangan maupun kaki), sehingga total jari yang d...

Giosuè Carducci300x300px BiografiKelahiran(it) Giosuè Alessandro Giuseppe Carducci 27 Juli 1835 Valdicastello Carducci (en) Kematian16 Februari 1907 (71 tahun)Bologna Tempat pemakamanCertosa di Bologna (en) Galat: Kedua parameter tahun harus terisi! 44°29′44″N 11°18′35″E / 44.4956629°N 11.3098311°E / 44.4956629; 11.3098311 Senator of the Kingdom of Italy (en) 13 Desember 1890 – Member of the Chamber of Deputies of the Kingdom of Italy (en) 20 Novem...

.org بدأ في 1 يناير 1985؛ منذ 39 سنة (1985-01-01) نوع نطاق المستوى الأعلى العام الحالة Active التسجيل Public Interest Registry (technical service by Afilias) الراعي Not technically sponsored, but PIR is connected with the جمعية الإنترنت الاستخدام المفترض Miscellaneous organizations not fitting in other categories (generally noncommercial) الاستخدام الفعلي Nonprofits; pe...

Érik ComasLahir28 September 1963 (umur 60)Karier Kejuaraan Dunia Formula SatuKebangsaan FrenchTahun aktif1991–1994TimLigier, LarrousseJumlah lomba63 (59 start)Juara Dunia0Menang0Podium0Total poin7Posisi pole0Lap tercepat0Lomba pertamaGrand Prix AS 1991Lomba terakhirGrand Prix Jepang 1994 Érik Comas (lahir 28 September 1963) adalah mantan pembalap Formula 1 dari Prancis. Ia adalah juara F3 Prancis pada tahun 1988, dan kemudian juara Formula 3000 pada tahun 1990, setelah mencetak jumla...

Aircraft used by presidents and prime ministers This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Air transports of heads of state and government – news · newspapers · books · scholar · JSTOR (February 2019) (Learn how and when to remove this template message) Air transports for heads of state and government a...

Taman Nasional Meru BetiriIUCN Kategori II (Taman Nasional)Pemandangan TN Meru BetiriTN Meru BetiriTampilkan peta Kabupaten JemberTN Meru BetiriTampilkan peta BanyuwangiTN Meru BetiriTampilkan peta Provinsi Jawa TimurTN Meru BetiriTampilkan peta JawaTN Meru BetiriTampilkan peta IndonesiaLokasi TN Meru Betiri di Pulau JawaLetakKabupaten Jember dan Kabupaten Banyuwangi, Jawa Timur, IndonesiaKota terdekatJemberLuas58.000 hektare (580 km²)Didirikan1997Pihak pengelolaKementerian Lingkungan Hidup ...

Culinary dish made with a soft flatbread around a filling WrapSmoked chicken and avocado wrapTypeSandwichMain ingredientsFlatbread Media: Wrap A wrap is a culinary dish made with a soft flatbread rolled around a filling. The usual flatbreads are wheat tortillas, lavash, or pita; the filling may include cold sliced meat, poultry, or fish, shredded lettuce, diced tomato or pico de gallo, guacamole, sauteed mushrooms, bacon, grilled onions, cheese, and a sauce, such as ranch or honey m...

Martir-Martir AtlasMeninggal21 Mei 1996 di Tibhirine, AljazairDijadikan martir olehKelompok Islamis Bersenjata atau Angkatan Darat Aljazair reguler[1] Pada malam 26–27 Maret 1996, tujuh rahib dari Biara Atlas di Tibhirine, dekat Médéa, Aljazair, yang berasal dari Ordo Katolik Roma Sistersia (dikenal sebagai Trapis) diculik pada masa Perang Saudara Aljazair. Mereka ditahan selama dua bulan, dan ditemukan tewas pada akhir Mei 1996. Peristiwa penculikan dan kematian mereka masih kont...
28th season of the UEFA club football tournament 1982–83 European CupThe Olympic Stadium in Athens hosted the final.Tournament detailsDates25 August 1982 – 25 May 1983Teams33Final positionsChampions Hamburg (1st title)Runners-up JuventusTournament statisticsMatches played61Goals scored180 (2.95 per match)Attendance1,812,492 (29,713 per match)Top scorer(s)Paolo Rossi (Juventus)6 goals← 1981–82 1983–84 → International football competition The 1982–83 season ...
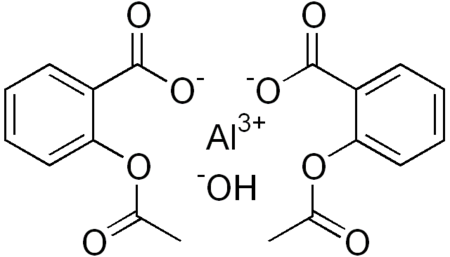
Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Alossiprina Nome IUPACidrossido e 2-acetilossibenzoato di alluminio Caratteristiche generaliFormula bruta o molecolareC18H15AlO9 Massa molecolare (u)402,288 Numero CAS9014-67-9 Numero EINECS245-645-0 Codice ATCB01AC15 PubChem3032790 SMILESCC(=O)OC1=CC=CC=C1C(=O)[O-].CC(=O)OC1=CC=CC=C1C(=O)[O-].[OH-].[Al+3] Ind...

Russian footballer In this name that follows Eastern Slavic naming customs, the patronymic is Inalbekovich and the family name is Mamtov. Khasan Mamtov Mamtov with Tyumen in 2016Personal informationFull name Khasan Inalbekovich MamtovDate of birth (1984-04-28) 28 April 1984 (age 40)Place of birth Besleney, Russian SFSRHeight 1.81 m (5 ft 11 in)Position(s) ForwardSenior career*Years Team Apps (Gls)2002–2003 FC Nart Cherkessk 65 (5)2004–2005 FC Dynamo Stavropol 23 (1...

KNVB beker 1970-1971 Competizione KNVB beker Sport Calcio Edizione 53ª Organizzatore KNVB Luogo Paesi Bassi Cronologia della competizione 1969-70 1971-72 Manuale La KNVB beker 1970-71 fu la 53ª edizione della coppa nazionale di calcio dei Paesi Bassi. Indice 1 Primo turno 2 Secondo turno 3 Ottavi di finale 4 Quarti di finale 5 Semifinali 6 Finale 6.1 Ripetizione 7 Collegamenti esterni Primo turno 15 e 16 agosto 1970. I detentori dell'Ajax E passarono direttamente al turno successivo....

US naval vessel SS Francis J O'Gara on the building ways at J. A. Jones Construction Co. Inc., Panama City, Florida, prior to launching, 8 June 1945. History United States NameFrancis J O'Gara NamesakeFrancis J O'Gara OwnerWar Shipping Administration (WSA) OperatorCalmer Steamship Corp. Orderedas type (EC2-S-C5) hull, MC hull 3140 BuilderJ.A. Jones Construction, Panama City, Florida[1] Laid down14 April 1945 Launched8 June 1945 Completed30 June 1945 Fate Placed in National Defense Res...

馬哈茂德·艾哈迈迪-内贾德محمود احمدینژاد第6任伊朗總統任期2005年8月3日—2013年8月3日副总统帷爾維茲·達烏迪穆罕默德-禮薩·拉希米领袖阿里·哈梅內伊前任穆罕默德·哈塔米继任哈桑·魯哈尼不结盟运动秘书长任期2012年8月30日—2013年8月3日前任穆罕默德·穆尔西继任哈桑·魯哈尼德黑蘭市長任期2003年6月20日—2005年8月3日副职阿里·賽義德盧前任哈桑·馬利克邁達尼�...

Господарський суд Хмельницької областіКраїна УкраїнаВид господарський судІнстанція перша інстанціяЮрисдикція Хмельницька областьЗаснований 1991Суддів 16 + 4 вакантнихГолова Муха Микола ЄвгеновичНа посаді з 21 травня 2020[1]Розташування ХмельницькийАдреса майдан Неза...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

Temple in Daxi, Taoyuan City, Taiwan Furen Temple福仁宮ReligionAffiliationTaoismLocationLocationDaxi, Taoyuan City, TaiwanShown within TaiwanGeographic coordinates24°53′09.9″N 121°17′12.2″E / 24.886083°N 121.286722°E / 24.886083; 121.286722ArchitectureTypetempleDate established1813 The Furen Temple (Chinese: 福仁宮; pinyin: Fúrén Gōng) is a Chinese temple dedicated to Kai Zhang Sheng Wang, and is located along Daxi Old Street in Daxi Distri...







![{\displaystyle [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)
































![{\displaystyle H:=L_{0}^{2,1}([0,T];\mathbb {R} ^{n}):=\{{\text{Absolutely continuous paths starting at 0 with square-integrable first derivative}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c9e9873cc2a6bfba19a5eb797cc71fb2c17690a)
