Complex manifold
|
Read other articles:

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

العلاقات الروسية الجزائرية الجزائر روسيا السفارات سفارة روسيا في الجزائر السفير : ألكسندر زولوتوف العنوان : 7, Chemin du Prince d'Annam, El-Biar, Alger, Algerie سفارة الجزائر في روسيا العنوان : موسكو، كرابيفينسكي بيريولوك، 1А [1] تعديل مصدري - تعديل ...

Serbian politician Nataša MićićНаташа МићићMićić in 2001President of SerbiaActingIn office29 December 2002 – 27 January 2004Prime MinisterZoran ĐinđićZoran ŽivkovićPreceded byMilan MilutinovićSucceeded byDragan Maršićanin (acting)President of the National Assembly of SerbiaIn office6 December 2001 – 27 January 2004Preceded byDragan MaršićaninSucceeded byDragan Maršićanin Personal detailsBorn (1965-11-02) 2 November 1965 (age 58)Titovo Už...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Neo-grotesque sans-serif typeface For the settlement in South Carolina, see Arial, South Carolina. For other uses, see Aerial (disambiguation), Ariel (disambiguation), and Ariaal. ArialCategorySans-serifClassificationNeo-grotesqueDesigner(s) Robin Nicholas Patricia Saunders[1] FoundryMonotype CorporationDate released1982[1]LicenseProprietaryDesign based on Monotype Grotesque Helvetica Venus VariationsArial Unicode MSMetrically compatible with Arimo Liberation Sans Helvetica Ar...

Lambang Provinsi Bengkulu Peta lokasi Provinsi Bengkulu di Indonesia Peta lokasi Kabupaten di Bengkulu Provinsi Bengkulu memiliki 9 kabupaten dan 1 kota dengan ibukota-nya Kota Bengkulu. Berikut daftar kabupaten dan/atau kota di Bengkulu No. Kabupaten/kota Ibu kota Bupati/wali kota luas wilayah (km2)[1] Jumlah penduduk (2022)[1] Kecamatan Kelurahan/desa Lambang Peta lokasi 1 Kabupaten Bengkulu Selatan Kota Manna Gusnan Mulyadi 1.219,22 170.931 11 16/142 2 Kabupaten Bengkulu T...

尤睦佳·泽登巴尔Юмжаагийн Цэдэнбал1970年代时的尤睦佳·泽登巴尔蒙古人民革命党中央委员会总书记任期1958年11月22日—1984年8月24日前任达希·丹巴(第一书记)继任姜巴·巴特蒙赫任期1940年4月8日—1954年4月4日前任达希·丹巴(第一书记)继任达希·丹巴(第一书记)蒙古人民共和國部長會議主席任期1952年1月26日—1974年6月11日前任霍尔洛·乔巴山继任姜巴·巴特蒙赫�...
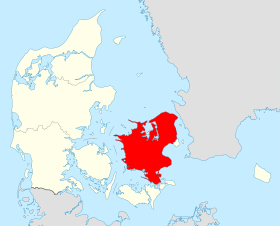
لمعانٍ أخرى، طالع زيلاند (توضيح). زيلاند معلومات جغرافية الإحداثيات 55°34′N 11°53′E / 55.57°N 11.89°E / 55.57; 11.89 [1] [2] الأرخبيل الدنمارك المسطح المائي بحر البلطيق المساحة 7031.30 كيلومتر مربع[3] الطول 132 كيلومتر العرض 116 كيلومتر ال�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅�...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Franz I của Thánh chế La Mãđược vẽ bởi Martin van Meytens, c. 1745Hoàng đế La Mã Thần thánhVua La Mã ĐứcVua ĐứcTại vị13 September 1745 – 18 August 1765Đăng quang4 October 1745, FrankfurtTiền nhiệmKarl VIIKế nhiệmJoseph IIĐại Vương công ÁoTại vị21 November 1740 – 18 August 1765Co-monarchMaria Theresia ITiền nhiệmMaria Theresia IKế nhiệmJoseph IIĐại Công tước xứ ToscanaTại vị12 July 1737 – 18 August 1765Tiền nhi�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 505th Command and Control Wing – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this message) 505th Command and Control Wing Active1947–1952; 1965–1973; 1980–presentCountry United StatesBranch United St...

State highway in Marysville, Washington, U.S. State Route 5284th Street64th StreetSR 528 highlighted in red.Route informationAuxiliary route of I-5Maintained by WSDOTLength3.46 mi[1] (5.57 km)Existed1964[2]–presentMajor junctionsWest end I-5 in MarysvilleMajor intersections SR 529 in MarysvilleEast end SR 9 in Marysville LocationCountryUnited StatesStateWashingtonCountySnohomish Highway system State highways in Washington Interstate US...

American politician and baseball player (1839–1906) For his son, see Arthur Pue Gorman Jr. Senator Gorman redirects here. For other uses, see Senator Gorman (disambiguation). Arthur P. GormanGorman c. 1899Chairman of the Senate Democratic CaucusIn officeMarch 4, 1903 – June 4, 1906Preceded byJames Kimbrough JonesSucceeded byJoseph Clay Stiles BlackburnIn officeMay 3, 1890 – April 1898Preceded byJames B. BeckSucceeded byDavid TurpieUnited States Senatorfrom MarylandIn o...

Racial group Not to be confused with Africans in Turkey. Ethnic group Afro-TurksAfrikalı TürklerTotal populationBetween 5,000 and 20,000[1] [2]Regions with significant populationsMuğla, İzmir, Antalya, Istanbul, Aydın, Denizli, Manisa, Mersin, AdanaLanguagesTurkishReligionIslam Afro-Turks (Turkish: Afrikalı Türkler) are Turkish people of African Zanj descent, who trace their origin to the Ottoman slave trade like the Afro-Abkhazians. Afro-Turk population is estimated to...

Stefan Posch Posch with Austria U21 in 2017Informasi pribadiNama lengkap Stefan PoschTanggal lahir 14 Mei 1997 (umur 27)Tempat lahir Judenburg, AustriaTinggi 188 m (616 ft 10 in)Posisi bermain DefenderInformasi klubKlub saat ini 1899 HoffenheimNomor 38Karier junior Tus Kraubath DSV Leoben Grazer AK AKA HIB Liebenau Sturm Graz0000–2014 Admira Wacker2015–2016 1899 HoffenheimKarier senior*Tahun Tim Tampil (Gol)2014–2015 Admira Wacker Amateure 28 (4)2016– 1899 Hoffenh...

Claudio Caniggia Caniggia bermain untuk Atalanta pada 1999Informasi pribadiNama lengkap Claudio Paul CaniggiaTanggal lahir 9 Januari 1967 (umur 57)Tempat lahir Henderson, Buenos Aires, ArgentinaTinggi 175 m (574 ft 2 in)Posisi bermain Forward / WingerKarier senior*Tahun Tim Tampil (Gol)1985–1988 River Plate 53 (8)1988–1989 Hellas Verona 21 (3)1989–1992 Atalanta 85 (26)1992–1994 Roma 15 (4)1994–1995 Benfica 23 (8)1995–1998 Boca Juniors 74 (32)1999–2000 Atalan...

لمعانٍ أخرى، طالع نادي الصقور (توضيح). نادي الصقور السعودي شعار نادي الصقور السعودي البلد السعودية المقر الرئيسي الرياض تاريخ التأسيس 2017 منطقة الخدمة السعودية الرئيس عبد العزيز بن سعود بن نايف آل سعود الموقع الرسمي موقع النادي الإلكتروني، حسابهم في تويتر تعد�...

Aramaic elaboration of Esther Rabbinic literatureTalmud Readers by Adolf Behrman Talmudic literature Tannaitic Mishnah Tosefta Amoraic (Gemara) Jerusalem Talmud Babylonian Talmud Later Minor Tractates Halakhic Midrash Exodus Mekhilta of Rabbi Ishmael Mekhilta of Rabbi Shimon bar Yochai Leviticus Sifra (Torat Kohanim) Numbers and Deuteronomy Sifre Sifrei Zutta on Numbers (Mekhilta le-Sefer Devarim) Aggadic Midrash Tannaitic Seder Olam Rabbah Alphabet of Rabbi Akiva Baraita of the Forty-nine Ru...



![{\displaystyle N_{J}(X,Y)=[X,Y]+J[JX,Y]+J[X,JY]-[JX,JY]\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0657943fc0c667681387a682be413da0030ec1d)