Embedding
|
Read other articles:

Bagian sebuah scan dari dokumen bersejarah: Judul: Schedelsche Weltchronik atau Kronik Nuremberg Hedwig dari Nordgau (skt. 922 – set. 993) merupakan istri Siegfried dari Luksemburg, Comte dan pendiri negara Luksemburg. Mereka menikah pada sekitar tahun 950.[1] Ia berasal dari Sachsen dan asal usul orangtuanya tidak diketahui secara pasti. Beberapa sumber menyatakan ia adalah putri Comte Eberhard IV dari Nordgau dan Luitgard dari Lotharingia.[2] Yang lainnya menyatakan bahwa ...

Lambang Provinsi Sumatera Barat Peta lokasi Provinsi Sumatera Barat di Indonesia Peta Kabupaten di Sumatera Barat Artikel utama: Daftar kabupaten di Indonesia menurut waktu pembentukan Berikut adalah artikel mengenai Daftar kabupaten dan/atau kota di Sumatera Barat berdasarkan waktu pembentukan yang diurutkan berdasarkan abjad. Referensi berdasarkan Undang-Undang Republik Indonesia yang pertama dikeluarkan saat pembentukan kabupaten/kota tersebut meskipun terdapat perundang-undangan terbaru ...

رودوتوبيون الإحداثيات 39°42′30″N 20°43′36″E / 39.708333333333°N 20.726666666667°E / 39.708333333333; 20.726666666667 تقسيم إداري البلد اليونان[1] عدد السكان عدد السكان 1140 (2011) معلومات أخرى منطقة زمنية ت ع م+02:00 (توقيت قياسي)، وت ع م+03:00 (توقيت صيفي) رمز جيونيمز 254253 تعدي�...

Ketua Dewan Perwakilan Rakyat JepangPetahanaHiroyuki Hosodasejak 10 November 2021Dewan Perwakilan RakyatGelarKetua (informal)Yang Terhormat (formal)Ditunjuk olehDPRMasa jabatanempat tahun; dapat diperbarui hanya jika terjadi pembubaranDasar hukumKonstitusi JepangDibentuk29 November 1890; 133 tahun lalu (1890-11-29)WakilWakil Ketua Dewan Perwakilan Rakyat(衆議院副議長 Shūgiin-fukugichō)Banri Kaieda(sejak 10 November 2021) Ketua Dewan Perwakilan Rakyat (衆議院議長, Shūgi...

Italian football club Football clubGrossetoFull nameSSD Unione Sportiva Grosseto 1912Nickname(s)Il Grifone (The Griffon)Biancorossi (The Red & Whites)Maremmani (The Maremmians)Torelli (The Little Bulls)Unionisti (The Unionists)Founded1912GroundStadio Olimpico Carlo Zecchini,Grosseto, ItalyCapacity10,200OwnerGiovvanni LamioniChairmanAntonio FioriniManagerVitaliano BonuccelliLeagueSerie D Group E3rd Serie D Round Robin EWebsiteClub website Home colours Away colours Third colours Unione Spor...

Kereta api PurwojayaKereta Api Purwojaya liveri spesial hari raya Idulfitri 1444 H berhenti di Stasiun BekasiInformasi umumJenis layananKereta api antarkotaStatusBeroperasiMulai beroperasi13 Maret 1995Operator saat iniKereta Api IndonesiaLintas pelayananStasiun awalCilacapStasiun akhirGambirJarak tempuh404 kmWaktu tempuh rerata6 jam 08 menit[1]Frekuensi perjalananSatu kali keberangkatan tiap hariJenis relRel beratPelayanan penumpangKelasEksekutifPengaturan tempat duduk50 tempat duduk ...

Robert (or Robin) Noble Denison Wilson, known as R. N. D. Wilson (1899 – January 1953)[1] was an Irish poet. From 1934 to 1944 he was a teacher at Rendcomb College.[2] His published work includes the collection The Holy Wells of Orris and other poems (London, John Lane The Bodley Head, 1927),[3] the style of which has been described as early Yeatsian romanticism.[4] Austin Clarke, while agreeing that the book was too much influenced by Yeats, observed th...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

U.S. State Department division This article needs to be updated. The reason given is: more recent employee & budget data needed. Please help update this article to reflect recent events or newly available information. (December 2023) Bureau of East Asian and Pacific AffairsSeal of The Bureau of East Asian and Pacific AffairsBureau overviewPreceding bureauOffice of Chinese AffairsJurisdictionExecutive branch of the United StatesHeadquartersHarry S. Truman Building, Washington, D.C., United...

Pour les articles homonymes, voir Mont-Cenis. Lac du Mont-Cenis Administration Pays France département Savoie commune Val-Cenis Géographie Coordonnées 45° 14′ 16″ N, 6° 56′ 03″ E Type artificiel Montagne Massif du Mont-Cenis Superficie 6,68 km2 Altitude 1 974 m Volume 315 hm3 Hydrographie Bassin versant 295 km2 Émissaire(s) Cenise Géolocalisation sur la carte : France Lac du Mont-Cenis Géolocalisation sur la carte : Rhôn...
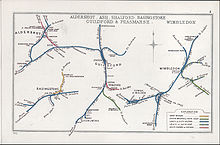
National Rail station in London, England Earlsfield EarlsfieldLocation of Earlsfield in Greater LondonLocationEarlsfieldLocal authorityLondon Borough of WandsworthManaged bySouth Western RailwayStation codeEADDfT categoryDNumber of platforms3 (facing 4 tracks)AccessibleYesFare zone3National Rail annual entry and exit2018–19 6.879 million[1]2019–20 6.519 million[1]2020–21 1.784 million[1]2021–22 4.184 million[1]2022–23 4.734 million[1]Key dates...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

ГеодезіяКоординатна сітка Основи Геодезія Геодинаміка Геоматика Картографія Історія[en] Поняття Географічна відстань Фігура Землі Геоїд • Еліпсоїд Геодезичний датум Геодезична лінія Географічні координати Широта • Довгота Картографічна проєкція Референц-еліпсоїд С...

Wakil Gubernur BantenLambang provinsiPetahanalowongsejak 12 Mei 2022Masa jabatan5 tahunPejabat perdanaRatu Atut ChosiyahDibentuk11 Januari 2002; 22 tahun lalu (2002-01-11)Situs webSitus web resmi Wakil Gubernur Banten merupakan wakil kepala daerah di Banten yang bertugas menjalankan pemerintahan dan membuat kebijakan-kebijakan daerah, seperti membuat peraturan daerah bersama dengan DPRD Provinsi Banten, dan sebagainya. Dalam mengemban tugas-tugas tertentu, seorang wakil gubernur men...

馬里奧·蘇亞雷斯Mário Alberto Nobre Lopes Soares第17任葡萄牙總統任期1986年3月9日—1996年3月9日总理阿尼巴爾·卡瓦科·席爾瓦前任安東尼奧·拉馬爾霍·埃亞內斯继任沈拜奧第114任葡萄牙總理任期1983年6月9日—1985年11月6日前任鮑仕民继任阿尼巴爾·卡瓦科·席爾瓦第107任葡萄牙總理任期1976年7月23日—1978年8月28日前任魏祖承继任阿爾弗雷多·諾布雷·達科斯塔 个人资料出生(1924-12-07)1...

Para otros usos de este término, véase San Miguel. San Miguel del Pino municipio de España Iglesia de San Miguel San Miguel del PinoUbicación de San Miguel del Pino en España San Miguel del PinoUbicación de San Miguel del Pino en la provincia de ValladolidPaís España• Com. autónoma Castilla y León• Provincia Valladolid• Comarca Tierra del Vino• Partido judicial Valladolid[1]Ubicación 41°30′33″N 4°...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Spesialis tanjakan – berita · surat kabar · buku · cendekiawan · JSTOR (December 2013) Marco Pantani adalah seorang spesialis tanjakan Seorang spesialis tanjakan, adalah pembalap sepeda yang dapat berkendara ...

King of Spain from 1886 to 1931 In this Spanish name, the first or paternal surname is Borbón and the second or maternal family name is Habsburgo-Lorena. Alfonso XIIIFormal portrait, 1916King of Spain (more...) Reign17 May 1886 – 14 April 1931 (1886-05-17 – 1931-04-14)Enthronement17 May 1902PredecessorAlfonso XIISuccessorJuan Carlos IRegentMaria Christina (1886–1902)Born(1886-05-17)17 May 1886Royal Palace of Madrid, Madrid, Kingdom of SpainDie...

District of Northern Ireland (1973–2015) Human settlement in Northern IrelandBallymoney BoroughBuirg Bhaile MonaidhBoundaries 1973 to 2015Area418 km2 (161 sq mi) Ranked 17th of 26District HQBallymoneyCatholic31.8%Protestant63.1%CountryNorthern IrelandSovereign stateUnited KingdomCouncillorsMLAsNorth Antrim DUP: 3 Sinn Féin: 1 TUV: 1 UUP: 1MPsIan Paisley Jr. (DUP)Websitewww.ballymoney.gov.uk List of places UK Northern Ireland Ballymoney was a local government distri...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini perlu dirapikan dan ditata ulang agar memenuhi pedoman tata letak Wikipedia. Silakan perbaiki artikel ini agar memenuhi standar Wikipedia. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standa...






































































