Stamnos
|
Read other articles:

This is a list of notable syrups. In cooking, a syrup is a condiment that is a thick, viscous liquid consisting primarily of a solution of sugar in water, containing a large amount of dissolved sugars but showing little tendency to deposit crystals. Its consistency is similar to that of molasses. The viscosity arises from the hydrogen bonds between the dissolved sugar, which has many hydroxyl (OH) groups, and the water. Syrups Cheong A railroad tank car carrying a load of corn syrup Pekmez (...

European records in the sport of athletics are ratified by the European Athletic Association. Records are kept for all events contested at the Olympic Games and some others. Unofficial records for some other events are kept by track and field statisticians. Records are kept for events in track and field, road running, and racewalking. Key to tables Key: Pending ratification Record not kept by European Athletics Not ratified or later rescinded by European A...

Bajrangi Bhaijaan adalah sebuah film drama komedi india tahun 2015 yang disutradarai oleh Kabir Khan. Penulis skenario V. Vijayendra Prasad, film ini diproduksi oleh Salman Khan dan Rockline Venkatesh. Film ini menghadirkan Salman Khan, Harshaali Malhotra, Kareena Kapoor dan Nawazuddin Siddiqui sebagai pemeran utama. Film ini telah dirilis di seluruh dunia pada 17 Juli 2015 saat akhir pekan Idul Fitri. Bajrangi Bhaijaan telah menjadi hit terbesar Salman Khan sampai saat ini, memecahkan rekor...

ليوبليانا علم شعار الاسم الرسمي (بالسلوفينية: Ljubljana)(بالروسية: Лайбах)(بالروسية: Любляна)(بالفرنسية: Laibach) الإحداثيات 46°03′05″N 14°30′22″E / 46.051388888889°N 14.506111111111°E / 46.051388888889; 14.506111111111 تاريخ التأسيس 1144 تقسيم إداري البلد سلوفينيا (25 يوني...
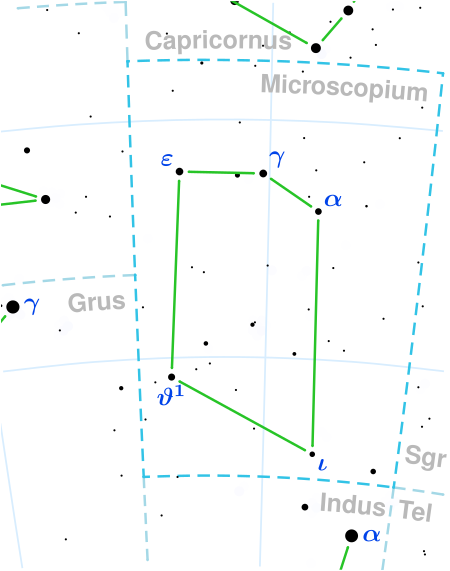
Star in the constellation Microscopium 2 Piscis Austrini Location of 2 PsA (circled) Observation dataEpoch J2000.0 Equinox J2000.0 (ICRS) Constellation Microscopium Right ascension 21h 06m 24.67730s[1] Declination −32° 20′ 29.8282″[1] Apparent magnitude (V) 5.20±0.01[2] Characteristics Evolutionary stage horizontal branch[3] Spectral type K2 III[4] or K3 III[5] ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

American politician This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this message) Thomas L. OwensFrontispiece of 1950's Thomas Leonard Owens, Late a RepresentativeMember of the U.S. House of Representativesfrom Illinois's 7th districtIn officeJanuary 3, 1947 – ...

Williams nel 2017 Mark Williams (Bromsgrove, 22 agosto 1959) è un attore, comico e sceneggiatore britannico. È noto principalmente per aver interpretato Arthur Weasley nei film tratti dalla saga di Harry Potter e l'omonimo protagonista nella serie TV della BBC Padre Brown. Indice 1 Biografia 2 Filmografia parziale 2.1 Cinema 2.2 Televisione 3 Doppiatore 4 Doppiatori italiani 5 Altri progetti 6 Collegamenti esterni Biografia Dal pubblico britannico è conosciuto principalmente come uno dei p...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

German footballer (born 1994) You can help expand this article with text translated from the corresponding article in German. (February 2022) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translat...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) جمعية طلبة شمال أفريقيا المسلمين هي جمعية تأسست في باريس في كانون الأول 1927، على يد طلبة تونسيون وجزائريو�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Muhammad Syafiuddin II Muhammad Syafiuddin II (18 November 1841 – 12 September 1924) adalah seorang sultan Sambas. Pada 1891, ia dianugerahi Bahaderi Singa Nederland (Rider in de orde van den Nederlansche Indie Leeuw) oleh Raja William...

16-Ketoestrone Names IUPAC name 3-Hydroxyestra-1,3,5(10)-triene-16,17-dione Systematic IUPAC name (3aS,3bR,9bS,11aS)-7-Hydroxy-11a-methyl-3a,3b,4,5,9b,10,11,11a-octahydro-1H-cyclopenta[a]phenanthrene-1,2(3H)-dione Other names 16-Oxoestrone; 16-Keto-E1; 16-Oxo-E1; NSC-60462 Identifiers CAS Number 1228-73-5 3D model (JSmol) Interactive image ChEBI CHEBI:34166 ChemSpider 216072 KEGG C14441 PubChem CID 246876 UNII 113V416QTU CompTox Dashboard (EPA) DTXSID701261036 InChI InChI=1S/C18H20O3/c1-18-7...
American politician and 31st Governor of Wisconsin Orland LoomisGovernor-elect of WisconsinDied before assuming officePreceded byJulius P. HeilSucceeded byWalter Samuel Goodland28th Attorney General of WisconsinIn officeJanuary 4, 1937 – January 2, 1939GovernorPhilip La FollettePreceded byJames E. FinneganSucceeded byJohn E. MartinMember of the Wisconsin Senatefrom the 31st districtIn officeJanuary 5, 1931 – January 7, 1935Preceded byHoward TeasdaleSucceeded byJames Earl...

6th round of the 2017 Formula One season Monaco Grand Prix 75 redirects here. For the race run in 1975, see 1975 Monaco Grand Prix. 2017 Monaco Grand Prix Race 6 of 20 in the 2017 Formula One World Championship← Previous raceNext race → Layout of the Circuit de Monte Carlo, MonacoRace detailsDate 28 May 2017Official name 75e Formula 1 Grand Prix de Monaco[1][2]Location Circuit de MonacoLa Condamine and Monte Carlo, MonacoCourse Street circuitCourse leng...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2009) (Learn how and when to remove this message) The Drunkard's Progress: A lithograph by Nathaniel Currier supporting the temperance movement, January 1846. The Methodist Episcopal Church Board of Temperance, Prohibition, and Public Morals was a major organization i...

Welsh astrophysicist (b1969) This article is about the astrophysicist. For the former Wales international rugby union player, see Geraint Lewis. A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (September 2021) (Learn how and when to remove this message) Geraint Francis LewisLewis at the Sydney Institute for As...

Punitive practice This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The examples and perspective in this article may not include all significant viewpoints. Please improve the article or discuss the issue. (August 2012) (Learn how and when to remove this message) This article's factual accuracy may be compromised due to out-of-date information. Please help update this article to reflect rec...

Pour les articles homonymes, voir Derby. Cet article est une ébauche concernant l’Angleterre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mai 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abor...

This article is about matrices whose entries are integer numbers. For use of term unimodular in connection with polynomial matrices, see Unimodular polynomial matrix. Integer matrices with +1 or -1 determinant; invertible over the integers. GL_n(Z) In mathematics, a unimodular matrix M is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N that is its inverse (these are equivalent under...

