Empty set
|
Read other articles:

Finding FannyPoster rilis teatrikalSutradaraHomi AdajaniaProduserDinesh VijanDitulis olehHomi AdajaniaSuvidesh ShingadePemeranNaseeruddin ShahDimple KapadiaPankaj KapurDeepika PadukoneArjun KapoorNaratorDeepika PadukonePenata musikMathias DuplessySachin-JigarSinematograferAnil MehtaPenyuntingSreekar Prasad (India- Inggris dan Hindi)Nick Moore (Internasional- Inggris)PerusahaanproduksiMaddock FilmsDistributorFox Star StudiosTanggal rilis 12 September 2014 (2014-09-12) Durasi101 meni...

1977 film by Robert Aldrich The ChoirboysDirected byRobert AldrichWritten byJennifer MillerProduced byMerv AdelsonLee RichStarring Charles Durning Louis Gossett Jr. Perry King Clyde Kusatsu Stephen Macht Tim McIntire Randy Quaid Chuck Sacci Don Stroud James Woods Burt Young CinematographyJoseph BirocEdited byWilliam MartinIrving RosenblumMaury WinetrobeMusic byFrank De VolProductioncompanyLorimar ProductionsDistributed byUniversal PicturesRelease date December 23, 1977 (1977-12...

PlayStation 3Original PlayStation 3 logo (2006–2009)Revised PlayStation 3 logo (2009–2017) Atas: PlayStation 3 asli (2006) Tengah: PlayStation 3 Slim (2009) Bawah: PlayStation 3 Super Slim (2012) PengembangSony Interactive EntertainmentPembuatSony, Foxconn, Asus[1]Keluarga produkPlayStationJenisKonsol permainan video rumahGenerasiKetujuhTanggal rilisJP: 11 November 2006; 17 tahun lalu (2006-11-11)NA: 17 November 2006; 17 tahun lalu (2006-11-17)PAL: 23 Maret 2007; 17 tah...

For other people with the same name, see Alan Lee (disambiguation). Illustrator and movie conceptual designer Alan LeeLee in 2016Born (1947-08-20) 20 August 1947 (age 76)Middlesex, EnglandEducationEaling School of ArtKnown forIllustration, painting, conceptual designAwardsChesley Award 1989, 1998 Kate Greenaway Medal 1993 World Fantasy Award 1998 Academy Award 2004 Signature Alan Lee (born 20 August 1947) is an English book illustrator and film conceptual designer. He is best known ...

Aldo De BenedettiLahir(1892-08-13)13 Agustus 1892Roma, ItaliaMeninggal19 Januari 1970(1970-01-19) (umur 77)Roma, ItaliaPekerjaanPenulis naskahTahun aktif1920-1958 Aldo De Benedetti (13 Agustus 1892 – 19 Januari 1970) adalah seorang penulis naskah asal Italia. Ia menulis untuk 118 film antara 1920 dan 1958. Ia lahir dan meninggal di Roma, Italia.[1] Filmografi pilihan Marco Visconti (1925) What Scoundrels Men Are! (1932) Mr. Desire (1934) Just Married (1934) ...

Racine antérieure du nerf spinal1 - Neurones sensitifs 2 - Neurones moteurs 3 - Moelle spinale 4 - Substance blanche 5 - Substance grise 6 - Racine antérieure ou motrice 7 - Racine postérieure ou sensitive 8 - Ganglion spinal 9 - Nerf spinal 10 - Rameau postérieur ou dorsal 11 - Rameau antérieur ou ventral 12 - Rameaux communicants 13 - Rameau communicant gris 14 - Rameau communicant blanc 15 - Tronc sympathique latérovertébral 16 - rameau interganglionnaire du tronc sympathique 17 - G...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Diskografi (G)I-dle(G)I-dle membawakan Tomboy di Warfield Theatre di San Francisco, California pada 24 Juli 2022.Video musik10Extended play6Singel8Album soundtrack2Other songs2Collaborations7Single albums1 Girl group Korea Selatan (G)I-dle telah merilis enam extended play, satu album singel dan delapan singel digital. Mereka juga telah berpartisipasi dalam enam lagu kolaborasi, dua kontribusi soundtrack dan dua belas video musik. Dibentuk oleh Cube Entertainment pada tahun 2018, (G)I-dle debu...

Halaman ini berisi artikel tentang unsur kimia. Untuk kegunaan lain, lihat Plutonium (disambiguasi). Artikel ini bukan mengenai Polonium. 94PuPlutoniumSampel plutonium berdiameter ~44 mm Garis spektrum plutoniumSifat umumNama, lambangplutonium, PuPengucapan/plutonium/[1] Alotroplihat alotrop plutoniumPenampilanputih keperakan, teroksidasi menjadi abu-abu gelap ketika terpapar dengan udaraPlutonium dalam tabel periodik 94Pu Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Ok...

Voce principale: Olympique Lyonnais. Olympique LyonnaisStagione 2004-2005Sport calcio Squadra Olympique Lione Allenatore Paul Le Guen Presidente Jean-Michel Aulas Ligue 11º (in Champions League) Coppa di FranciaOttavi di finale Coupe de la LigueSedicesimi di finale Champions LeagueQuarti di finale Maggiori presenzeCampionato: Essien, Malouda (37) Miglior marcatoreCampionato: Juninho (13) StadioGerland (43 051) 2003-2004 2005-2006 Si invita a seguire il modello di voce Questa voce ...

Political party in France Convention of Republican Institutions Convention des institutions républicainesAbbreviationCIRLeaderFrançois MitterrandFoundedJune 1964Dissolved1971Merged intoSocialist PartyIdeologySocialismRepublicanismNational affiliationFGDSPolitics of FrancePolitical partiesElections The Convention of Republican Institutions (French: Convention des institutions républicaines, CIR) was a socialist and republican party in France led by François Mitterrand. The CIR, fo...

Convention center in Chicago (demolished) The Wigwam - 1860 Republican National Convention The Wigwam was a convention center and meeting hall that served as the site of the 1860 Republican National Convention.[1] It was located in Chicago, Illinois, at Lake Street and Market (later Wacker Drive) near the Chicago River.[2] This site had previously been the site of the Sauganash Hotel, Chicago's first hotel.[1] This is where supporters ushered Abraham Lincoln to the par...

British doctor Francis GlissonFrancis GlissonBorn1597Bristol, EnglandDied14 October 1677London, EnglandNationalityBritishKnown forFibrous capsule of GlissonScientific careerFieldsPhysician Francis Glisson (1597[1] – 14 October 1677[2]) was a British physician, anatomist, and writer on medical subjects. He did important work on the anatomy of the liver, and he wrote an early pediatric text on rickets. An experiment he performed helped debunk the balloonist theory of ...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Песня и танецSong and Dance Музыка Эндрю Ллойд Уэббер Слова Дон Блэк Ричард Молтби-мл. Награды Tony Award for Best Actress in a Musical (Питерс, победительница)Drama Desk Award for Outstanding Actress in a Musical (Питерс, победительница) Язык английский Постановки 1982 Вест-Энд 1983 Австралия1985 Бродвей2007 Израиль «Песня и т...

Constitutional body of the Congress of the Philippines For the Indian government committee, see Appointments Committee of the Cabinet. Commission on Appointments19th CongressHistoryFounded1935 (1935)1987 (1987) (reestablishment)New session startedJuly 25, 2022 (2022-07-25)LeadershipChairmanFrancis Escudero, NPC since May 20, 2024 Vice ChairmanRamon Guico Jr., Lakas since August 23, 2022 Majority LeaderLuis Raymund Villafuerte, NUP since August 23, 2022 Min...

Canadian-American polymath (1835–1909) For the Australian rower, see Simon Newcomb (rower). Simon NewcombNewcomb c. 1905Born(1835-03-12)March 12, 1835Wallace, Nova Scotia, CanadaDiedJuly 11, 1909(1909-07-11) (aged 74)Washington, D.C., U.S.NationalityCanadianCitizenshipAmericanAlma materHarvard University (BS, 1858)Spouse Mary Caroline Hassler (m. 1863)Children4, incl. Anita Newcomb McGee and Anna Josepha also William Bartlett Newcomb and Emil...

† Большая гавайская древесница Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:За...
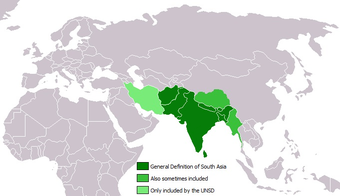
Subregion in Asia This article is about the geographical subregion of Asia. For the physiographical region of Eurasia, see Indian subcontinent.Not to be confused with Southern Asia (UN geoscheme). South AsiaArea5,222,321 km2 (2,016,349 sq mi)Population2.04 billion (2024)[1]Population density362.3/km2 (938/sq mi)GDP (PPP)$18.05 trillion (2024)[2]GDP (nominal)$5.04 trillion (2024)[3]GDP per capita$2,650 (nominal) (2024)$9,470 (PPP) (202...

Archaeological site in Florida, United States This article lacks inline citations besides NRIS, a database which provides minimal and sometimes ambiguous information. Please help ensure the accuracy of the information in this article by providing inline citations to additional reliable sources. (November 2013) (Learn how and when to remove this message) United States historic placePorter's Bar SiteU.S. National Register of Historic Places Show map of FloridaShow map of the United StatesLocati...