Cantor's diagonal argument (among various similar names^{[note 1]}) is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers – informally, that there are sets which in some sense contain more elements than there are positive integers. Such sets are now called uncountable sets, and the size of infinite sets is treated by the theory of cardinal numbers, which Cantor began.

Georg Cantor published this proof in 1891,^{[1][2]: 20– [3]} but it was not his first proof of the uncountability of the real numbers, which appeared in 1874.^[4][5] However, it demonstrates a general technique that has since been used in a wide range of proofs,^[6] including the first of Gödel's incompleteness theorems^[2] and Turing's answer to the Entscheidungsproblem. Diagonalization arguments are often also the source of contradictions like Russell's paradox^[7][8] and Richard's paradox.^[2]: 27

Uncountable set

Cantor considered the set T of all infinite sequences of binary digits (i.e. each digit is zero or one).^{[note 2]} He begins with a constructive proof of the following lemma:

If s₁, s₂, ... , s_n, ... is any enumeration of elements from T,^{[note 3]} then an element s of T can be constructed that doesn't correspond to any s_n in the enumeration.

The proof starts with an enumeration of elements from T, for example

s1 =	(0,	0,	0,	0,	0,	0,	0,	...)
s2 =	(1,	1,	1,	1,	1,	1,	1,	...)
s3 =	(0,	1,	0,	1,	0,	1,	0,	...)
s4 =	(1,	0,	1,	0,	1,	0,	1,	...)
s5 =	(1,	1,	0,	1,	0,	1,	1,	...)
s6 =	(0,	0,	1,	1,	0,	1,	1,	...)
s7 =	(1,	0,	0,	0,	1,	0,	0,	...)
...

Next, a sequence s is constructed by choosing the 1st digit as complementary to the 1st digit of s₁ (swapping 0s for 1s and vice versa), the 2nd digit as complementary to the 2nd digit of s₂, the 3rd digit as complementary to the 3rd digit of s₃, and generally for every n, the n^th digit as complementary to the n^th digit of s_n. For the example above, this yields

s1	=	(0,	0,	0,	0,	0,	0,	0,	...)
s2	=	(1,	1,	1,	1,	1,	1,	1,	...)
s3	=	(0,	1,	0,	1,	0,	1,	0,	...)
s4	=	(1,	0,	1,	0,	1,	0,	1,	...)
s5	=	(1,	1,	0,	1,	0,	1,	1,	...)
s6	=	(0,	0,	1,	1,	0,	1,	1,	...)
s7	=	(1,	0,	0,	0,	1,	0,	0,	...)
...
s	=	(1,	0,	1,	1,	1,	0,	1,	...)

By construction, s is a member of T that differs from each s_n, since their n^th digits differ (highlighted in the example). Hence, s cannot occur in the enumeration.

Based on this lemma, Cantor then uses a proof by contradiction to show that:

The set T is uncountable.

The proof starts by assuming that T is countable. Then all its elements can be written in an enumeration s₁, s₂, ... , s_n, ... . Applying the previous lemma to this enumeration produces a sequence s that is a member of T, but is not in the enumeration. However, if T is enumerated, then every member of T, including this s, is in the enumeration. This contradiction implies that the original assumption is false. Therefore, T is uncountable.^[1]

Real numbers

The uncountability of the real numbers was already established by Cantor's first uncountability proof, but it also follows from the above result. To prove this, an injection will be constructed from the set T of infinite binary strings to the set R of real numbers. Since T is uncountable, the image of this function, which is a subset of R, is uncountable. Therefore, R is uncountable. Also, by using a method of construction devised by Cantor, a bijection will be constructed between T and R. Therefore, T and R have the same cardinality, which is called the "cardinality of the continuum" and is usually denoted by ${\displaystyle {\mathfrak {c}}}$ or ${\displaystyle 2^{\aleph _{0}}}$.

An injection from T to R is given by mapping binary strings in T to decimal fractions, such as mapping t = 0111... to the decimal 0.0111.... This function, defined by f (t) = 0.t, is an injection because it maps different strings to different numbers.^{[note 4]}

Constructing a bijection between T and R is slightly more complicated. Instead of mapping 0111... to the decimal 0.0111..., it can be mapped to the base b number: 0.0111..._b. This leads to the family of functions: f_b (t) = 0.t_b. The functions f _b(t) are injections, except for f ₂(t). This function will be modified to produce a bijection between T and R.

Construction of a bijection between T and R

The function h: (0,1) → (−π/2,π/2) The function tan: (−π/2,π/2) → R This construction uses a method devised by Cantor that was published in 1878. He used it to construct a bijection between the closed interval [0, 1] and the irrationals in the open interval (0, 1). He first removed a countably infinite subset from each of these sets so that there is a bijection between the remaining uncountable sets. Since there is a bijection between the countably infinite subsets that have been removed, combining the two bijections produces a bijection between the original sets.[9] Cantor's method can be used to modify the function f 2(t) = 0.t2 to produce a bijection from T to (0, 1). Because some numbers have two binary expansions, f 2(t) is not even injective. For example, f 2(1000...) = 0.1000...2 = 1/2 and f 2(0111...) = 0.0111...2 = 1/4 + 1/8 + 1/16 + ... = 1/2, so both 1000... and 0111... map to the same number, 1/2. To modify f2 (t), observe that it is a bijection except for a countably infinite subset of (0, 1) and a countably infinite subset of T. It is not a bijection for the numbers in (0, 1) that have two binary expansions. These are called dyadic numbers and have the form m / 2n where m is an odd integer and n is a natural number. Put these numbers in the sequence: r = (1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8, ...). Also, f2 (t) is not a bijection to (0, 1) for the strings in T appearing after the binary point in the binary expansions of 0, 1, and the numbers in sequence r. Put these eventually-constant strings in the sequence: s = (000..., 111..., 1000..., 0111..., 01000..., 00111..., 11000..., 10111..., ...). Define the bijection g(t) from T to (0, 1): If t is the nth string in sequence s, let g(t) be the nth number in sequence r ; otherwise, g(t) = 0.t2. To construct a bijection from T to R, start with the tangent function tan(x), which is a bijection from (−π/2, π/2) to R (see the figure shown on the right). Next observe that the linear function h(x) = πx – π/2 is a bijection from (0, 1) to (−π/2, π/2) (see the figure shown on the left). The composite function tan(h(x)) = tan(πx – π/2) is a bijection from (0, 1) to R. Composing this function with g(t) produces the function tan(h(g(t))) = tan(πg(t) – π/2), which is a bijection from T to R.

General sets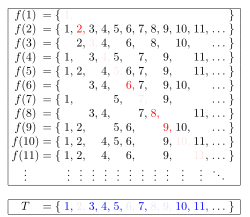

A generalized form of the diagonal argument was used by Cantor to prove Cantor's theorem: for every set S, the power set of S—that is, the set of all subsets of S (here written as P(S))—cannot be in bijection with S itself. This proof proceeds as follows:

Let f be any function from S to P(S). It suffices to prove f cannot be surjective. That means that some member T of P(S), i.e. some subset of S, is not in the image of f. As a candidate consider the set:

T = { s ∈ S: s ∉ f(s) }.

For every s in S, either s is in T or not. If s is in T, then by definition of T, s is not in f(s), so T is not equal to f(s). On the other hand, if s is not in T, then by definition of T, s is in f(s), so again T is not equal to f(s); cf. picture. For a more complete account of this proof, see Cantor's theorem.

Consequences

Ordering of cardinals

With equality defined as the existence of a bijection between their underlying sets, Cantor also defines binary predicate of cardinalities ${\displaystyle |S|}$ and ${\displaystyle |T|}$ in terms of the existence of injections between ${\displaystyle S}$ and ${\displaystyle T}$. It has the properties of a preorder and is here written "${\displaystyle \leq }$". One can embed the naturals into the binary sequences, thus proving various injection existence statements explicitly, so that in this sense ${\displaystyle |{\mathbb {N} }|\leq |2^{\mathbb {N} }|}$, where ${\displaystyle 2^{\mathbb {N} }}$ denotes the function space ${\displaystyle {\mathbb {N} }\to \{0,1\}}$. But following from the argument in the previous sections, there is no surjection and so also no bijection, i.e. the set is uncountable. For this one may write ${\displaystyle |{\mathbb {N} }|<|2^{\mathbb {N} }|}$, where "${\displaystyle <}$" is understood to mean the existence of an injection together with the proven absence of a bijection (as opposed to alternatives such as the negation of Cantor's preorder, or a definition in terms of assigned ordinals). Also ${\displaystyle |S|<|{\mathcal {P}}(S)|}$ in this sense, as has been shown, and at the same time it is the case that ${\displaystyle \neg (|{\mathcal {P}}(S)|\leq |S|)}$, for all sets ${\displaystyle S}$.

Assuming the law of excluded middle, characteristic functions surject onto powersets, and then ${\displaystyle |2^{S}|=|{\mathcal {P}}(S)|}$. So the uncountable ${\displaystyle 2^{\mathbb {N} }}$ is also not enumerable and it can also be mapped onto ${\displaystyle {\mathbb {N} }}$. Classically, the Schröder–Bernstein theorem is valid and says that any two sets which are in the injective image of one another are in bijection as well. Here, every unbounded subset of ${\displaystyle {\mathbb {N} }}$ is then in bijection with ${\displaystyle {\mathbb {N} }}$ itself, and every subcountable set (a property in terms of surjections) is then already countable, i.e. in the surjective image of ${\displaystyle {\mathbb {N} }}$. In this context the possibilities are then exhausted, making "${\displaystyle \leq }$" a non-strict partial order, or even a total order when assuming choice. The diagonal argument thus establishes that, although both sets under consideration are infinite, there are actually more infinite sequences of ones and zeros than there are natural numbers. Cantor's result then also implies that the notion of the set of all sets is inconsistent: If ${\displaystyle S}$ were the set of all sets, then ${\displaystyle {\mathcal {P}}(S)}$ would at the same time be bigger than ${\displaystyle S}$ and a subset of ${\displaystyle S}$.

In the absence of excluded middle

Also in constructive mathematics, there is no surjection from the full domain ${\displaystyle {\mathbb {N} }}$ onto the space of functions ${\displaystyle {\mathbb {N} }^{\mathbb {N} }}$ or onto the collection of subsets ${\displaystyle {\mathcal {P}}({\mathbb {N} })}$, which is to say these two collections are uncountable. Again using "${\displaystyle <}$" for proven injection existence in conjunction with bijection absence, one has ${\displaystyle {\mathbb {N} }<2^{\mathbb {N} }}$ and ${\displaystyle S<{\mathcal {P}}(S)}$. Further, ${\displaystyle \neg ({\mathcal {P}}(S)\leq S)}$, as previously noted. Likewise, ${\displaystyle 2^{\mathbb {N} }\leq {\mathbb {N} }^{\mathbb {N} }}$, ${\displaystyle 2^{S}\leq {\mathcal {P}}(S)}$ and of course ${\displaystyle S\leq S}$, also in constructive set theory.

It is however harder or impossible to order ordinals and also cardinals, constructively. For example, the Schröder–Bernstein theorem requires the law of excluded middle.^[10] In fact, the standard ordering on the reals, extending the ordering of the rational numbers, is not necessarily decidable either. Neither are most properties of interesting classes of functions decidable, by Rice's theorem, i.e. the set of counting numbers for the subcountable sets may not be recursive and can thus fail to be countable. The elaborate collection of subsets of a set is constructively not exchangeable with the collection of its characteristic functions. In an otherwise constructive context (in which the law of excluded middle is not taken as axiom), it is consistent to adopt non-classical axioms that contradict consequences of the law of excluded middle. Uncountable sets such as ${\displaystyle 2^{\mathbb {N} }}$ or ${\displaystyle {\mathbb {N} }^{\mathbb {N} }}$ may be asserted to be subcountable.^[11][12] This is a notion of size that is redundant in the classical context, but otherwise need not imply countability. The existence of injections from the uncountable ${\displaystyle 2^{\mathbb {N} }}$ or ${\displaystyle {\mathbb {N} }^{\mathbb {N} }}$ into ${\displaystyle {\mathbb {N} }}$ is here possible as well.^[13] So the cardinal relation fails to be antisymmetric. Consequently, also in the presence of function space sets that are even classically uncountable, intuitionists do not accept this relation to constitute a hierarchy of transfinite sizes.^[14] When the axiom of powerset is not adopted, in a constructive framework even the subcountability of all sets is then consistent. That all said, in common set theories, the non-existence of a set of all sets also already follows from Predicative Separation.

In a set theory, theories of mathematics are modeled. Weaker logical axioms mean fewer constraints and so allow for a richer class of models. A set may be identified as a model of the field of real numbers when it fulfills some axioms of real numbers or a constructive rephrasing thereof. Various models have been studied, such as the Cauchy reals or the Dedekind reals, among others. The former relate to quotients of sequences while the later are well-behaved cuts taken from a powerset, if they exist. In the presence of excluded middle, those are all isomorphic and uncountable. Otherwise, variants of the Dedekind reals can be countable^[15] or inject into the naturals, but not jointly. When assuming countable choice, constructive Cauchy reals even without an explicit modulus of convergence are then Cauchy-complete^[16] and Dedekind reals simplify so as to become isomorphic to them. Indeed, here choice also aids diagonal constructions and when assuming it, Cauchy-complete models of the reals are uncountable.

Open questions

Motivated by the insight that the set of real numbers is "bigger" than the set of natural numbers, one is led to ask if there is a set whose cardinality is "between" that of the integers and that of the reals. This question leads to the famous continuum hypothesis. Similarly, the question of whether there exists a set whose cardinality is between |S| and |P(S)| for some infinite S leads to the generalized continuum hypothesis.

Diagonalization in broader context

Russell's paradox has shown that set theory that includes an unrestricted comprehension scheme is contradictory. Note that there is a similarity between the construction of T and the set in Russell's paradox. Therefore, depending on how we modify the axiom scheme of comprehension in order to avoid Russell's paradox, arguments such as the non-existence of a set of all sets may or may not remain valid.

Analogues of the diagonal argument are widely used in mathematics to prove the existence or nonexistence of certain objects. For example, the conventional proof of the unsolvability of the halting problem is essentially a diagonal argument. Also, diagonalization was originally used to show the existence of arbitrarily hard complexity classes and played a key role in early attempts to prove P does not equal NP.

Version for Quine's New Foundations

The above proof fails for W. V. Quine's "New Foundations" set theory (NF). In NF, the naive axiom scheme of comprehension is modified to avoid the paradoxes by introducing a kind of "local" type theory. In this axiom scheme,

{ s ∈ S: s ∉ f(s) }

is not a set — i.e., does not satisfy the axiom scheme. On the other hand, we might try to create a modified diagonal argument by noticing that

{ s ∈ S: s ∉ f({s}) }

is a set in NF. In which case, if P₁(S) is the set of one-element subsets of S and f is a proposed bijection from P₁(S) to P(S), one is able to use proof by contradiction to prove that |P₁(S)| < |P(S)|.

The proof follows by the fact that if f were indeed a map onto P(S), then we could find r in S, such that f({r}) coincides with the modified diagonal set, above. We would conclude that if r is not in f({r}), then r is in f({r}) and vice versa.

It is not possible to put P₁(S) in a one-to-one relation with S, as the two have different types, and so any function so defined would violate the typing rules for the comprehension scheme.

See also

• Cantor's first uncountability proof
• Controversy over Cantor's theory
• Diagonal lemma

Notes

References

External links

• Cantor's Diagonal Proof at MathPages
• Weisstein, Eric W. "Cantor Diagonal Method". MathWorld.