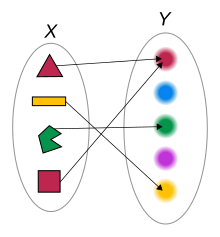
Map (mathematics)
|
Read other articles:

Stefani StoevaInformasi pribadiNama lahirStefani StoevaKebangsaan BulgariaLahir23 September 1995 (umur 28)[1]Galabovo, Bulgaria[1]Tinggi173 m (567 ft 7 in)Tahun aktif2009PeganganKananGanda putriPeringkat tertinggi8 (8 November 2018)Peringkat saat ini10 bersama Gabriela Stoeva (8 November 2022[2])Profil di BWF Stefani Stoeva (bahasa Bulgaria: Стефани Стоева; lahir 23 September 1995) adalah pemain bulu tangkis putri ber...

1 Samuel 31Kitab Samuel (Kitab 1 & 2 Samuel) lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab 1 SamuelKategoriNevi'imBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen9← pasal 30 2 Samuel 1 → 1 Samuel 31 (atau I Samuel 31, disingkat 1Sam 31) adalah bagian terakhir dari Kitab 1 Samuel dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Dalam Alkitab Ibrani termasuk Nabi-nabi Awal atau Nevi'im Rishonim [נביאים ראשונים] dalam bagian Ne...

Katedral GradoKatedral-Basilika Santa EufemiaItalia: Basilica di S. Eufemiacode: it is deprecated Katedral GradoLokasiGradoNegaraItaliaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Agung Gorizia Katedral Grado yang bernama resmi Basilika Santa Eufemia (Italia: Basilica di Sant'Eufemiacode: it is deprecated ) adalah sebuah gereja basilika minor Katolik dan bekas katedral yang terletak di Grado, Friuli Venezia Giulia, Italia. Ini dided...

Chili pepper cultivar 'Siling Labuyo''Siling Labuyo' pepper. The small triangular fruits of siling labuyo are distinctively borne pointing upwards, like other Capsicum frutescens cultivars.GenusCapsicumSpeciesCapsicum frutescensCultivar'Siling Labuyo'Heat Very hotScoville scale80,000 - 100,000 SHU Siling labuyo at a Philippine supermarket Siling labuyo is a small chili pepper cultivar that developed in the Philippines after the Columbian Exchange. It belongs to the species Capsicum ...

Charity Shield FA 1999TurnamenCharity Shield FA Arsenal Manchester United 2 1 Tanggal1 Agustus 1999StadionStadion Wembley, London← 1998 2000 → Charity Shield FA 1999 adalah pertandingan sepak bola antara Arsenal dan Manchester United yang diselenggarakan pada 1 Agustus 1999 di Stadion Wembley, London. Pertandingan ini merupakan pertandingan ke-77 dari penyelenggaraan Charity Shield FA. Pertandingan ini dimenangkan oleh Arsenal dengan skor 2–1.[1][2] Pertandingan ...

منتخب الجزر العذراء الأمريكية لكرة القدم معلومات عامة بلد الرياضة جزر العذراء الأمريكية الفئة كرة القدم للرجال رمز الفيفا VIR الاتحاد اتحاد جزر العذراء الأمريكية لكرة القدم كونفدرالية كونكاكاف (أمريكا الشمالية والوسطى والكاريبي) الموقع الرسمي الموقع الرسمي ...

2003 single by Martina McBrideIn My Daughter's EyesSingle by Martina McBridefrom the album Martina ReleasedNovember 17, 2003 (2003-11-17)Recorded2003; Blackbird Studio(Nashville)GenreCountryLength3:15LabelRCA NashvilleSongwriter(s)James T. SlaterProducer(s) Martina McBride Paul Worley Martina McBride singles chronology This One's for the Girls (2003) In My Daughter's Eyes (2003) How Far (2004) In My Daughter's Eyes is a song written by James T. Slater and recorded by American c...

Rumah Sakit Umum DaerahSawah BesarPemerintah DKI JakartaGeografiLokasiJl. Dwi Warna Raya No. 6-8, Karang Anyar, Kec. Sawah Besar, Jakarta Pusat, DKI Jakarta, IndonesiaOrganisasiAsuransi kesehatanBPJS KesehatanPendanaanRumah sakit publikJenisRumah Sakit Umum DaerahAfiliasi dengan universitasDirektorat Jenderal Pelayanan KesehatanPelayananStandar pelayanan (tingkat Utama)berlaku sampai 2022[1] Ranjang pasien50SejarahDibuka1 April 2015; 8 tahun lalu (2015-04-01) RSUD Sawah Besar ada...

Volcanic mountain in Chile SollipulliAerial photograph of volcan Sollipulli, looking southeast. The dark red feature on the side of Sollipulli is the cinder cone called Chufquen which formed during the most recent eruption, about 700 years ago.Highest pointElevation2,282 m (7,487 ft)[1]ListingList of volcanoes in ChileCoordinates38°58′30″S 71°31′12″W / 38.97500°S 71.52000°W / -38.97500; -71.52000[1]GeographySollipulliLocation ...

Dr.Perdie M. YosephM.A. Bupati Murung Raya ke-2Masa jabatan24 September 2018 – 24 September 2023WakilRejikinnorPendahuluSyarkawi H. Sibu (plh.)Yuel Tanggara (pj.)PenggantiHermon (pj.)Masa jabatan26 Juli 2013 – 26 Juli 2018WakilDarmajiPendahuluWilly Midel YosephPenggantiSyarkawi H. Sibu (plh.)Yuel Tanggara (pj.) Informasi pribadiLahir21 Agustus 1970 (umur 53)Partai politikPDI-PAlma materUniversitas Gadjah Mada[1]PekerjaanPolitikusSunting kotak info �...

Christína MetaxáChristína Metaxá à Moscou en 2009BiographieNaissance 4 avril 1992 (32 ans)LimassolNationalité chyprioteFormation Université BrownActivité ChanteusePériode d'activité depuis 2008Autres informationsGenre artistique PopSite web www.christinametaxa.commodifier - modifier le code - modifier Wikidata Christína Metaxá (grec moderne : Χριστίνα Μεταξά) est une chanteuse chypriote née à Limassol. Eurovision 2009 Elle représente Chypre lors de la se...

Lists of Italian films 1910s 1910 1911 1912 1913 19141915 1916 1917 1918 1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 1994199...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يونيو 2023) يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة ...

Stadium in Clearwater, Florida Clearwater Athletic FieldFormer namesBrooklyn FieldLocationPennsylvania Ave and Seminole St, Clearwater, FloridaCoordinates27°58′25″N 82°47′34″W / 27.973680°N 82.792890°W / 27.973680; -82.792890OwnerCity of ClearwaterCapacity3,100 (1951-1954)Field sizeLeft – 340 ft. Center – ft. Right – 290 ft.SurfacegrassConstructionBroke groundDecember 1922OpenedMarch 15, 1923Closed1954Demolished1956Construction cost$25,000TenantsBrook...

Elections in Syria 2017 Northern Syria Local Elections ← 2015 September 22, 2017 (2017-09-22) Dec 2017 → Turnout70%[1] Regions of the DFNS where elections took place in red Politics of Autonomous Administration of North and East Syria Symbols Symbols of Rojava Constitution Libertarian socialism Human rights Legislature and Government Syrian Democratic Council Executive Council Elections March 2015 (Local) September 2017 (Local) December 2017 (Regio...

American football player and sports coach (1878–1948) Frank CayouCayou at Wabash, c. 1907Biographical detailsBorn(1878-03-07)March 7, 1878Decatur, Nebraska, U.S.DiedMay 7, 1948(1948-05-07) (aged 70)[1]Hominy, Oklahoma, U.S.Playing careerFootball1895–1898Carlisle1898Dickinson1899–1901IllinoisTrack and field1896–1898Carlisle1899Dickinson1900–1902Illinois Position(s)Quarterback, running backCoaching career (HC unless noted)Football1902Champaign Central HS (IL)1904–1907Wa...

New Zealand minister of the Crown The Minister of Lands in New Zealand was a cabinet position appointed by the Prime Minister to be in charge of the Department of Lands and Survey. List of ministers The following ministers held the office of Minister of Lands.[1] Key Independent Liberal Reform United Labour National No. Name Portrait Term of Office Prime Minister 1 Henry Tancred 19 August 1858 12 July 1861 Staffor...

In this Chinese name, the family name is Xue (薛). Joker Xue薛之谦Xue in December 2019Born (1983-07-17) 17 July 1983 (age 40)Shanghai, ChinaNationalityChineseAlma materGlion Institute of Higher EducationOccupationsSinger-songwriterrecord producerYears active2005–presentNotable work演员 Actor, 丑八怪 UglySpouses Leixin Gao (m. 2012–2015) Leixin Gao (m. 2017) Children1Chinese nameSimpli...

Not to be confused with Bentworth. Human settlement in EnglandBetchworthThe Street, BetchworthThe Grade I-listed St Michael's ChurchBetchworthLocation within SurreyArea9.91 km2 (3.83 sq mi)Population1,052 (Civil Parish 2011)[1]• Density106/km2 (270/sq mi)OS grid referenceTQ2150Civil parishBetchworthDistrictMole ValleyShire countySurreyRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townBETCHWORTHPostcode district...

دورات الماسترز 1000 نقطةمعلومات عامةصنف فرعي من دورة كرة مضرب جزء من رابطة محترفي كرة المضرب البداية 2009 الاسم المختصر Masters 1000 (بالإنجليزية) الرياضة كرة المضرب حلَّ محل ATP Masters Series (en) المنظم رابطة محترفي التنس لديه جزء أو أجزاء 2021 Mutua Madrid Open (men) (en) تعديل - تعديل مصدري - تعديل ويكي �...