Category of sets
|
Read other articles:

Daniella Levine Cava Daniella Levine Cava (lahir 14 September 1955) adalah seorang pengacara, pekerja sosial dan politikus Amerika Serikat. Ia menjabat sebagai walikota Miami-Dade County, Florida sejak 2020.[1] Referensi ^ About Commissioner Daniella Levine Cava. www.miamidade.gov. Diarsipkan dari versi asli tanggal 2021-06-25. Diakses tanggal 2020-09-05.

Pour les articles homonymes, voir Sambre-et-Meuse (homonymie). Carte (CIA 1968) des ressources en Belgique. Le sillon Sambre-et-Meuse et les zones avoisinantes riches en charbon ont déterminé les régions industrielles. Le sillon Sambre-et-Meuse est la partie apparente en Belgique de ce que les géologues appellent la « Faille du midi » ou « Grande faille du midi » (ou « Bande de Sambre-et-Meuse »[1], « Bande condruzienne »[1], « Bande ...

Pour les articles homonymes, voir Watford (homonymie). Watford L'église Sainte-Marie Administration Pays Royaume-Uni Nation Angleterre Comté Hertfordshire Maire Peter Taylor (élu en 2018) Code postal WD Indicatif 01923 & 020 Démographie Population 79 300 hab. (2005) Densité 3 776 hab./km2 Géographie Coordonnées 51° 39′ 19″ nord, 0° 23′ 45″ ouest Altitude 71 m Superficie 2 100 ha = 21 km2 Loca...

1924 film by Louis J. Gasnier The TriflersAdvertisementDirected byLouis GasnierWritten byEve UnsellJohn F. GoodrichBased onThe Triflersby Frederick Orin BartlettProduced byB. P. SchulbergStarringMae BuschCinematographyWilliam TuersDistributed byPreferred PicturesAl LichtmanRelease date December 15, 1924 (1924-12-15) Running time70 min.CountryUnited StatesLanguageSilent (English intertitles) The Triflers is a 1924 American silent society drama film directed by Louis Gasnier and ...

Pair of goats in Norse mythology The goats Tanngrisnir and Tanngnjóstr pull the chariot of the god Thor in an illustration from 1832. Tanngrisnir (Old Norse: [ˈtɑnːˌɡrisnez̠], literal meaning teeth grinder or one that grinds teeth) and Tanngnjóstr ([ˈtɑnːˌɡnjoːstz̠], teeth thin, or one that has gaps between the teeth) are the goats who pull the chariot of the god Thor in Norse mythology. They are attested in the Poetic Edda, compiled in the 13th century from ear...

Not to be confused with Snowy Mountains or Snowy Mountain. Dam in Kosciuszko National Park, New South WalesSnowy Mountains SchemeMap of Snowy Mountains SchemeCountryAustraliaLocationKosciuszko National Park, New South WalesCoordinates36°07′S 148°36′E / 36.12°S 148.6°E / -36.12; 148.6PurposeHydroelectricity and irrigation projectStatusOperationalConstruction began17 October 1949 (1949-10-17)Opening date21 October 1972 (197...

Arborescence des biographies ↑ · ↓ Catégorie mère Portail Projet Café Arborescence du cinéma américain ↑ · ↓ Catégorie mère Projet Portail Café Arborescence réalisation audiovisuelle ↑ · ↓ Réalisateur et Réalisatrice Projet Portail Voir aussi la catégorie « Réalisatrice américaine » pour les personnalités féminines. Le contenu de cette catégorie devrait être diffusé vers ses sous-catégories. Certains des articles qui figurent dans...

Alan G. PoindexterLahirAlan Goodwin Poindexter(1961-11-05)5 November 1961Pasadena, California, ASStatusAlmarhumMeninggal1 Juli 2012(2012-07-01) (umur 50)Pensacola Beach, Florida, ASKebangsaanAmerika SerikatAlmamaterPensacola Junior College, A.S. 1983Georgia Institute of Technology, B.S. 1986Naval Postgraduate School, M.S. 1995PekerjaanPilot uji coba, penerbang angkatan lautKarier luar angkasaAntariksawan NASAPangkat Kapten Angkatan Laut Amerika SerikatWaktu di luar angkasa27 hari 21 jam...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2016. Berikut ini adalah daftar operasi militer di Eropa pada bagian Timur. Ini adalah operasi Jerman dan sekutu-sekutunya di satu sisi serta Uni Soviet dan sekutu-sekutunya di pihak lain sebagai konsekuensi dari invasi Jerman pada tahun 1941. Finlandia, dik...

H.Syah AfandinS.H. Pelaksana Tugas Bupati LangkatPetahanaMulai menjabat 20 Januari 2022PresidenJoko WidodoGubernurEdy RahmayadiPendahuluTerbit Rencana Perangin AnginPenggantiPetahana Wakil Bupati Langkat ke-4Masa jabatan20 Februari 2019 – 20 Januari 2022PresidenJoko WidodoGubernurEdy RahmayadiBupatiTerbit Rencana Perangin AnginPendahuluSulistiyantoPenggantiPetahana Informasi pribadiLahir23 Juni 1966 (umur 57)Pangkalan Brandan, Sumatera UtaraKebangsaanIndonesiaPartai po...

Form of Yemeni Arabic spoken in Sanaa Sanʽani ArabicNative toYemenSpeakers13 million (2020)[1]Language familyAfro-Asiatic SemiticWest SemiticCentral SemiticArabicPeninsularYemeniSanʽani ArabicWriting systemArabic alphabetLanguage codesISO 639-3aynGlottologsana1295Distribution of Sanʽani Arabic according to EthnologueThis article contains IPA phonetic symbols. Without proper rendering support, you may see question marks, boxes, or other symbols instead of Unicode character...

Israeli restaurant in Philadelphia, Pennsylvania ZahavRestaurant informationEstablished2008 (2008)Owner(s)Steven CookMichael SolomonovHead chefMichael SolomonovFood typeIsraeli cuisineJewish cuisineDress codeCasualRatingGayot: 14/20Street address237 St James PlCityPhiladelphiaStatePennsylvaniaPostal/ZIP Code19106ReservationsrecommendedWebsitewww.zahavrestaurant.com Zahav (from Hebrew: זהב zahav, lit. gold) is an Israeli restaurant in Philadelphia founded in 2008. It is managed by head...
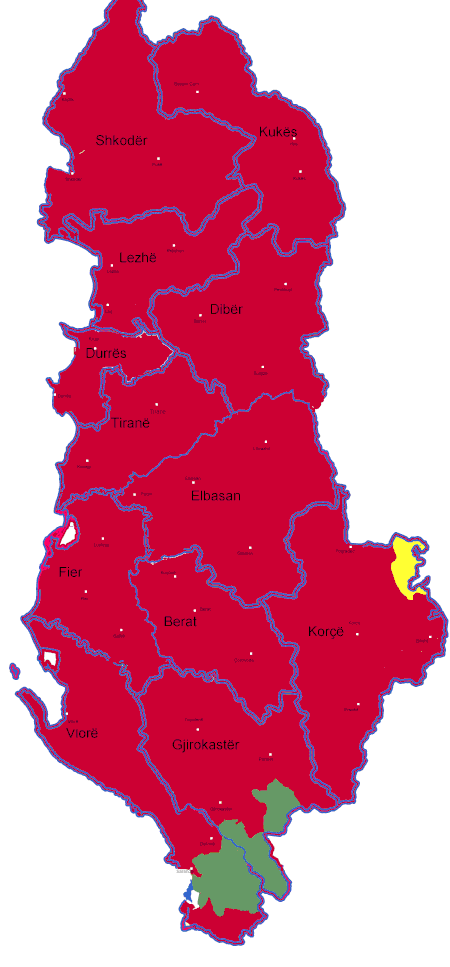
La demografía de Albania estudia estadísticamente la estructura y la dinámica de la población residente en el territorio albanés, así como los procesos que la determinan: fecundidad, mortalidad y migración en dicho territorio.[1] Paisaje rural en Shkodra, Albania Población La población albanesa no tiene un marcado carácter urbano, como sucede en otros países europeos ya que la mitad de su población activa se dedica a la agricultura. Generalmente residen en zonas de altitud ...

Voce principale: Offenbacher Fußball-Club Kickers 1901. Offenbacher Fußball-Club Kickers 1901Stagione 1975-1976Sport calcio Squadra Kickers Offenbach Allenatore Otto Rehhagel (1ª-17ª) Zlatko Čajkovski (18ª-34ª) Bundesliga17º posto Coppa di GermaniaPrimo turno Maggiori presenzeCampionato: Rausch, Held, Bitz, Helmschrot, Hickersberger (34)Totale: Rausch, Held, Bitz, Helmschrot, Hickersberger (35) Miglior marcatoreCampionato: Janzon (9)Totale: Janzon (9) StadioStadion am Bieberer B...

Sapfo atau Lesbos, dilukis tahun 1904 oleh John William Godward, memberi istilah lesbian yang berkonotasi hasrat erotis antara sesama wanita.[1] Sastra lesbian adalah subgenre dari sastra yang membahas tema lesbian, termasuk puisi, drama, karya-karya fiksi yang membahas karakter lesbian, dan karya-karya non-fiksi tentang topik lesbian. Fiksi yang termasuk dalam kategori ini bisa dari genre apa saja, misalnya fiksi sejarah, fiksi ilmiah, fantasi, horor, atau roman. Beberapa penulis pri...

County in Kentucky, United States County in KentuckyBallard CountyCountyBallard County Courthouse in WickliffeLocation within the U.S. state of KentuckyKentucky's location within the U.S.Coordinates: 37°04′N 89°00′W / 37.06°N 89°W / 37.06; -89Country United StatesState KentuckyFounded1842Named forBland BallardSeatWickliffeLargest cityLaCenterArea • Total274 sq mi (710 km2) • Land247 sq mi (640 km2)...

Line of smartphones by Apple Inc. For other uses, see IPhone (disambiguation). iPhoneFront face of the latest model, the iPhone 15 ProDeveloperAppleManufacturerContract manufacturers: FoxconnPegatronWistronTata GroupTypeSmartphoneUnits sold2.3 billion (as of January 1, 2024[update])[1]Operating systemiOSStorage64, 128, 256, 512 GB or 1 TB[note 1] flash memory[2] (current models)Sound Bluetooth stereo speaker (iPhone 7 and up) microphone ...

Nickname for the Southern United States For the 19th-century song, see Dixie (song). For the cultural and geographic subregion of the southern United States, see Deep South. For other uses, see Dixie (disambiguation) and Dixieland (disambiguation). M.E. Garrison's Map of Dixie published in 1909. This version of Dixie only includes states within the Southeast, omitting traditionally included states such as Texas or Virginia. Dixie, also known as Dixieland or Dixie's Land, is a nickname for all...

2020 South Korean TV series This article is about South Korean drama on tvN. For South Korean reality television show on SBS, see Oh! My Baby. Not to be confused with My Little Baby. Oh My BabyPromotional posterHangul오 마이 베이비 GenreRomantic comedyWritten byNo Sun-jaeDirected byNam Ki-hoonStarringJang Na-raGo JunPark Byung-eunJung Gun-jooCountry of originSouth KoreaOriginal languageKoreanNo. of episodes16ProductionRunning time63-70 minutesProduction companiesStudio&NEWStudio Dra...

Shahih Muslim PengarangMuslim bin al-HajjajNegaraPersiaBahasaArabSubjekHadisGenreKumpulan hadisDiterbitkanabad ke-9 Al-Jami' atau biasa dikenal dengan Shahih Muslim merupakan kitab (buku) koleksi hadis yang disusun oleh Muslim bin al-Hajjaj yang hidup antara 202 hingga 261 hijriah.[1] Ia merupakan murid dari Imam Bukhari. Koleksi hadis ini di kalangan muslim Sunni adalah koleksi terbaik kedua setelah Shahih Bukhari. Dari sekitar 300.000 hadis yang ia kumpulkan hanya sekitar 4000 yang ...
