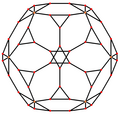
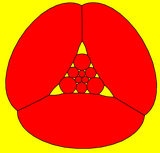
Зрізаний додекаедр
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Eduardo Gadiano Gubernur Mindoro BaratPetahanaMulai menjabat 30 Juni 2019PresidenRodrigo Duterte PendahuluMario Gene MendiolaPenggantiPetahanaWalikota SablayanMasa jabatan2010–2019 PendahuluGodofredo B. MintuPenggantiAndres D. Dangeros Informasi ...

Coat trait found in some horses Pangare traits include light underparts and light muzzle Pangare traits are most visible on the belly Fjord horses usually express the pangaré trait. Pangare is less obvious on a short-haired coat Pangaré is a coat trait found in some horses that features pale hair around the eyes, muzzle, and underside of the body. These pale areas can extend up to the flanks, throat and chest, behind the elbows, in front of the stifle, and up the buttock.[1] Animals...

Kabupaten SelumaKabupatenSalah satu sudut hutan lindung di Seluma LambangMotto: Serawai serasan seijoan(Serawai) Satu rumpun, satu mufakat, dan satu musyawarahPetaKabupaten SelumaPetaTampilkan peta SumatraKabupaten SelumaKabupaten Seluma (Indonesia)Tampilkan peta IndonesiaKoordinat: 3°57′59″S 102°28′27″E / 3.96644°S 102.47429°E / -3.96644; 102.47429Negara IndonesiaProvinsiBengkuluTanggal berdiri25 Februari 2003[1]Dasar hukumUU Nomor 3 Tahu...

Untuk ayah dari raja tersebut, lihat John I de Balliol. Untuk permainan panggung 1825, lihat John Balliol (permainan panggung). John BalliolRaja John, mahkota dan tongkatnya secara simbolik dipatahkan dan dengan lambang kosong, tergambarkan dalam Forman Armorial tahun 1562, yang diproduksi untuk Mary, Ratu SkotlandiaRaja SkotlandiaBerkuasa17 November 1292 – 10 Juli 1296Penobatan30 November 1292PendahuluMargaretPenerusRobert I (sebagai Raja Skotlandia) William Wallace(sebagai Penjaga Skotlan...

Borgo Vercelli commune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Vercelli NegaraItalia Ibu kotaBorgo Vercelli PendudukTotal2.256 (2023 )GeografiLuas wilayah19,3 km² [convert: unit tak dikenal]Ketinggian126 m Berbatasan denganCasalino Casalvolone Vercelli Villata Vinzaglio SejarahSanto pelindungMaria Diangkat ke Surga Informasi tambahanKode pos13012 Zona waktuUTC+1 UTC+2 Kode telepon0161 ID ISTAT002017 Kode kadaster ItaliaB046 Lain-la...

Untuk pengertian lain, lihat Bantimurung (disambiguasi). Taman NasionalBantimurung-BulusaraungIUCN Kategori II (Taman Nasional)Pemandangan tebing di TN Babul Logo TN BabulTN BabulLokasi di SulawesiLetakKabupaten Maros, Kabupaten Pangkep & Kabupaten Bone, Sulawesi Selatan, IndonesiaKota terdekatKota Turikale (13 km)Kota PangkajeneKota WatamponeKota Makassar (28 km)Koordinat4°54′S 119°45′E / 4.900°S 119.750°E / -4.900; 119.750Koordinat: 4°54′S 119°45′E&...

Edward Vincent DarginAuxiliary Bishop of New YorkIn office1953-1973OrdersOrdinationSeptember 23, 1922by Cardinal Patrick Joseph HayesConsecrationOctober 5, 1954by Cardinal James Francis McIntyrePersonal detailsBorn(1898-04-25)April 25, 1898New York CityDiedApril 20, 1981(1981-04-20) (aged 82)Mary Manning Walsh HomeBuriedOur Lady of Mercy CemeteryNationalityAmericanDenominationRoman CatholicEducationFordham UniversityAlma materSt. Joseph's Seminary Edward Vincent Dargin (April 2...

Masonic Hall in New York City is the headquarters of the Grand Lodge of Free and Accepted Masons of the State of New York. It has been located at 23rd Street and 6th Avenue in the Flatiron district[1] since 1875. The current building, completed in two phases, dates from 1909 and 1913. The first Masonic Hall was a Gothic style building located in lower Manhattan, constructed in 1826. The second Masonic Hall was built in 1875 and designed by Napoleon LeBrun and constructed in the Second...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Arzachena Alzachèna, AltzaghènaKomuneComune di ArzachenaLokasi Arzachena di Provinsi SassariNegaraItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaRoberto RagneddaLuas • Total230,85 km2 (89,13 sq mi)Ketinggian85 m (279 ft)Populasi (2016) • Total13,650[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07020-21Kode area telepon0789Situs webhttp://www.comunearzachena.it/ Arzachen...

Joseph Gardner SwiftColonel Joseph Gardner SwiftBorn(1783-12-31)December 31, 1783Nantucket, MassachusettsDiedJuly 22, 1865(1865-07-22) (aged 81)Geneva, New YorkAllegianceUnited States of AmericaService/branchUnited States ArmyYears of service1802–1818RankColonelBrevet brigadier generalCommands heldConstruction of Cape Fear River defensesFort Johnson, North CarolinaSuperintendent of the United States Military AcademyEastern Department DefensesChief Engineer of the US ArmyBattles/w...

San Siro, the home of AC Milan and Internazionale. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of football stadiums in Italy – news · newspapers · books · scholar · JSTOR (March 2011) (Learn how and when to remove this message) There are 64 football stadiums in Italy which have a capacity of 10,000 ...

Сергіївський парк 46°01′08″ пн. ш. 30°21′20″ сх. д. / 46.018890000027774079° пн. ш. 30.35583000002777965° сх. д. / 46.018890000027774079; 30.35583000002777965Координати: 46°01′08″ пн. ш. 30°21′20″ сх. д. / 46.018890000027774079° пн. ш. 30.35583000002777965° сх. д. / 46.018890000027774079; 30.35...

Santa Luciastazione ferroviariaMost na Soči LocalizzazioneStato Slovenia LocalitàSanta Lucia Coordinate46°08′47.81″N 13°45′34.49″E46°08′47.81″N, 13°45′34.49″E Lineeferrovia Jesenice-Trieste StoriaStato attualein uso Attivazione1906 CaratteristicheTipostazione in superficie, passante OperatoriSlovenske železnice Modifica dati su Wikidata · Manuale La stazione di Santa Lucia (in sloveno Most na Soči), in passato anche Stazione di Santa Lucia-Tolmino, Staz...

Clairo Clairo во время выступления в Осло, 2019 год Основная информация Имя при рождении Клэр Элизабет Коттрилл Дата рождения 18 августа 1998(1998-08-18) (25 лет) Место рождения Атланта Страна США Профессии автор-исполнитель Годы активности 2012 — н. в. Инструменты Гитара, к...

آنا ماغناني (بالإيطالية: Anna Magnani) معلومات شخصية الميلاد 7 مارس 1908(1908-03-07)روما، مملكة إيطاليا الوفاة 26 سبتمبر 1973 (65 سنة)روما، إيطاليا سبب الوفاة ورم البنكرياس الجنسية إيطاليا الزوج جوفريدو أليساندريني (1935–1950) عدد الأولاد 1 الحياة العملية المدرسة الأم أكاديمية سيل�...

العلاقات الرواندية الناميبية رواندا ناميبيا رواندا ناميبيا تعديل مصدري - تعديل العلاقات الرواندية الناميبية هي العلاقات الثنائية التي تجمع بين رواندا وناميبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Lissabon (Begriffsklärung) aufgeführt. Lissabon Wappen Karte Lissabon (Portugal) Basisdaten Region: Lisboa Unterregion: Metropolregion Lissabon Distrikt: Lissabon Concelho: Lisboa Koordinaten: 38° 43′ N, 9° 10′ W38.716666666667-9.1666666666667Koordinaten: 38° 43′ N, 9° 10′ W Einwohner: 545.796 (Stand: 19. April 2021)[1] Fläche: 100,03 km² (St...

German poet and dramatist (1746–1797) Friedrich Wilhelm Gotter (3 September 1746 – 18 March 1797) was a German poet, dramatist, and opera librettist.[1] Biography He was born at Gotha. He started out studying law, but early on was influenced to write for the theatre.[2] After the completion of his university course at Göttingen, he was appointed second director of the Gotha Archive. He subsequently went to Wetzlar, the seat of the imperial law courts, as secretary to the ...

American landscape architect (born 1938) Laurie OlinBorn (1938-10-12) 12 October 1938 (age 85)Marshfield, WisconsinNationalityAmericanAlma materUniversity of WashingtonOccupationArchitectAwardsThomas Jefferson Medal in Architecture 2013 PracticeThe Olin StudioDesignLandscape architecture Laurie Olin (born 1938, Marshfield, Wisconsin) is an American landscape architect. He has worked on landscape design projects at diverse scales, from private residential gardens to public parks and ...