Теселяція
|
Read other articles:

Doni AkbarS.E. Anggota Dewan Perwakilan Rakyat Republik IndonesiaPetahanaMulai menjabat 1 Oktober 2019PresidenJoko WidodoDaerah pemilihanJawa Tengah X Informasi pribadiLahir9 Juli 1982 (umur 41)Palembang, Sumatera SelatanPartai politikGolkarSuami/istriSandraningrum TriputrantiAnak2Alma materUniversitas TrisaktiPekerjaanDirektur, Komisaris, PolitikusSunting kotak info • L • B Doni Akbar, S.E. (lahir 9 Juli 1982) adalah politikus Indonesia yang menjabat sebagai anggota DP...

Kunjungan Xi Jinping ke Rusia 2023Putin menyambut Xi di Moskwa, 21 Maret 2023Tanggal20–22 Maret 2023 (2023-3-22)LokasiMoskwa, Rusia Pada tanggal 20-22 Maret 2023, Xi Jinping, sekretaris jenderal Partai Komunis Tiongkok dan presiden Republik Rakyat Tiongkok, mengunjungi Rusia, dalam pertemuan internasional pertamanya sejak terpilih kembali sebagai presiden pada Kongres Rakyat Nasional 2023. Ia bertemu dengan Presiden Rusia Vladimir Putin baik dalam kapasitas resmi maupun tidak resmi. In...

State highway in Massachusetts, US Route 107Route 107 highlighted in redRoute informationMaintained by MassDOTLength11.9 mi[1] (19.2 km)Existed1930–presentMajor junctionsSouth end Route 16 at Revere-Chelsea borderMajor intersections Route 60 in Revere Route 129 in Lynn Route 129A in Lynn Route 114 in Salem North end Route 1A at Salem-Beverly border LocationCountryUnited StatesStateMassachusettsCountiesSuffolk, Essex Highway syst...

Thoroughfare in Toronto, Ontario For the avenue in Delaware County, Pennsylvania, see State Route 2005 (Delaware County, Pennsylvania). Lansdowne AvenueLansdowne Avenue in TorontoLooking north along Lansdowne AvenueRoute informationMaintained by City of Toronto governmentMajor junctionsSouth endQueen StreetMajor intersectionsDundas StreetBloor StreetDupont StreetNorth endSt. Clair Avenue LocationCountryCanadaProvinceOntario Highway system Roads in Toronto North–South East–West D...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sou...

Wilhelm Miklas Presiden AustriaMasa jabatan10 Desember 1928 – 13 Maret 1938KanselirIgnaz SeipelErnst StreeruwitzJohann SchoberKarl VaugoinOtto EnderKarl BureschEngelbert DollfußKurt SchuschniggArthur Seyss-Inquart PendahuluMichael HainischPenggantiKarl Renner (1945)Presiden Dewan NasionalMasa jabatan20 November 1923 – 6 Desember 1928 PendahuluRichard WeiskirchnerPenggantiAlfred GürtlerUnterstaatssekretär PendidikanMasa jabatan7 Juli 1920 – 20 November 1920K...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Jaringan Sekolah Islam Terpadu – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini mungkin mengandung riset asli. Anda dapat membantu memperbaikinya dengan memastikan pernyataan yang dibuat d...

1997 studio album by Electric WizardCome My Fanatics…Studio album by Electric WizardReleasedJanuary 1997 (1997-01)RecordedJuly 1996StudioRed Dog Studios, BournemouthGenreDoom metalstoner metalLength49:43LabelRise AboveProducerJus ObornRolf StartinMike HurstElectric Wizard chronology Electric Wizard/Our Haunted Kingdom(1996) Come My Fanatics…(1997) Chrono.Naut(1997) Original cover Come My Fanatics… is the second studio album by English heavy metal band Electric Wizard....

Pasukan Jepang mendarat di Andaman, Maret 1942. Pendudukan Jepang di Kepulauan Andaman terjadi pada tahun 1942 saat Perang Dunia II sedang berlangsung. Kepulauan Andaman dan Nikobar (dengan luas sebesar 8,293 km2 dari 139 pulau), adalah sekelompok pulau yang terletak di Teluk Benggala sekitar 1.250 km (780 mi) dari Kolkata, 1.200 km (750 mi) dari Chennai dan 190 km (120 mi) dari Cape Nargis di Burma. Hingga tahun 1938, pemerintah Inggris menjadikan wilayah K...

National forest in California, US Klamath National ForestLittle Elk Lake in Klamath National ForestMap of the United StatesLocationSiskiyou County, California / Jackson County, OregonNearest cityYreka, CaliforniaCoordinates41°30′01″N 123°20′00″W / 41.50028°N 123.33333°W / 41.50028; -123.33333Area1,737,774 acres (7,032.52 km2)Governing bodyU.S. Forest ServiceWebsiteKlamath National Forest Klamath National Forest is a 1,737,774-acre (2,715 ...

Not to be confused with 2023 Leagues Cup final. Football match2023 EFL Cup finalWembley Stadium hosted the matchEvent2022–23 EFL Cup Manchester United Newcastle United 2 0 Date26 February 2023 (2023-02-26)VenueWembley Stadium, LondonMan of the MatchCasemiro (Manchester United)[1]RefereeDavid Coote (Nottinghamshire)[2]Attendance87,306[3]← 2022 2024 → The 2023 EFL Cup final was the final of the 2022–23 EFL Cup. It was played between Manche...

RitterKarl Ernst von BaerLahir28 February [K.J.: 17] 1792[butuh rujukan]Piep, Kreis Jerwen, Governorate of Estonia, Kekaisaran Rusia( Piibe masa kini, Lääne-Viru, Estonia)Meninggal28 November [K.J.: 16 November] 1876 (84 tahun)Dorpat, Governorate of Livonia, Kekaisaran Rusia(sekarang Tartu, Estonia)KebangsaanJerman BaltikAlmamaterUniversitas Imperial DorpatDikenal atasPenemuan sel telur mamaliaMenjelajahi Rusia Eropa dan SkandinaviaHukum von BaerHukum Baer–BabinetKarier ilmiahBid...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

此條目可参照英語維基百科相應條目来扩充。 (2023年12月1日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此條目需要补充更多来源。 (2021年4月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能�...

Grangeston HaltGrangeston Halt looking towards AyrGeneral informationLocationBetween Killochan and GirvanScotlandCoordinates55°15′31″N 4°49′40″W / 55.25871°N 4.82785°W / 55.25871; -4.82785Grid referenceNX203997Platforms2Other informationStatusDisusedHistoryOriginal companyLondon, Midland and Scottish RailwayKey dates15 December 1941Opened1965Closed[1] The Grangeston Halt railway station was a private station that was not listed in the public timeta...

Mammalian protein found in Homo sapiens This article is about the glycoprotein. For the stimulant drug, see G-130. Cd130 redirects here. For the isotope of cadmium (Cd-130 or 130Cd), see Cadmium-130. IL6STAvailable structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1BJ8, 1BQU, 1I1R, 1P9M, 1PVH, 3L5H, 3L5I, 3L5J,%%s1BJ8, 1BQU, 1I1R, 1P9M, 1PVH, 3L5H, 3L5I, 3L5J, 1N2QIdentifiersAliasesIL6ST, CD130, CDW130, GP130, IL-6RB, interleukin 6 signal transducerExternal IDsOMIM: 600694 MGI: 9656...

1981 Dutch general election ← 1977 26 May 1981 1982 → All 150 seats in the House of Representatives76 seats needed for a majorityTurnout87.0% ( 1.1 pp) Party Leader % Seats +/– CDA Dries van Agt 30.8% 48 −1 PvdA Joop den Uyl 28.3% 44 −9 VVD Hans Wiegel 17.3% 26 −2 D66 Jan Terlouw 11.1% 17 +9 PSP Fred van der Spek 2.1% 3 +2 CPN Marcus Bakker 2.1% 3 +1 SGP Henk van Rossum 2.0% 3 0 PPR Ria Beckers 2.0% 3 0 RPF Meindert Leerling 1.2% 2 +2 GPV Gert Schutte 0.8% 1 0 T...
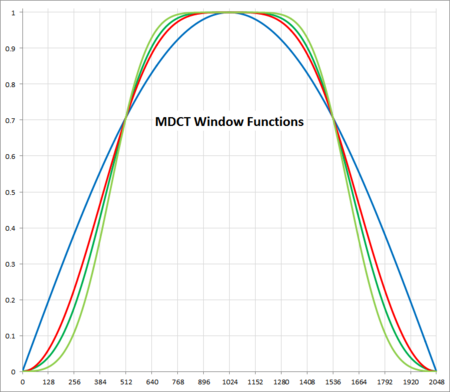
Mathematical transform using in signal processing MDCT redirects here. For the form of medical imaging, see Multidetector computed tomography. The modified discrete cosine transform (MDCT) is a transform based on the type-IV discrete cosine transform (DCT-IV), with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset, where subsequent blocks are overlapped so that the last half of one block coincides with the first half of the next ...

Palazzo delle PaurePalazzo della DoganaLocalizzazioneStato Italia RegioneLombardia LocalitàLecco IndirizzoPiazza XX Settembre, 22 Coordinate45°51′19.16″N 9°23′21.85″E45°51′19.16″N, 9°23′21.85″E Informazioni generaliCondizioniin uso Costruzione1905 Ricostruzione1916 (torre 1926) StileEclettico neomedievale UsoPolo museale (precedentemente si trovavano gli uffici del catasto, delle imposte e della dogana) Piani4 RealizzazioneProprietarioComune di Lecco CommittenteInten...