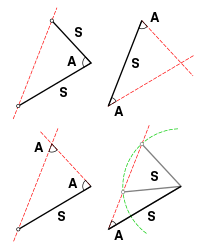
Конгруентність (геометрія)
|
Read other articles:

Las coordenadas geográficas son un sistema de referencia que permite que cada ubicación en la Tierra sea especificada por un conjunto de números, letras o símbolos. Las coordenadas se eligen, en general, de manera que las dos referencias representen una posición horizontal y una tercera que represente la altitud. Las coordenadas de posición horizontal utilizadas son la latitud y longitud, un sistema de coordenadas angulares esféricas o esferoides cuyo centro es el centro de la Tierra y...

Djoko Tjahjono Wakapuslaiklambangjaau Informasi pribadiLahir9 Maret 1968 (umur 56)Surabaya, Jawa TimurKebangsaanIndonesiaAlma materAkademi Angkatan Udara (1990)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan UdaraMasa dinas1990—sekarangPangkat Marsekal Pertama TNISatuanKorps Penerbang (Tempur)Sunting kotak info • L • B Marsekal Pertama TNI Djoko Tjahjono, S.E, M.M. (lahir 9 Maret 1968) adalah seorang perwira tinggi TNI-AU yang sejak 29 Maret 2023 mengemba...

Struktur gugus fungsional hidrazona Hidrazona adalah suatu kelas senyawa organik dengan struktur R1R2C=NNH2.[1] Senyawaan ini mirip dengan keton dan aldehida dengan penggantian atom oksigen dengan gugus fungsi NNH2. Senyawa ini biasanya terbentuk sebagai reaksi antara suatu hidrazina dengan keton atau aldehida.[2][3] Aplikasi Pembentukan turunan hidrazona aromatik digunakan untuk mengukur konsentrasi aldehida dan keton dengan berat molekul rendah, misalnya dalam aliran...

راتشفيل الإحداثيات 42°45′40″N 77°13′34″W / 42.7611°N 77.2261°W / 42.7611; -77.2261 [1] تاريخ التأسيس 1866 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى نيويورك خصائص جغرافية المساحة 1.655814 كيلومتر مربع1.655816 كيلومتر مربع (1 أبريل 2010) ارتفاع 26...

عملية أتلانتا جزء من القرصنة في القرن الإفريقي التاريخ 8 ديسمبر 2008 الموقع خليج عدن تعديل مصدري - تعديل مناطق القرصنة في المحيط الهندي. عملية أتلانتا هي عملية عسكرية حالية تقوم بها القوة البحرية التابعة للاتحاد الأوروبي تهدف إلى منع ومُكافحة أعمال القرص...

French historian Patrick BoucheronPatrick Boucheron in 2016Born (1965-10-28) 28 October 1965 (age 58)Paris, FranceEducationLycée Marcelin BerthelotLycée Henri IVAlma materÉcole normale supérieure de lettres et sciences humainesOccupationHistorianEmployerCollège de France Patrick Boucheron (born 28 October 1965)[1][2] is a French historian. He previously taught medieval history at the École normale supérieure and the University of Paris. He is a professor of hi...

Hōjō Ujitsuna Hōjō Ujitsuna[1] (北条 氏綱?; 1487 – 10 agosto 1541) fu il figlio maggiore di Hōjō Sōun, fondatore del clan Hōjō. Continuò l'opera del padre di conquista e controllo del Kantō. Ujitsuna fu il secondo daimyō del clan Hōjō e figlio maggiore di Hōjō Sōun (1432-1519). Assunse la guida del clan dopo la morte del padre nel 1519. Quando Ujitsuna divenne daimyō, gli Hōjō controllavano la provincia di Izu, la maggior parte della provincia di Sagami e sta...

Voce principale: Verein für Leibesübungen Wolfsburg (femminile). VfL WolfsburgStagione 2019-2020Sport calcio Squadra Wolfsburg Allenatore Stephan Lerch Presidente Hans Dieter Pötsch Frauen-Bundesliga1º posto (in Women's Champions League) DFB-Pokal der FrauenVincitrice Champions LeagueFinale Maggiori presenzeCampionato: Goeßling (22)Totale: Harder (33) Miglior marcatoreCampionato: Harder (27)Totale: Harder (38) StadioAOK Stadion 2018-2019 2020-2021 Si invita a seguire il modello di ...
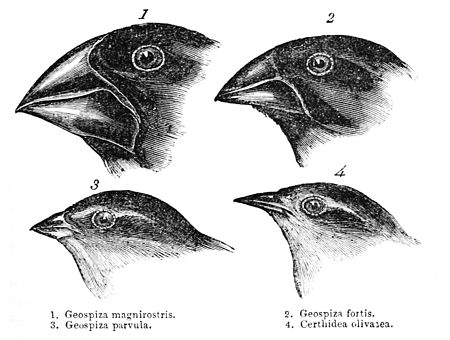
A process in which organisms diversify rapidly from an ancestral species For a more general term to describe any radiation, see Evolutionary radiation. Four of the 14 finch species found in the Galápagos Archipelago, which are thought to have evolved via an adaptive radiation that diversified their beak shapes, enabling them to exploit different food sources. Part of a series onEvolutionary biologyDarwin's finches by John Gould Index Introduction Main Outline Glossary Evidence History Proces...

Cet article est une ébauche concernant un peintre italien. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Giovanni SerodineNaissance 1594 ou 1600Ascona ou RomeDécès 21 décembre 1630RomeActivités Peintre, plâtrier ou plâtrière, sculpteur, architectemodifier - modifier le code - modifier Wikidata Giovanni Serodine, né en 1600 à Ascona et mort le 21 décembre 1630 à Rome, est un peintre de la période b...

此條目可参照英語維基百科相應條目来扩充。 (2017年8月)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 密西西比州 美國联邦州State of Mississippi 州旗州徽綽號:木蘭之州地图中高亮部分为密西西比州坐标:30°13'N�...

2015 EP by AOAHeart AttackEP by AOAReleasedJune 22, 2015Recorded2015GenreK-popelectropopdance-popLength20:34LabelFNCProducerBrave BrothersAOA chronology Like a Cat(2014) Heart Attack(2015) Ace of Angels(2015) Singles from Heart Attack Heart AttackReleased: June 22, 2015 Heart Attack is the third extended play by South Korean girl group AOA, released on June 22, 2015 by FNC Entertainment. The song of the same name was used as the lead single for the album. Singles The song Heart Attack...

L’Oréal Création 30 juillet 1909 (Société française de teintures inoffensives pour cheveux) Dates clés 1920 (nom actuel) Fondateurs Eugène Schueller Personnages clés François Dalle, Charles Zviak, Lindsay Owen-Jones, Jean-Paul Agon, Liliane Bettencourt, Françoise Bettencourt Meyers Forme juridique Société anonyme Action Euronext : OR Slogan Créer la beauté qui fait avancer le monde[1]Parce que je le vaux bien (L'Oréal Paris) Siège social 14, rue Royale, 75008 Pari...

Hong Kong singer and actor This article needs to be updated. Please help update this article to reflect recent events or newly available information. (November 2012) Kenny BeeBornChung Chun-to (1953-02-23) 23 February 1953 (age 71)Hong KongOccupationsMusiciansingersongwriteractorYears active1973–presentSpouses Teresa Cheung (m. 1988; div. 1999) Fan-jiang Su-zhen (m. 2014) Children4Chinese nameTradit...

List of events ← 1976 1975 1974 1977 in India → 1978 1979 1980 Centuries: 18th 19th 20th 21st Decades: 1950s 1960s 1970s 1980s 1990s See also:List of years in IndiaTimeline of Indian history Events in the year 1977 in the Republic of India. Incumbents President of India – Fakhruddin Ali Ahmed until 11 February, Neelam Sanjiva Reddy.[1] Prime Minister of India – Indira Gandhi until 24 March, Morarji Desai.[2] Vice President of India – B.D. Jatti Chief Justice...

British writer and Actress Meera SyalCBE FRSLSyal at the 7th Asian Awards in 2017BornFeroza Syal (1961-06-27) 27 June 1961 (age 62)Wolverhampton, EnglandEducationQueen Mary's High SchoolAlma materUniversity of ManchesterOccupation(s)Comedian, writer, playwright, singer, journalist, actressYears active1983–presentSpouses Shekhar Bhatia (m. 1989; div. 2002) Sanjeev Bhaskar (m. 2005)Children2 ...

Disambiguazione – Elea rimanda qui. Se stai cercando l'antica città del Peloponneso, vedi Elis (Grecia). Elea-VeliaHyeleVista degli scavi archeologiciCiviltàMagna Grecia Epoca541-535 a.C. - fine età imperiale LocalizzazioneStato Italia ComuneAscea DimensioniSuperficie6 000 000 m² AmministrazioneEnteParco archeologico di Paestum e Velia ResponsabileTiziana D'Angelo Visitabilesì Sito webwww.museopaestum.beniculturali.it/ Mappa di localizzazione Modifica dati ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Julian Schauerte Schauerte dengan Fortuna Düsseldorf pada 2014Informasi pribadiTanggal lahir 2 April 1988 (umur 36)Tempat lahir Lennestadt, Jerman BaratPosisi bermain BekInformasi klubKlub saat ini Fortuna DüsseldorfNomor 4Karier junior Grafsch...

Park nel 2012. Park Eun-hye[1] (hangeul: 박은혜; Incheon, 21 febbraio 1978) è un'attrice sudcoreana. Indice 1 Carriera 2 Vita privata 3 Filmografia parziale 3.1 Televisione 3.2 Cinema 4 Note 5 Altri progetti 6 Collegamenti esterni Carriera Park Eun-hye entra nell'industria dell'intrattenimento nel 1998, ma diventa famosa solo nel 2003 grazie ad un ruolo secondario nel serial Dae Jang-geum, che ebbe un incredibile successo in tutta l'Asia[2]. Si impone come icona della Kore...

ProfesorWilliam Stanley JevonsFRSLahir(1835-09-01)1 September 1835Liverpool, Lancashire, InggrisMeninggal13 Agustus 1882(1882-08-13) (umur 46)Bexhill-on-Sea, Sussex, InggrisWarga negaraInggrisAlmamaterUniversity College LondonDikenal atasTeori peralatan marginalParadoks JevonsAnakHerbert Stanley JevonsKarier ilmiahBidangEkonomiLogikaInstitusiUniversity College London (1876–1880)Owens College (kini Universitas Manchester) (1863–1875)Pembimbing akademikAugustus De MorganTerinspirasiBe...