Евклідів простір
| |||||||||||||||
Read other articles:

Karya seni kelas bayat, dari buku tahunan Locust tahun 1920 East Texas State Normal College Bayat, bayata (laki-laki), bayati (perempuan), atau bahasa sehari-hari mahasiswa baru, [1] adalah seseorang pada tahun pertama di suatu lembaga pendidikan, biasanya sekolah menengah atau di tingkat perguruan tinggi dan universitas, tetapi juga dalam bentuk lembaga pendidikan pasca sekolah menengah lainnya.[2] Referensi ^ Frosh Definition & Meaning. Merriam-Webster. Diakses tanggal A...
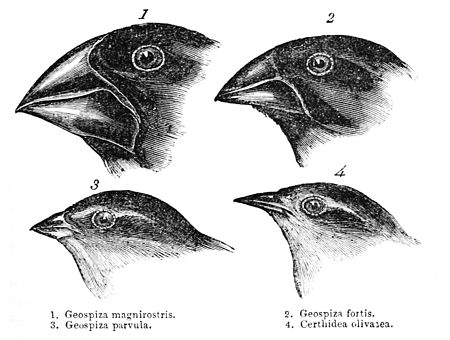
Accumulation of differences between closely related species populations, leading to speciation Darwin's finches are a clear and famous example of divergent evolution, in which an ancestral species radiates into a number of descendant species with both similar and different traits. Part of a series onEvolutionary biologyDarwin's finches by John Gould Index Introduction Main Outline Glossary Evidence History Processes and outcomes Population genetics Variation Diversity Mutation Natural selecti...

Shadow ministry of the Australian opposition from 1972 to 1975This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Shadow Ministry of Billy Snedden – news · newspapers · books · scholar · JSTOR (February 2023) The Shadow Ministry of Billy Snedden was the opposition Liberal shadow ministry of Australia f...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Republik Sosialis Soviet Karelo-Finlandia – berita · surat kabar · buku · cendekiawan · JSTOR Republik Sosialis Soviet Karelo-FinlandiaKarjalais-suomalainen sosialistinen neuvostotasavaltaКарело-Ф...

Real BetisNama lengkapReal Betis BalompiéJulukanBéticos Verdiblancos Berdiri12 September 1907StadionEstadio Benito Villamarín Sevilla, Andalusia, Spanyol(Kapasitas: 56.432)Ketua Ángel HaroManajer Manuel PellegriniLigaLa Liga2022–2023La Liga, ke-6 dari 20Situs webSitus web resmi klub Kostum kandang Kostum tandang Kostum ketiga Musim ini Real Betis Balompié, S.A.D., mengarah ke Betis (diucapkan [ˈβetis]), tim sepak bola profesional yang berbasis di Sevilla. Real Betis Balompi...

Canadian gridiron football player (born 1948) Tony GabrielNo. 77Canada's Sports Hall of Fame Induction, November 10, 2010Born: (1948-12-11) December 11, 1948 (age 75)Burlington, Ontario, CanadaCareer informationCFL statusNationalPosition(s)TEHeight6 ft 4 in (193 cm)Weight210 lb (95 kg)CollegeSyracuseHigh schoolBurlington CentralCareer historyAs player1971–1974Hamilton Tiger-Cats1975–1981Ottawa Rough Riders Career highlights and awards...

Red-tailed hawk living in New York City (1990–2023) This article is about the hawk. For other uses, see Pall Mall. Pale MalePale Male eating a pigeon in 2011SpeciesButeo jamaicensisSexMaleHatched1990 (1990)DiedMay 16, 2023(2023-05-16) (aged 32–33)Long Island, New York, U.S.Nation fromUnited StatesKnown forNesting on 927 Fifth AvenueMate(s) First Love (1992, c. 1995–1997) Chocolate (c. 1992–1995) Blue (1998 – c. September 11, 2001) Lola (2002 – Dece...

Monarchy in Central Asia from 1823 to 1926 Not to be confused with Islamic Emirate of Afghanistan, Islamic Emirate of Afghanistan (1996–2001), or Emirate of Afghanistan (1929). Emirate of AfghanistanEmirate of Kabul (1823–1855)امارت افغانستان (Persian)Imārat-i Afğānistān1823–1926 Flag (1919–1926) Emblem (1919–1926) Map of the Emirate of Afghanistan after the Durand Line AgreementAfghanistan before the 1893 Durand Line AgreementMap of the Emirate of Afghanistan...

United States Marine Corps Color GuardMembers of the USMC Color Guard display the colors during the Friday Evening Parade.Country United StatesBranch USMCTypeColor GuardSize4Part ofColor Guard Platoon, Ceremonial Company A[1]Garrison/HQMarine Barracks WashingtonNickname(s)The Commandant's FourParade FourCommandersColor Sergeant of the Marine CorpsSergeant Stephen A. SextonMilitary unit The United States Marine Corps Color Guard The Commandant's Four is the official col...

Art and LanguageHistoireFondation 1968CadreType Mouvement artistique, collectif d'artistesMouvement Art conceptuel, art contemporainPays Royaume-Uni États-Unis AustralieOrganisationFondateurs Michael Baldwin, David Bainbridge, Terry Atkinson, Harold HurrellSite web art-language.orgmodifier - modifier le code - modifier Wikidata Art and Language est un collectif d'artistes conceptuels britanniques fondé en 1968 à Coventry en Angleterre. Il a eu un rôle essentiel, de même q...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Refugee Week – news · newspapers · books · scholar · JSTOR (November 2008) This article relies ex...

Про Символи, які є математичними знаками див. Таблиця математичних символів. Знаки плюс і мінус використовуються для позначення знака числа. В математиці, поняття знак відноситься до властивості кожного відмінного від нуля дійсного числа бути додатнім або від'ємним. Сам...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Effect of taxes and subsidies on price – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this message) Part of a series onTaxation An aspect of fiscal policy Policies Government revenue Property tax equalization Tax revenue...

Representación gráfica de la ley de Gay-Lussac: a volumen constante V, la presión P es proporcional a la temperatura La ley de Gay-Lussac[1] establece que la presión de un volumen fijo de un gas, es directamente proporcional a su temperatura. Simbología Simbología Símbolo Nombre Unidad k {\displaystyle k} Constante de proporcionalidad Pa / K p {\displaystyle p} Presión Pa p 1 {\displaystyle p_{1}} Presión inicial Pa p 2 {\displaystyle p_{2}} Presión final Pa T {\displaystyle ...

RIM-66 Standard MR A RIM-66 Standard MR pada peluncur Mk-26 Jenis Medium-range surface-to-air missile Negara asal Amerika Serikat Sejarah pemakaian Masa penggunaan 1967 (RIM-66A SM-1MR Block I)1979 (RIM-66C SM-2MR)[1] Digunakan oleh United States Navy, Japanese Maritime Self-Defense Force, Royal Australian Navy, Turkish Navy, Royal Netherlands Navy, German Navy, Royal Canadian Navy, Chilean Navy and Others Sejarah produksi Produsen Raytheon dan lainnya Diproduksi Sejak...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (فبراير 2017) مجلس قضاء ميلة مجلس قضاء ميلة تفاصيل الوكالة الحكومية تأسست ت 12 يوليو 1974&...

American musician, conductor and arranger (1918–2015) This article is about the leader of the Ray Charles Singers. For the rhythm and blues singer, see Ray Charles. Ray CharlesCharles in 1975Background informationBirth nameCharles Raymond OffenbergBorn(1918-09-13)September 13, 1918Chicago, Illinois, U.S.DiedApril 6, 2015(2015-04-06) (aged 96)Beverly Hills, California, U.S.Occupation(s)Musician, singer, songwriter, arranger, conductorInstrument(s)VocalsYears active1942–2015LabelsEssex...

Le Fujian La structure administrative du Fujian, province de la république populaire de Chine (RPC), est constituée des trois niveaux suivants : 9 subdivisions de niveau préfecture ce sont toutes des villes-préfectures 85 subdivisions de niveau district 14 villes-districts 45 xian 26 districts 1111 subdivisions de niveau canton 608 bourgs 334 cantons 18 cantons ethniques 151 sous-districts Les îles de Jinmen (Quemoy) et Matsu sont administrées par la république de Chine à Taïwan...

County in Virginia, United States County in VirginiaAppomattox CountyCountyThe Appomattox County Courthouse in October 2007 FlagLocation within the U.S. state of VirginiaVirginia's location within the U.S.Coordinates: 37°21′32″N 78°49′35″W / 37.358973°N 78.826438°W / 37.358973; -78.826438Country United StatesState VirginiaFounded1845Named forAppomattox RiverSeatAppomattoxLargest townAppomattoxArea • Total335 sq mi (870 k...

Hindu Temple in Uttar Pradesh, India This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sita Samahit Sthal – news · newspapers · books · scholar · JSTOR (September 2019) (Learn how and when to remove this message) Sita Samahit Sthal (Sitamarhi) Templeसीता समाहित स्थल (सीताम...






















