Довірчий інтервал
|
Read other articles:

Yang Berbahagia Tan Sri Dato' Seri PanglimaAbdul Hamid Badorعبد الحميد بن بادور Kepala Kepolisian Kerajaan Malaysia 12Masa jabatan4 Mei 2019 – 3 Mei 2021Penguasa monarkiAbdullah dari PahangPerdana MenteriMahathir MohamadMuhyiddin YassinMenteriMuhyiddin YassinHamzah Zainuddin PendahuluMohammad Fuzi HarunPenggantiAcryl Sani Abdullah SaniWakil Kepala Kepolisian Kerajaan MalaysiaPenjabatMasa jabatan15 Maret 2019 – 4 Mei 2019Penguasa monarkiAbdullah dari P...

Asteroid, disebut juga planet minor atau planetoid, adalah benda berukuran lebih kecil daripada planet, tetapi lebih besar daripada meteoroid, umumnya terdapat di bagian dalam Tata Surya (lebih dalam dari orbit planet Neptunus). Asteroid berbeda dengan komet dari penampakan visualnya. Komet menampakkan koma (ekor) sementara asteroid tidak. Istilah ini secara historis ditujukan untuk semua objek astronomis yang mengelilingi matahari dan setelah diobservasi tidak memiliki karakteristik komet ak...

Sekolah Tinggi Ilmu Hukum Tambun Bungai (selanjutnya disingkat STIH Tambun Bungai atau STIH-TB) merupakan salah satu perguruan tinggi swasta di Kota Palangka Raya, Provinsi Kalimantan Tengah. STIH Tambun Bungai didirikan para tahun 19 Juni 1974 bersamaan dengan pendirian yayasan yang mengelolanya, yaitu Yayasan Pendidikan Tambun Bungai.[1] Kampus STIH Tambun Bungai beralamat di Jalan Sisingamangaraja 35 Palangka Raya.[2] STIH Tambun Bungai mengelola 1 program studi, yaitu Prog...

Heritage registers in Canada NHSC redirects here. For other uses, see NHSC (disambiguation). BC AB SK MB ON QC NB PE NS NL YT NT NU Click on a province/territory for a list of its National Historic Sites National Historic Sites of Canada (French: Lieux historiques nationaux du Canada) are places that have been designated by the federal Minister of the Environment on the advice of the Historic Sites and Monuments Board of Canada (HSMBC), as being of national historic significance.[1]&#...

العلاقات الكندية الليسوتوية كندا ليسوتو كندا ليسوتو تعديل مصدري - تعديل العلاقات الكندية الليسوتوية هي العلاقات الثنائية التي تجمع بين كندا وليسوتو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة كندا ليس...

The Kings have played at Staples Center since 1999. This is a list of seasons completed by the Los Angeles Kings of the National Hockey League. This list documents the records and playoff results for all seasons the Kings have completed in the NHL since their inception in 1967. Table key Key of colors and symbols Color/symbol Explanation † Stanley Cup champions ‡ Conference champions ↑ Division champions # Led league in points Key of terms and abbreviations Term or abbreviation Definit...

Sporting event delegationSweden at the1988 Winter OlympicsIOC codeSWENOCSwedish Olympic CommitteeWebsitewww.sok.se (in Swedish and English)in CalgaryCompetitors67 (54 men, 13 women) in 9 sportsFlag bearer Thomas Wassberg (cross-country skiing)MedalsRanked 5th Gold 4 Silver 0 Bronze 2 Total 6 Winter Olympics appearances (overview)192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022 Sweden competed at the 1988 Winter Olympics in Calgary, Al...

Peta Constantina (2008). Constantina merupakan sebuah kota yang terletak di wilayah Provinsi Sevilla, Andalusia, Spanyol Lihat juga Daftar munisipalitas di Seville Daftar munisipalitas di Spanyol lbsKota di Provinsi Sevilla Aguadulce Alanís Albaida del Aljarafe Alcalá de Guadaíra Alcalá del Río Alcolea del Río Algámitas Almadén de la Plata Almensilla Arahal Aznalcázar Aznalcóllar Badolatosa Benacazón Bollullos de la Mitación Bormujos Brenes Burguillos Camas Cantillana Carmona Carr...

Gugus alkoksi Gugus ariloksi Dalam kimia, gugus alkoksi adalah gugus alkil (rantai karbon dan hidrogen) berikatan tunggal ke oksigen dengan demikian: R–O. Rentang gugus alkoksi sangat besar, yang paling sederhana adalah metoksi (CH3O–). Sebuah gugus etoksi (CH3CH2O–) ditemukan dalam senyawa organik etil fenil eter, C6H5OCH2CH3 yang juga dikenal sebagai etoksibenzena. Terkait dengan gugus alkoksi adalah gugus arikloksi, yang memiliki gugus aril berikatan tunggal dengan oksigen seperti gu...

CfD nomination of Category:Orthopedic surgery Category:Orthopedic surgery has been nominated for renaming. You are encouraged to join the discussion on the Categories for discussion page. Medicine Template‑class Medicine portalThis template is within the scope of WikiProject Medicine. Please visit the project page for details or ask questions at Wikipedia talk:WikiProject Medicine.MedicineWikipedia:WikiProject MedicineTemplate:WikiProject Medicinemedicine articlesTemplateThis template does ...

Bus route in England X5OverviewOperatorFirst West of EnglandGarageWeston-super-MarePeak vehicle requirement3StatusOperatingFormer operator(s)Stagecoach West (2019–2020)RouteStartWeston-super-MareViaWorle, ClevedonEndPortisheadServiceFrequencyevery 60 minutesOperatesMonday to Saturday (except bank holidays)Timetable[1] X5 is a bus route that runs between Weston-super-Mare and Portishead. It is currently operated by First West of England but has been operated by Stagecoach West in the past. H...

Sannakji adalah gurita hidup yang dipotong menjadi potongan-potongan kecil dan disajikan dengan lengan-lengannya yang masih bergerak-gerak. Menyantap hewan hidup adalah praktek manusia menyantap hewan yang masih hidup. Praktek tersebut merupakan praktek tradisional di banyak budaya pangan Asia Timur. Menyantap hewan hidup, atau bagian dari hewan hidup, dianggap ilegal dalam yurisdiksi tertentu di bawah hukum kekejaman hewan. Larangan agama terhadap penyantapan hewan hidup oleh manusia juga mu...

Рафаельітал. Raffaello Sanzio АвтопортретІм'я при народженні Рафаель СантіНародився 28 березня 1483(1483-03-28) Урбіно (область Марке)Помер 6 квітня 1520(1520-04-06) (37 років) Рим·серцева недостатністьПоховання Римський Пантеон[1] і Tomb of RaphaeldКраїна Священна Римська імперіяНаціонал�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dil Ishq – news · newspapers · books · scholar · JSTOR (June 2018) (Learn how and when to remove this message) Pakistani TV series or programme Dil IshqTitle CardGenreSerial dramaRomanceCreated byBabar JavedDeveloped byFaysal ManzoorWritten byAneeza SyedScreenp...

Questa voce sull'argomento cestisti senegalesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Anta SyNazionalità Senegal Altezza183 cm Pallacanestro RuoloAla grande / centro Termine carriera2007 CarrieraSquadre di club 2007CU Dakar Nazionale 1998-2007 Senegal Palmarès Campionati africani ArgentoNigeria 2005 ArgentoSenegal 2007 Il simbolo → indica un trasferimento in prestito. Mod...

Dutch nobleman Portrait of Joan van der Capellen tot den Pol Joan Derk, Baron van der Capellen tot den Pol (Dutch pronunciation: [ˈjoːɑɱ vɑn dər kɑˈpɛlə(n) tɔdəmˈpɔl]; 2 November 1741, Tiel – 6 June 1784, Zwolle) was a Dutch nobleman who played a prominent role in the revolutionary events that preceded the formation of the Batavian Republic. As a member of the Patriots and inspired by the American Revolution, he wrote the noted pamphlet Aan het Volk van Nederland (To t...

У этого термина существуют и другие значения, см. Хойя (значения). Hoya Corporation Тип Публичная компания Листинг на бирже TYO: 7741 Основание 1941 Расположение Токио Ключевые фигуры Хироси Судзуки, Президент и CEO Отрасль производство оптического оборудования и электроники Продукция...

Former design used on United States coinage Draped Bust dollar obverse Draped Bust was the name given to a design of United States coins. It appeared on much of the regular-issue copper and silver United States coinage, 1796–1807.[1][2] It was designed by engraver Robert Scot.[3] Basic design In 1796, Congress responded to the almost universal dissatisfaction of the first coins (Flowing Hair dollar) and decreed a new design. As was the custom of the time, all denomin...
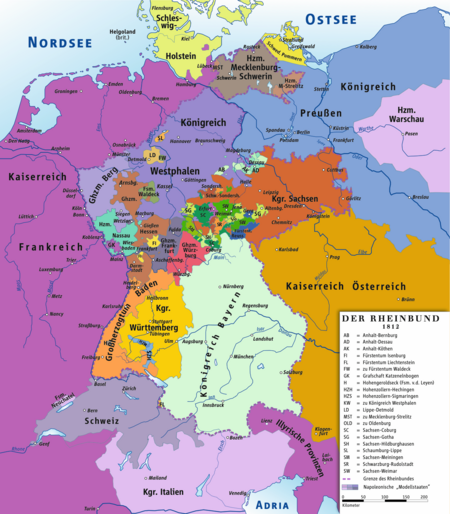
French Revolution The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (July 2022) (Learn how and when to remove this message)The French Revolution had a major impact on Europe and the New World. Historians widely regard the Revolution as one of the most important events in European history.[1][2][3] In the short-term, France lost thousands of its countrymen i...

Robert LewandowskiLewandowski con il Bayern Monaco nel 2019Nazionalità Polonia Altezza185 cm Peso81 kg Calcio RuoloAttaccante Squadra Barcellona CarrieraGiovanili 1996-1997 Partyzant Leszno1997-2004 Varsovia Varsavia Squadre di club1 2004-2005 Delta Varsavia17 (4)2005-2006 Legia Varsavia II13 (2)2006 Znicz Pruszków II4 (8)2006-2008 Znicz Pruszków59 (36)2008-2010 Lech Poznań58 (32)2010-2014 Borussia Dortmund131 (74)2014-2022 Bayern Monaco253 (238)202...






























