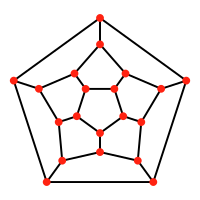
Діаграма Шлегеля
|
Read other articles:

Fantastic GirlsDari kiri ke kanan: Jiyoung, Nicole, Gyuri, Seungyeon and Hara.Album studio karya KaraDirilis28 Agustus 2013 (2013-08-28)Direkam2013GenrePop, dance-popDurasi41:55BahasaJepangLabelUniversal SigmaKronologi Kara Kara Solo Collection(2012)Kara Solo Collection2012 Fantastic Girls(2013) Full Bloom(2013)Full Bloom2013 Singel dalam album Fantastic Girls Bye Bye Happy Days!Dirilis: 27 Maret 2013 Thank You Summer LoveDirilis: 24 Juli 2013 Fantastic Girls adalah album studio berb...

2000 studio album by New York Art Quartet35th ReunionStudio album by New York Art QuartetReleased2000RecordedJune 14, 1999StudioAvatar StudiosGenreFree jazzLabelDIW RecordsProducerVerna GillisNew York Art Quartet chronology Mohawk(1965) 35th Reunion(2000) Old Stuff(2010) 35th Reunion is the third album by the New York Art Quartet. It was recorded at Avatar Studios in New York City on June 14, 1999, and was released in 2000 by DIW Records. It features John Tchicai on alto saxophone, Ro...

Halaman ini berisi artikel tentang pemeran Amerika Serikat. Untuk petinju Australia, lihat Brad Pitt (petinju). Brad PittBrad Pitt - Hollywood California - July 2019LahirWilliam Bradley Pitt18 Desember 1963 (umur 60)Shawnee, Oklahoma, Amerika SerikatKebangsaanAmerika SerikatAlmamaterKickapoo High SchoolUniversitas MissouriPekerjaanPemeran • produser dengan Plan B EntertainmentTahun aktif1987–sekarangKaryaFilmografiKota asalSpringfield, Missouri, ASKekayaan bersih$240 j...

The Man Who Knew InfinityTheatrical release posterSutradaraMatthew BrownProduserEdward R. PressmanJim YoungJoe ThomasMark MontgomerySkenarioMatthew BrownBerdasarkanThe Man Who Knew Infinityoleh Robert KanigelPemeranDev PatelJeremy IronsDevika BhiseToby JonesStephen FryJeremy NorthamKevin McNallyEnzo CilentiPenata musikCoby BrownSinematograferLarry SmithPenyuntingJC BondPerusahaanproduksiPressman FilmXeitgeist Entertainment GroupCayenne Pepper ProductionsDistributorWarner Bros.(Inggrisbr...

Subdistrict of Tallinn, Estonia This article is about the subdistrict in Nõmme District, Tallinn. For the village in Saku Parish, see Männiku, Saku Parish. You can help expand this article with text translated from the corresponding article in Estonian. (July 2010) Click [show] for important translation instructions. View a machine-translated version of the Estonian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translator...

Pengunjuk rasa di Dar es Salaam menentang Perang Gaza 2009 Israel Geografi Tanah Israel DistrikKotaTransportasi Laut MerahLaut Tengah Danau GalileaLaut Mati YerusalemTel AvivHaifa Sejarah Sejarah Yahudi (garis waktu) ZionismeAliyahTheodor Herzl Deklarasi BalfourMandat Palestina Rencana Pembagian Palestina Deklarasi Pengetatan anggaran Konflik Konflik Arab–IsraelKonflik Israel–PalestinaKonflik proksi Iran–Israel Perang 1948Gencatan Senjata 1949 Perjanjian damai dengan Mesirdengan Yordani...

У этого термина существуют и другие значения, см. Верба (значения). БМ-21У «Верба» Классификация реактивная система залпового огня Шасси КрАЗ-6322–010[1][2] История Страна-разработчик Украина Годы производства с декабря 2015 Количество выпущенных 113[3] шт. Разме...

Pour les articles homonymes, voir Le Docteur Jivago. Cet article possède un paronyme, voir Dr. Z-Vago. Le Docteur Jivago Omar Sharif et Julie Christie dans une scène du film. Données clés Titre original Doctor Zhivago Réalisation David Lean Scénario Robert Bolt Musique Maurice Jarre Acteurs principaux Omar SharifJulie ChristieAlec Guinness Sociétés de production Metro-Goldwyn-Mayer Pays de production Royaume-Uni États-Unis Italie Genre drame, romance, historique Durée 201 minu...

French actress (born 1932) Marthe VillalongaMarthe Villalonga at the Cannes Film FestivalBornMarthe Sylvia Gilda Marie Thérèse Villalonga (1932-03-20) 20 March 1932 (age 92)Bordj El Kiffan, AlgeriaOccupation(s)Actress, ComedianYears active1958–present Marthe Villalonga (born 20 March 1932) is a French actress. She was born in Fort-de-l'Eau, Algeria. Theatre Year Title Author Director Notes 1958-60 La Famille Hernandez Geneviève Baïlac Geneviève Baïlac Théâtre du Gymnase Ma...

1999 single by DMX What's My Name?Single by DMXfrom the album ...And Then There Was X ReleasedDecember 28, 1999Recorded1999GenreHardcore hip hopgangsta rapLength3:52LabelRuff RydersDef JamSongwriter(s)Earl SimmonsProducer(s)Self Edward HinsonIrv GottiDMX singles chronology No Love 4 Me (1999) What's My Name? (1999) Party Up (Up In Here) (2000) What's My Name? is a song by American hip hop recording artist DMX, released as the first single released from his third album ...And Then There Wa...

Airline alliance Vanilla AllianceLaunch date21 September 2015; 8 years ago (2015-09-21)Full members5Destination airports89Destination countries26Annual passengers (M)2.3[1]Fleet size46ManagementMarie-Joseph Malé, president[2] The Vanilla Alliance (French: Alliance Vanille) is an airline alliance formed in September 2015. The alliance is the fourth largest in the world as of 2018, trailing Oneworld, Star Alliance, and SkyTeam.[3] All of the airlines w...

This article may be too long to read and navigate comfortably. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (August 2023) Part of a series on the History of Austria Early history Hallstatt culture Noricum - Pannonia - Raetia Marcomanni - Lombards - Bavarians - Suebi Avars Samo's Realm Carantania East Francia Duchy of Bavaria - Margraviate of Austria House of Babenberg Privilegium Minus Habsburg era H...

Japan Open Tennis Championships 1973Singolare Sport Tennis Vincitore Ilie Năstase Tom Okker Finalista Antonio Muñoz Manuel Orantes Punteggio 4-6, 6-3, 6-2 Tornei Singolare Singolare Doppio Doppio 1974 Voce principale: Japan Open Tennis Championships 1973. Ilie Năstase e Tom Okker hanno battuto in finale Antonio Muñoz e Manuel Orantes 4-6, 6-3, 6-2. Indice 1 Teste di serie 2 Tabellone 2.1 Legenda 2.2 Finale 2.3 Parte alta 2.4 Parte bassa 3 Collegamenti esterni Teste di serie Pierre...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Masjid Jami' Cipari adalah salah satu masjid tertua di Kabupaten Garut, Provinsi Jawa Barat, Indonesia. Masjid yang berlokasi di Kampung Cipari, Desa Sukarasa, Kecamatan Pangatikan, Kabupaten Garut ini mulai dibangun tahun 1895 dalam kompleks pesantren dan baru selesai pada tahun 1934.[1] Pendirinya adalah K.H. Yusuf Taudziri.[2] Arsitektur Masjid ini memiliki keunikan karena mirip dengan bangunan gereja. Ciri yang menegaskan bahwa bangunan tersebut adalah masjid, hanyalah kub...

لمعانٍ أخرى، طالع بينيت (توضيح). بينيت الإحداثيات 40°40′49″N 96°30′23″W / 40.680277777778°N 96.506388888889°W / 40.680277777778; -96.506388888889 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة لانكستر خصائص جغرافية المساحة 1.315714 كيلومتر مربع1...

299-та бригада тактичної авіації(з 2003) 299-й окремий штурмовий авіаційний полк(1994—2003) 299-й корабельний штурмовий авіаційний полк(1992—1994) Нарукавний знак бригадиНа службі 1992—дотеперКраїни УкраїнаВид Повітряні силиз 1996 Військово-морські сили1992—1996Тип Тактична авіа...

American politician (born 1986) Lauren BoebertOfficial portrait, 2020Member of the U.S. House of Representativesfrom Colorado's 3rd districtIncumbentAssumed office January 3, 2021Preceded byScott Tipton Personal detailsBornLauren Opal Roberts (1986-12-19) December 19, 1986 (age 37)Altamonte Springs, Florida, U.S.Political partyRepublican (since 2008)Other politicalaffiliationsDemocratic (2006–2008)Spouse Jayson Boebert (m. 2007; div.&...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. Amy YamazakiLahir1991PekerjaanPemeranTahun aktif2001–2012 Amy Yamazaki adalah seorang pemeran berkebangsaan Britania Raya. Ia dikenal karena perannya sebagai Charlotte Lau dalam sinetron long-running Channel 4 Hollyoaks.[1] Referensi ^ Onl...

Politics of Zambia Constitution Human rights Government President Hakainde Hichilema Vice-President Mutale Nalumango Cabinet Legislature National Assembly Speaker: Nelly Mutti Constituencies Judiciary Constitutional Court President: Mulela Margaret Munalula Supreme Court Chief Justice: Mumba Malila Elections General 1964 1968 1973 1978 1983 1988 1991 1996 2001 2006 2011 2016 2021 Presidential 2008 2015 Referendums 1969 2016 Political parties By-elections Administrative divisions Provinces Di...