Figurate number
|
Read other articles:

Frederick Cornwallis ConybeareLahir14 September 1856Coulsdon, SurreyMeninggal9 Januari 1924(1924-01-09) (umur 67)PekerjaanOrientalist, teolog, penulis Frederick Cornwallis Conybeare, FBA (14 September 1856 – 9 Januari 1924) adalah seorang orientalis Inggris, Fellow dari University College, Oxford, dan Profesor Teologi di Universitas Oxford. Biography Conybeare lahir di Croydon, Surrey, anak ketiga dari seorang pengacara, John Charles Conybeare, dan cucu dari ahli geolog...

لمعانٍ أخرى، طالع رافينا (توضيح). رافينا الإحداثيات 42°28′35″N 73°48′51″W / 42.476388888889°N 73.814166666667°W / 42.476388888889; -73.814166666667 [1] تاريخ التأسيس 1914 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ألباني خصائص جغرافية المساحة 3...

A questa voce o sezione va aggiunto il template sinottico {{Militare}} Puoi aggiungere e riempire il template secondo le istruzioni e poi rimuovere questo avviso. Se non sei in grado di riempirlo in buona parte, non fare nulla; non inserire template vuoti. Questa voce o sezione sugli argomenti nobili e politici albanesi non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Voce in gran parte priva di fonti e note a supporto. Puoi migliorare que...

Mahkamah Agung Uni Soviet (bahasa Rusia: Верховный Суд СССР, Verkhovnyi Sud SSSR) merupakan mahkamah agung di Uni Soviet. Mahkamah ini terdiri atas Kolegium Militer dan unsur-unsur lain yang jarang ditemukan dalam susunan mahkamah agung di negara lain, baik pada masa lalu maupun sekarang. Lihat pula Kementerian Hukum Uni Soviet Pengadilan Negeri Uni Soviet Jaksa Agung Uni Soviet lbsTopik mengenai Uni SovietSejarah Periodisasi Revolusi Rusia (Februari dan Oktober 1917) Pera...

2007 Malaysian filmFlower in the PocketDirected byLiew Seng TatWritten byLiew Seng TatProduced byYen San Michelle LoStarringWong Zi JiangLim Ming WeiAmira Nasuha ShahiranJames LeeAzman Md. HasanCinematographyAlbert Hue See LeongRelease date 2007 (2007) Running time97 minutesCountryMalaysiaLanguagesMandarinCantoneseMalayBudgetRM 64,000Box officeRM 11,000 Flower In The Pocket (Chinese: 口袋裏的花) is a 2007 Malaysian independent film written and directed by Liew Seng Tat. The fil...

Shenzhen Open 2015 Sport Tennis Data 3 gennaio - 10 gennaio Edizione 3ª Superficie Cemento Montepremi 500 000 $ Campioni Singolare Simona Halep Doppio Ljudmyla Kičenok / Nadežda Kičenok 2014 2016 Lo Shenzhen Open 2015 è un torneo di tennis giocato all'aperto sul cemento. È la 3ª edizione dello Shenzhen Open, che fa parte della categoria International nell'ambito del WTA Tour 2015. Si gioca allo Shenzhen Longgang Tennis Centre di Shenzhen in Cina, dal 3 al 10 gennaio 2015. In...

Ancient tribe in southern Albania This article is about the ancient tribe in modern southern Albania. For the northern Illyrian tribe, see Amantini. A bronze coin bearing with the heads of Zeus and Dione on the obverse (left) and the legend ΑΜΑΝΤΩΝ (AMANTON) and a serpent on the reverse (right). The Amantes (alternatively attested in primary sources, as Amantieis or Amantini) (Ancient Greek: Άμαντες or Αμαντιείς; Latin: Amantinii) were an ancient tribe located in the in...

John Gray John Gray (Brooklyn, ...) è un regista, sceneggiatore e produttore televisivo statunitense. Indice 1 Biografia 2 Filmografia 2.1 Regista 2.2 Sceneggiatore 2.3 Produttore 3 Collegamenti esterni Biografia Ha iniziato la carriera nel 1982 come regista del serial Power House, sospesa dopo otto episodi, con interprete Henry Winkler. È conosciuto per essere l'ideatore della serie televisiva prodotta dalla CBS Ghost Whisperer - Presenze, in onda negli Stati Uniti fra il 2005 e il 2010, c...

Attentato del mercato di NetanyaattentatoTipoattacco suicida Data19 maggio 2002 LuogoNetanya, Israele Stato Israele Coordinate32°19′46.19″N 34°51′34.6″E / 32.329496°N 34.859612°E32.329496; 34.859612Coordinate: 32°19′46.19″N 34°51′34.6″E / 32.329496°N 34.859612°E32.329496; 34.859612 ResponsabiliHamas e il Fronte Popolare per la Liberazione della Palestina rivendicarono l'attentato ConseguenzeMorti3 (e un attentatore suicida) Feriti56...

Smartphones manufactured by Xiaomi Xiaomi Mi 5cCodenamemeriManufacturerXiaomiSeriesMiFirst releasedMarch 2017PredecessorXiaomi Mi 4cRelatedXiaomi Mi 4cTypeSmartphoneForm factorSlate phoneDimensions144.38 x 69.68 x 7.09 mmMass135 gOperating systemMIUI 8 (Android 6.0)System-on-chipXiaoMi pinecone S1CPU2x Dual-core 2.2GHz + 2x Dual-core 1.4GHzGPUMali-T860 2x Dual-coreMemory3 GB RAMStorage64 GB EMMC 5.0BatteryNon-removable Li-Po 2860mAh(typ) / 2810mAh(min) batteryDisplay5.15 1920*1080 pix...

Sputnik 1 La nave Sputnik 1Tipo de misión Estudios astronómicosOperador Unión SoviéticaID COSPAR 1957-001Bno. SATCAT 00002ID NSSDCA 1957-001BPágina web [1 enlace]Duración de la misión 3 mesesÓrbitas completadas 1440Propiedades de la naveFabricante Serguéi KoroliovMasa de lanzamiento 83,6 kgComienzo de la misiónLanzamiento 4 de octubre de 1957 a las 19:12 UTCVehículo R-7/SS-6 ICBMLugar Plataforma GagarinFin de la misiónTipo Pérdida de señalÚltimo contacto 1957-10-26Parámetros o...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Pabrik Pelumas ChonjiJosŏn-gŭl천지윤활유공장 Alih AksaraCheonji Yunhwalyu GongjangMcCune–ReischauerCh'ŏnji Yunhwalyu Kongjang Pabrik Pelumas Ch'ŏnji, yang terletak di Hanggu-guyŏk, Namp'o, Korea Utara, adalah sebuah pabrik yang memproduk...

Ballon d'Or 2008Pemenang Ballon d'Or 2008 Cristiano RonaldoTanggal2 Desember 2008 (2008-12-02)LokasiParis, PrancisNegaraPrancisDipersembahkan olehFrance FootballIkhtisarDimenangkan oleh Cristiano Ronaldo (gelar pertama)Situs webwww.francefootball.fr← 2007 Ballon d'Or2009 → Ballon d'Or 2008, yang diberikan kepada pemain sepak bola terbaik di dunia menurut penilaian panel jurnalis olahraga internasional,[1] dianugerahkan pada tanggal 2 Desember.[2] Cristiano Ro...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Pemandangan persimpangan State Road 3 dan US 224 di Markle Markle adalah sebuah kota di kabupaten Huntington dan Wells, di negara bagian Indiana, AS.[1] Populasi adalah 1.071 pada sensus 2020. Itu terletak di sepanjang Interstate 69, US Route 2...
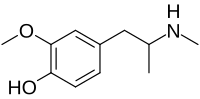
4-Hydroxy-3-methoxymethamphetamine Names Preferred IUPAC name 2-Methoxy-4-[2-(methylamino)propyl]phenol Identifiers CAS Number 117652-28-5 Y 3D model (JSmol) Interactive image ChemSpider 2338803 PubChem CID 3081137 UNII RBY3J6H4JW Y CompTox Dashboard (EPA) DTXSID70922503 InChI InChI=1S/C11H17NO2/c1-8(12-2)6-9-4-5-10(13)11(7-9)14-3/h4-5,7-8,12-13H,6H2,1-3H3Key: UVDWYWYWOMOEFX-UHFFFAOYSA-N SMILES CC(CC1=CC(=C(C=C1)O)OC)NC Properties Chemical formula C11H17NO2 Molar mass 195.262&...

Campionato mondiale di Formula 1 1998Edizione n. 49 del Campionato mondiale di Formula 1 Dati generaliInizio8 marzo Termine1º novembre Prove16 Titoli in palioPiloti Mika Häkkinensu McLaren MP4/13 Costruttori McLaren Altre edizioniPrecedente - Successiva Edizione in corso Il campionato mondiale di Formula 1 1998 organizzato dalla FIA è stata, nella storia della categoria, la 49ª ad assegnare il Campionato Piloti, vinto per la prima volta dal finlandese Mika Häkkinen, e la 41ª ad asse...

Gambaran Unicorn Merah Muda yang Tak Tampak. Unicorn Merah Muda yang Tak Tampak (bahasa Inggris: Invisible Pink Unicorn, disingkat IPU) adalah sosok dewi dalam agama parodi yang menyindir teisme. Sosok ini merupakan unicorn yang tak tampak, tetapi berwarna merah muda.[1] Ia merupakan gambaran retoris yang disandingkan dengan Monster Spageti Terbang.[2] Sejarah Referensi pertama mengenai Unicorn Merah Muda yang Tak Tampak tertanggal pada 7 Juli 1990[3] dalam perbinc...

Muhammad Saleh Sultan Zainal Abidin Syekh Al Wasil SyamsudinTuanku Tambusai Nama lainDe Padrische Tijger van Rokan atau Harimau Paderi dari RokanInformasi pribadiLahir5 November 1784Dalu-Dalu, Kerajaan Tambusai (sekarang Riau)Meninggal12 November 1882 (umur 98)Seremban, Negeri SembilanAgamaIslamEtnisMinangkabau 'Tuanku Tambusai' (5 November 1784 – 12 November 1882) adalah salah seorang tokoh Paderi terkemuka. Latar belakang Tuanku Tambusai lahir di Daludalu, sebuah desa yang b...

Alebrijes de OaxacaCalcio Los Alebrijes Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori sociali arancio-nero Dati societariCittàOaxaca de Juárez NazioneMessico ConfederazioneCONCACAF Federazione FMF CampionatoLiga de Expansión MX Fondazione2012 ProprietarioJuan Carlos Jones Allenatore Alejandro Pérez StadioEstadio Tecnológico de Oaxaca(14.598 posti) Sito webwww.alebrijesfc.com PalmarèsSi invita a seguire il modello di voce L'Alebrijes de Oaxaca Fútbol Club è un...

American politician This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jim Jontz – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this message) Jim JontzMember of the U.S. House of Representativesfrom Indiana's 5th districtIn officeJanuary 3, 1987 – J...









