Multiply perfect number
|
Read other articles:

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...

Ancient Egyptian funerary text of the New Kingdom of Egypt The Litany of Re (or more fully Book of Praying to Re in the West, Praying to the United One in the West) is an important ancient Egyptian funerary text of the New Kingdom.[1] Like many funerary texts, it was written on the inside of the tomb for reference by the deceased. Unlike other funerary texts, however, it was reserved only for pharaohs or very favored nobility. It is a two-part composition that in the first part invoke...

Nördlingen Nördlingen, south view from the church tower DanielLetak Nördlingen di Donau-Ries NegaraJermanNegara bagianBayernWilayahSchwabenKreisDonau-RiesPemerintahan • Lord MayorHermann Faul (PWG)Luas • Total68,10 km2 (2,630 sq mi)Ketinggian441 m (1,447 ft)Populasi (2013-12-31)[1] • Total19.419 • Kepadatan2,9/km2 (7,4/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos86720Kode area telepon09081Pelat kenda...

العلاقات الإماراتية الصربية الإمارات العربية المتحدة صربيا الإمارات العربية المتحدة صربيا تعديل مصدري - تعديل العلاقات الإماراتية الصربية هي العلاقات الثنائية التي تجمع بين الإمارات العربية المتحدة وصربيا.[1][2][3][4][5] مقارنة بين البل...

State park In Colorado, United States Fishers Peak State ParkFishers Peak in Fishers Peak State ParkThe park's location in ColoradoShow map of ColoradoFishers Peak State Park (the United States)Show map of the United StatesLocationLas Animas County, Colorado, USANearest cityTrinidad, ColoradoCoordinates37°05′52″N 104°27′46″W / 37.09778°N 104.46278°W / 37.09778; -104.46278Area19,200 acres (7,800 ha)[1]Established2020Visitors224 (in ...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (April 2020) 1980 video gameGalactic TraderApple II coverDeveloper(s)CybernauticsRelease1980 Galactic Trader is a 1980 video game published by Cybernautics. Contents Galactic Trader is a game in which the player was a general during the war, but now only commands a small ship that trades goods across the galaxy.[1] Reception Gle...

Provincial park in southern Manitoba Birds Hill Provincial ParkIUCN category III (natural monument or feature)Birds Hill Park, overlooking lakeLocationManitoba, CanadaNearest cityWinnipeg, ManitobaCoordinates50°01′28″N 96°53′01″W / 50.02444°N 96.88361°W / 50.02444; -96.88361Area35.1 km2 (13.6 sq mi)DesignationProvincial ParkEstablished1964Governing bodyGovernment of Manitoba Birds Hill Provincial Park Birds Hill Provincial Park is a...

Pemandangan kota Vaughan Vaughan merupakan sebuah kota di Kanada. Kota ini letaknya di bagian selatan. Tepatnya di negara bagian Ontario. Pada tahun 2006, kota ini memiliki jumlah penduduk sebesar 238.866 jiwa dan memiliki luas wilayah 273,58 km². Kota ini memiliki angka kepadatan penduduk sebesar 873,1 jiwa/km². Pranala luar Wikimedia Commons memiliki media mengenai Vaughan. Situs resmi Artikel bertopik geografi atau tempat Kanada ini adalah sebuah rintisan. Anda dapat membantu Wikipe...

Artikel ini memuat Islam di Israel. Untuk Islam di teritorial Palestina, lihat Islam di Negara Palestina. Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Nig...

Koordinat: 39°59′23″N 116°18′19″E / 39.98972°N 116.30528°E / 39.98972; 116.30528 Universitas Peking北京大学Nama sebelumnyaUniversitas Kapital ImperialJenisNasionalDidirikan1898PresidenZhou Qifeng (周其凤)Staf akademik4.206Sarjana15.128Magister15.039Lokasi Beijing, Republik Rakyat TiongkokKampusUrban, 273 ha (2.73 km2 )Nama julukan北大, BěidàAfiliasiIARU, AEARU, APRU, BESETOHA, C9Situs webwww.pku.edu.cn Universitas Peking (Hanzi sederhana: 北...

Cet article concerne la langue kighize. Pour le peuple kirghiz, voir Kirghizes. Kirghizeкыргыз тили, кыргызчаقىرعىزچا, قىرعىز تىلى Pays Kirghizistan, Tadjikistan, Chine, Afghanistan, Russie Nombre de locuteurs 4 331 020[1] Typologie SOV, agglutinante, accusative, à accent d'intensité Classification par famille - langues turciques - langues kiptchak - groupe kiptchak méridional (aralo-caspien) - kirghiz Statut officiel Langue officielle Kir...

Some rose growers are known for their particular contributions to the field. These include: A David C.H. Austin (1926–2018), British breeder of English-style roses including the 'Wife of Bath' B Henry Bennett (1823–1890) René Barbier (1870–1931), of Barbier Frères & Compagnie, an early twentieth-century French company based near Orléans (France), produced some very popular Ramblers including 'Albéric Barbier' (1900), 'Paul Transom' (1901), 'Alexandre Girault' (1909), and 'Alber...

Proud of You MoslemLagu oleh Fatin Shidqiadari album 12 Lagu Islami Terbaik - Fatin & FriendsDirilis18 Juni 2014 (2014-06-18)FormatDigital downloadDirekam2014GenrePopDurasi3:44LabelSony Music Entertainment IndonesiaPenciptaAde GovindaProduserAde GovindaVideo musikProud of You Moslem di YouTube Proud of You Moslem adalah lagu dari penyanyi Fatin Shidqia. Lagu ini merupakan single religi yang dirilis untuk menyambut bulan suci Ramadhan dan terdapat di dalam album kompilasi Fatin bersam...

1987 TV series or program Hoover vs. The KennedysGenreHistorical dramaWritten byMichael O'HerlihyLionel E. SiegeNo. of episodes4ProductionProducersPaul SaltzmanDaniel SelznickJoe GlickmanProduction locationsToronto, OntarioProduction companyOperation Prime TimeOriginal releaseRelease1987 (1987) Hoover vs. The Kennedys: The Second Civil War is a four-hour 1987 made-for-television mini-series depicting the political struggles between FBI Director J. Edgar Hoover and President John F. Kenne...

لمعانٍ أخرى، طالع جون وايت (توضيح). هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2019) جون وايت معلومات شخصية الميلاد 2 مارس 1855 الجنسية المملكة المتحدة الحياة العملية المهنة لاعب كريكت، وعاز�...

Knoxville Challenger 2011Sport Tennis Data8 novembre - 13 novembre Edizione8ª LocalitàKnoxville, USA CampioniSingolare Jesse Levine Doppio Steve Johnson / Austin Krajicek 2010 2012 Il Knoxville Challenger 2011 è stato un torneo professionistico di tennis maschile giocato sul cemento. È stata l'8ª edizione del torneo, facente parte dell'ATP Challenger Tour nell'ambito dell'ATP Challenger Tour 2011. Si è giocato a Knoxville nrgli USA dall'8 al 13 novembre 2011. Indice 1 Partecipanti 1.1 T...

2015–2016 student movement in South Africa The correct title of this article is #FeesMustFall. The omission of the # is due to technical restrictions. #FeesMustFallA group of students raise their hands in the air to signal that they have come in peace.Date12 October 2015 – October 2016LocationSouth Africa[1]Caused byAn increase in fees by South African universitiesMethodsProtestResulted in No university fee increases in 2016 Over R 800 million in property damage[2] (roughl...

Universal Studios theme park in Singapore Universal Studios SingaporeUniversal Studios Singapore entranceLocationResorts World, Sentosa, SingaporeCoordinates1°15′14″N 103°49′26″E / 1.254°N 103.824°E / 1.254; 103.824StatusOperatingOpened18 March 2010; 14 years ago (2010-03-18) (soft opening)28 May 2011; 13 years ago (2011-05-28) (grand opening)OwnerGenting Singapore (under a license from NBCUniversal)Operated byGenting Sin...

هذه المقالة عن التاريخ الحديث للمدينة. لالتاريخ القديم لها، طالع الرها. أورفة الرها صورة لجامع في المدينة تقسيم إداري البلد تركيا[1] عاصمة لـ محافظة أورفة المنطقة جنوب شرق الأناضول المحافظة شانلي أورفا المسؤولون العمدة جلال الدين غوفانتش خصائص جغرافية إح�...
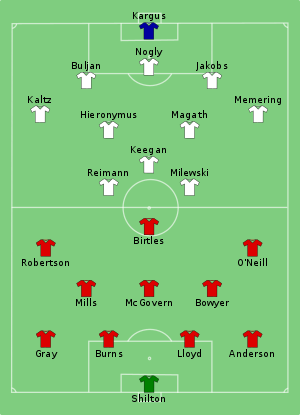
Cet article est une ébauche concernant une rencontre de football et l’Europe. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Finale de la Coupe des clubs champions européens 1979-1980 Le stade Santiago Bernabéu, hôte de la finale. Contexte Compétition Coupe des clubs champions 1979-1980 Date 28 mai 1980 Stade Santiago Bernabéu Lieu Madrid, Espagne Affluence 51 000 spectateurs Résultat Nottingham F...








![{\displaystyle r\left({\sqrt[{r}]{3/2}}-1\right)<\sum _{i=1}^{r}{\frac {1}{p_{i}}}<r\left(1-{\sqrt[{r}]{6/k^{2}}}\right),~~{\text{if }}n{\text{ is even}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/413cf0a0d2e58457c15f88760e2022db99e6660c)
![{\displaystyle r\left({\sqrt[{3r}]{k^{2}}}-1\right)<\sum _{i=1}^{r}{\frac {1}{p_{i}}}<r\left(1-{\sqrt[{r}]{8/(k\pi ^{2})}}\right),~~{\text{if }}n{\text{ is odd}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a14ab363496c148721680c431a26a3db3dfc267a)
