Lazy caterer's sequence
|
Read other articles:

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Yarrow mamout nama lain Mahmoud (Muhammad) Yaro atau Mamadao Yarrow (lahir 1736-1823) adalah mantan budak muslim yang dibebaskan, usahawan, pemilik properti di Georgetown dan investor Columbia bank Amerika.[1][2][3] Lukisan Yarrow M...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) فرناندو كاسترو باتشيكو معلومات شخصية الميلاد 26 يناير 1918 ماردة الوفاة 8 أغسطس 2013 (95 سنة) [1] ماردة مواطنة المكسيك الحياة العملية المهنة ...

Final Piala Dunia FIFA 2014Timnas Jerman mengangkat trofi Piala Dunia.TurnamenPiala Dunia FIFA 2014 Jerman Argentina 1 0 setelah perpanjangan waktuTanggal13 Juli 2014StadionStadion Maracanã, Rio de JaneiroPemain Terbaik Mario Götze (Jerman)WasitNicola Rizzoli (Italia)Penonton74.738CuacaSebagian berawan23 °C (73 °F)kelembapan 65%[1]← 2010 2018 → Final Piala Dunia FIFA 2014 adalah pertandingan sepak bola yang berlangsung pada 13 Juli 2014 (tanggal 14 Juli 2014,...

Reform synagogue in New Orleans, Louisiana, United States Touro SynagogueTouro Synagogue building, in 2006ReligionAffiliationReform JudaismEcclesiastical or organisational statusSynagogueLeadershipRabbi Katie BaumanRabbi Todd SilvermanRabbi David Goldstein (Emeritus)StatusActiveLocationLocation4238 St. Charles Avenue in Uptown New Orleans, Louisiana 70115CountryUnited StatesLocation in New Orleans, LouisianaGeographic coordinates29°55′34″N 90°06′02″W / 29.926188°N 9...

Popular Buddhist temple in Bagan, Myanmar Sulamani Temple Sulamani Temple Sulamani Temple fresco detail Sulamani Temple fresco The Sulamani Temple (Burmese: စူဠာမဏိဘုရား, pronounced [sùlàmənḭ pʰəjá]) is a Buddhist temple located in the village of Minnanthu (southwest of Bagan) in Myanmar. The temple is one of the most-frequently visited in Bagan. It was built in 1183 by King Narapatisithu,[1]: 178 and is similar to the Thatbyinn...

Plant that has adapted to living in an aquatic environment The flower of Nymphaea alba, a species of water lily Bud of Nelumbo nucifera, an aquatic plant. Aquatic plants are plants that have adapted to living in aquatic environments (saltwater or freshwater). They are also referred to as hydrophytes or macrophytes to distinguish them from algae and other microphytes. A macrophyte is a plant that grows in or near water and is either emergent, submergent, or floating. In lakes and rivers, macro...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Activity where people recreate aspects of a historical event Reenactors in period uniforms firing muskets in the Battle of Waterloo reenactment, in front of the wood of Hougoumont, 2011Historical reenactments (or re-enactment) is an educational or entertainment activity in which mainly amateur hobbyists and history enthusiasts dress in historic uniforms and follow a plan to recreate aspects of a historical event or period. This may be as narrow as a specific moment from a battle, such as the ...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

This article is about the Australian film. For the Oswald the Lucky Rabbit cartoon short, see The Plumber (cartoon). Australian TV series or program The PlumberDVD coverWritten byPeter WeirDirected byPeter WeirStarringJudy MorrisIvar KantsMusic byRory O'DonoghueGerry TollandCountry of originAustraliaOriginal languageEnglishProductionProducerMatt CarrollCinematographyDavid SandersonEditorGerald Turney-SmithRunning time76 minutesOriginal releaseRelease8 June 1979 (1979-06-08) The...

American actor; politician Christopher MitchumMitchum in 2012Born (1943-10-16) October 16, 1943 (age 80)Los Angeles, California, U.S.EducationUniversity of PennsylvaniaTrinity College, DublinUniversity of Arizona, BA in LiteratureOccupationsActorscreenwriterbusinessmanYears active1966–presentPolitical partyRepublicanSpouse Cynthia Cindy Davis (m. 1964; div. 1996)Children4, including Bentley MitchumParentRobert Mitchum (father)Rel...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: SMA Negeri 8 Semarang – berita · surat kabar · buku · cendekiawan · JSTOR (Januari 2024)SMA Negeri 8 SemarangInformasiDidirikan3 September 1979AkreditasiA (Unggul)[1]Nomor Statistik Sekolah30103630100...

32°54′05″N 48°43′52″E / 32.9014°N 48.7311°E / 32.9014; 48.7311 دز نهر دز وهو يمر من وسط مدينة دزفول المنطقة البلد إيران الخصائص الطول 400 كم (249 ميل) المجرى المصب نهر كارون تعديل مصدري - تعديل نهر دز هو أحد أنهار إيران. يتدفق هذا النهر من جبال زاغروس في مدينة أليغودرز في محافظة...

Washington Metro station West Falls ChurchVTThe center track of West Falls Church station, used for train storageGeneral informationLocationIdylwood, Virginia, U.S.Coordinates38°54′03″N 77°11′20″W / 38.9007928°N 77.1889651°W / 38.9007928; -77.1889651Owned byWashington Metropolitan Area Transit AuthorityPlatforms2 island platformsTracks3Connections Metrobus: 28A Fairfax Connector: 703 Loudoun County Transit MegabusConstructionStructure typeAt-grad...

Grand Prix Inggris 2021Detail lombaLomba ke 12 dari 18Grand Prix Sepeda Motor musim 2021Tanggal29 Agustus 2021Nama resmiMonster Energy British Grand PrixLokasiSilverstone CircuitSilverstone, Britania RayaSirkuitFasilitas balapan permanen5.900 km (3.700 mi)MotoGPPole positionPembalap Pol Espargaró HondaCatatan waktu 1:58.889 Putaran tercepatPembalap Fabio Quartararo YamahaCatatan waktu 2:00.098 di lap 6 PodiumPertama Fabio Quartararo YamahaKedua Álex Rins SuzukiKetiga A...

Monthly arts magazine founded in England For the Egyptian magazine, see Apollo (journal). ApolloApollo magazine October 2010 coverEditorEdward BehrensFormer editorsThomas MarksCategoriesFine artsFrequencyMonthly (double issue for July/August)Founded1925CompanyPress HoldingsCountryEnglandBased inLondonLanguageEnglishWebsitewww.apollo-magazine.comISSN0003-6536OCLC1121415135 Apollo is an English-language monthly magazine covering the visual arts of all periods from antiquity to the present day.&...

Paolo BloraNazionalità Italia Motociclismo CarrieraCarriera in SuperbikeEsordio1998 Miglior risultato finale41º Gare disputate39 Punti ottenuti11 Modifica dati su Wikidata · Manuale Paolo Blora (Pavia, 12 ottobre 1969) è un pilota motociclistico italiano, ritiratosi dall'attività agonistica, campione italiano Superbike nel 1998, tecnico della specialità velocità del Gruppo Sportivo Fiamme Oro e responsabile tecnico di numerosi piloti impegnati nel motomondiale[1 ...

Indian social activist and politician (born 1984) Swati MaliwalMaliwal in January 2015Member of Parliament, Rajya SabhaIncumbentAssumed office 19 January 2024Preceded bySushil Kumar GuptaConstituencyDelhiChairperson of Delhi Commission for WomenIn officeJuly 2015 – 19 January 2024 Personal detailsBorn (1984-10-15) 15 October 1984 (age 39)Ghaziabad, Uttar Pradesh, IndiaPolitical partyAAPSpouseNaveen Jaihind (2012-2020)Residence(s)New Delhi, IndiaProfessionPoliticianActivist...
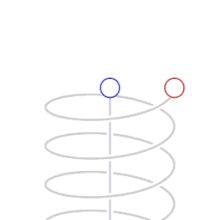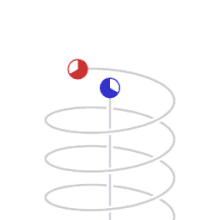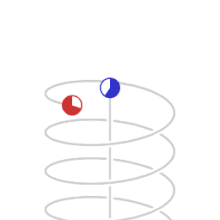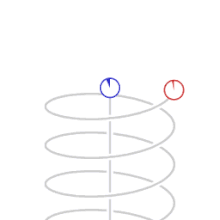
Measured time difference as explained by relativity theory This article is about a physical concept. For the term used in psychology, see Time perception. Special relativity Principle of relativity Theory of relativity Formulations Foundations Einstein's postulates Inertial frame of reference Speed of light Maxwell's equations Lorentz transformation Consequences Time dilation Length contraction Relativistic mass Mass–energy equivalence Relativity of simultaneity Relativistic Doppler effect ...

Former imperial palace in Saint Petersburg, Russia For other uses, see Winter Palace (disambiguation). The Winter Palace, from Palace SquareThe Winter Palace, from Palace EmbankmentThe Winter Palace, from above The Winter Palace[1] is a palace in Saint Petersburg that served as the official residence of the House of Romanov, previous emperors, from 1732 to 1917. The palace and its precincts now house the Hermitage Museum. The floor area is 233,345 square metres (it has been calculated...











