Skewes tal
| |||||||||||||||||||||
Read other articles:

Lucky Buddha BeerBotol Lucky Buddha Beer, menunjukkan bentuk yang khasJenisBirLokasiDanau Qiandao, TiongkokDibukaJuli 2010 Lucky Buddha Beer (Hanzi: 乐开啤酒) adalah bir yang diseduh dan dibotolkan di Danau Qiandao, Tiongkok. Diperkenalkan pada Juli 2010, dan dibuat dari malt, hop, beras, dan air dari wilayah ini, menghasilkan bir bergaya Asia. Rasanya adalah malt bersahaja dengan fitur dari rasa jeruk dengan paduan rasa lemon, jeruk bali, gandum, madu yang digabungkan bersama untuk r...

Julien Féret Informasi pribadiNama lengkap Julien FéretTanggal lahir 5 Juli 1982 (umur 41)Tempat lahir Saint-Brieuc, PrancisTinggi 1,87 m (6 ft 1+1⁄2 in)Posisi bermain GelandangInformasi klubKlub saat ini RennesNomor 8Karier senior*Tahun Tim Tampil (Gol)2000–2003 Rennes B 49 (4)2003–2004 Cherbourg 24 (2)2004–2005 Chamois Niortais 31 (2)2005–2008 Reims 96 (33)2008–2011 Nancy 120 (21)2011– Rennes 31 (8) * Penampilan dan gol di klub senior hanya dihitung ...

Shakira JasmineShakira di tahun 2021Lahir12 Oktober 2002 (umur 21)Cimahi, Jawa Barat, IndonesiaKebangsaanIndonesiaPekerjaanPenyanyiaktrisKarier musikGenrePopInstrumenVokalgitarTahun aktif2013—sekarangLabelMusica Shakira Jasmine (lahir 12 Oktober 2002) adalah seorang penyanyi dan aktris berkebangsaan Indonesia. Shakira merupakan finalis dalam kompetisi The Voice Kids Indonesia musim pertama. Dua tahun pasca lulus dari The Voice Kids Indonesia, ia bergabung dengan perusahaan rekaman Mus...
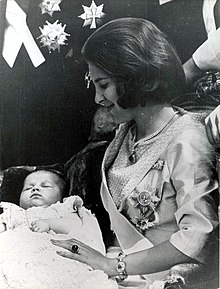
Alessia di GreciaLa principessa Alessia nel 2010Principessa della Corona di GreciaStemma In carica10 luglio 1965 –20 maggio 1967(1 anno e 314 giorni) PredecessoreIrene SuccessorePaolo TrattamentoSua Altezza Reale Altri titoliPrincipessa di Grecia e Danimarca NascitaVilla Mon Repos, Corfù, Regno di Grecia, 10 luglio 1965 (58 anni) DinastiaSchleswig-Holstein-Sonderburg-Glücksburg PadreCostantino II di Grecia MadreAnna Maria di Danimarca ConsorteCarlos Morales Quint...

Ford CityGéographiePays États-UnisÉtat CalifornieComté comté de KernSuperficie 3,97 km2 (2010)Surface en eau 0 %Altitude 272 mCoordonnées 35° 09′ 24″ N, 119° 27′ 29″ ODémographiePopulation 4 348 hab. (2020)Densité 1 095,2 hab./km2 (2020)FonctionnementStatut Localité de recensement aux États-UnisIdentifiantsCode postal 93268Code FIPS 06-24764GNIS 1660645, 2408226Indicatif téléphonique 661modifier - modifier le...

Spanish cardinal In this Spanish name, the first or paternal surname is Rouco and the second or maternal family name is Varela. His EminenceAntonio Rouco VarelaCardinal, Archbishop emeritus of MadridAntonio María Rouco VarelaArchdioceseMadridAppointed28 July 1994Term ended28 August 2014PredecessorAngel Suquía GoicoecheaSuccessorCarlos Osoro SierraOther post(s)Cardinal-Priest of San Lorenzo in DamasoPresident of the Spanish Episcopal ConferenceOrdersOrdination28 March 1959by Ang...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Personal computer by Apple Computer Power Macintosh 6400 / Performa 6400A Macintosh Performa 6400/200.Also known asInstaTower[1]DeveloperApple ComputerProduct familyPower Macintosh, PerformaRelease dateAugust 7, 1996Introductory priceUS$2,400 (equivalent to $4,663 in 2023)DiscontinuedAugust 1, 1997Operating systemSystem 7.5.3 - Mac OS 9.1With PowerPC G3 upgrade, Mac OS 9.2.2CPUPowerPC 603ev @ 180 or 200 MHzMemory16 MB, expandable to 136 MB (70 ns 168-pin DIMM)D...

Ini adalah nama Melayu; nama Ahmad merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Dzulkefly. Yang Berhormat Datuk SeriDzulkefly AhmadDGSM APذوالكفل أحمد Menteri KesehatanPetahanaMulai menjabat 12 Desember 2023Perdana MenteriAnwar IbrahimWakilLukanisman Awang SauniPendahuluZaliha MustafaPenggantiPetahanaDaerah pemilihanKuala SelangorMasa jabatan21 Mei 2018 – 24 Februari 2020Perdana MenteriMahathir MohamadWakilLee Bon Chye...

Major League Baseball team season 1910 Cincinnati RedsLeagueNational LeagueBallparkPalace of the FansCityCincinnatiOwnersGarry HerrmannManagersClark Griffith ← 1909 Seasons 1911 → The 1910 Cincinnati Reds season was a season in American baseball. The Reds finished fifth in the National League with a record of 75–79. Offseason On January 20, the Reds traded pitchers Bob Ewing and Ad Brennan to the Philadelphia Phillies, receiving pitchers Frank Corridon and Harry ...

Restaurant in New York, United StatesAsiateAsiateLocation in ManhattanRestaurant informationEstablished2003; 21 years ago (2003)ChefCyril RenaudFood typeContemporary AmericanStreet addressIn the Mandarin Oriental, New York hotel, on the 35th floor of 80 Columbus Circle (West 60th Street at Broadway), in ManhattanCityNew York CityCountyNew York CountyStateNew YorkPostal/ZIP Code10023CountryUnited StatesCoordinates40°46′05″N 73°58′57″W / 40.767936°N...

Heavy snowstorm that hit Northeast US and Canada in late October that year Halloween nor'easter redirects here. For the 1991 Halloween nor'easter, see 1991 Perfect Storm. 2011 Halloween nor'easterCategory 1 Notable (RSI/NOAA: 1.97)Satellite image of the storm on October 29, 2011 TypeExtratropical cycloneNor'easterBlizzardWinter stormFormedOctober 28, 2011DissipatedNovember 1, 2011(Exited to sea) Lowest pressure971 mb (28.67 inHg) Maximum snowfallor ice ...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. المواد المدورة بعد الاستهلاك (بالإنجليزية: Post-Consumer Materials) هي مخلفات اُستخلصت من المنازل أو المرافق التجارية والصناعية والمؤسسات بحيث أصبح من غير الممكن استخدامها لما صنعت له ...

Star in the constellation Aquila This article is about b Aquilae. It is not to be confused with β Aquilae. 31 Aquilae Location of 31 Aquarii (circled) Observation dataEpoch J2000 Equinox J2000 Constellation Aquila Right ascension 19h 24m 58.20027s[1] Declination +11° 56′ 39.8862″[1] Apparent magnitude (V) 5.16[2] Characteristics Spectral type G8 IV[2] U−B color index +0.42[...

Buja ? Buja (Italien) Staat Italien Region Friaul-Julisch Venetien Koordinaten 46° 13′ N, 13° 8′ O46.21666666666713.133333333333213Koordinaten: 46° 13′ 0″ N, 13° 8′ 0″ O Höhe 213 m s.l.m. Fläche 27,88 km² Einwohner 6.337 (31. Dez. 2022)[1] Postleitzahl 33030 Vorwahl 0432 ISTAT-Nummer 030013 Website Buja Via Tomba, Buja Buja (furlanisch Buje) ist eine Gemeinde mit 6337 Einwohnern (Stand 31. Dezemb...

Andrea Pazienza nel 1974 Andrea Michele Vincenzo Ciro[1] Pazienza (San Benedetto del Tronto, 23 maggio 1956 – Montepulciano, 16 giugno 1988) è stato un fumettista, disegnatore e pittore italiano. Ritenuto uno degli artisti più rappresentativi e innovativi nel campo del fumetto italiano; la sua produzione, incentrata su personaggi come Zanardi e Pentothal, è stata negli anni ristampata più volte e oggetto di mostre e riconoscimenti. Alla sua vita e alle sue opere fu dedicato il f...

1980s Manhattan nightclub 8BC8BC Gallery, exterior view, 1984, from the Archives of American ArtLocationManhattan, New York, U.S.Coordinates40°43′39″N 73°59′09″W / 40.72750°N 73.98583°W / 40.72750; -73.98583OwnerCornelius ConboyDennis GattraTypeNightclub, Art galleryGenre(s)PunkContemporary artOpenedOctober 31, 1983ClosedOctober 22, 1985 8BC was a nightclub, performance space, and art gallery located at 337 East 8th Street in the East Village neighborhood o...

English footballer Jack Beacham Beacham with Brentford in 1926.Personal informationFull name Albert John Beacham[1]Date of birth (1902-08-15)15 August 1902Place of birth Birmingham, EnglandDate of death 14 May 1982(1982-05-14) (aged 79)[2]Place of death Birmingham, EnglandPosition(s) Half backSenior career*Years Team Apps (Gls) Wolseley Motors 1924–1925 Weymouth 1925–1929 Brentford 62 (2)1929–1932 Gillingham 109 (0)1932–19?? Worcester City Evesham Town *Club domes...

Nota: Para por outros significados de Danúbio, veja Danúbio (desambiguação). Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW • CAPES • Google (N • L • A)). (Junho de 2020) Danúbio Rio DanúbioCurso do Danúbio Comprimento 2 845 a 2 888 km Nascente Floresta Negra (Alemanha) Caudal médio 6700 m³/s Foz delta do Danúbio, Mar Negro. (Romênia) �...




