Infinitesimal
| ||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis. Ini adalah nama Batak Toba, marganya adalah Sianturi. Bonar Sianturi Bupati SintangMasa jabatan27 Maret 1989 – 5 April 1994GubernurParjoko SuryokusumoAspar Aswin PendahuluDaniel TodingPenggantiAbdillah Kamarullah Informasi pribadiLahir(1944-06-18)18 Juni 1944Sidikalang, Bataklanden, Tapanuli, Hindia BelandaMeninggal22 Mei 2022(2022-05-22) ...

Untuk kegunaan lain, lihat Elizabeth. ElisabetElisabet (kiri) dikunjungi Maria, oleh Philippe de ChampaigneBerbudi BaikLahirAbad 1 SMHebron (Joshua 21:11:niv)MeninggalAbad 1 SM (atau mendekati Masehi)(mungkin Hebron)Dihormati diGereja Katolik RomaGereja Ortodoks TimurGereja Ortodoks OrientalGereja AnglikanGereja LutheranIslamPesta5 November(Gereja Katolik Roma, Lutheran)5 September (Gereja Ortodoks Timur, Anglikan) Elisabet (Ibrani: אֱלִישֶׁבַע / אֱלִישָׁבַע Ĕlîš...

Shmuel HaNaviLingkunganNegara IsraelProvinsiYerusalemKotaYerusalemZona waktuUTC+3 (EAT) • Musim panas (DST)UTC+3 (EAT) Shmuel HaNavi adalah sebuah lingkungan di kota suci Yerusalem di Provinsi Yerusalem, tepatnya di sebelah timur Israel.[1] Referensi ^ National Geospatial-Intelligence Agency. GeoNames database entry. (search Diarsipkan 2017-03-18 di Wayback Machine.) Accessed 12 May 2011. lbsLingkungan di YerusalemLingkungan-lingkungan Yerusalem sebelah timur garis ge...

For other uses, see Sail Rock (disambiguation). Parus Rock Sail Rock, or Parus Rock (Russian: скала́ Па́рус, skala Parus), is a natural sandstone monolith of late Cretaceous age[1] located on the shore of the Black Sea, in Krasnodar Krai, Russia. It resembles the outline of a ship's sail, hence its name. The monolith lies 17 km to the southeast of Gelendzhik, near the village of Praskoveyevka (which is about 500 m from the coast) and the farmstead of Dzhankhot (a...

Founder of Quanta Technology This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (September 2021) (Learn how and when to remove this template message) Damir NovoselBorn(1957-12-21)21 December 1957SR Bosnia and Herzegovina, YugoslaviaEducationUniversity of Tuzla University ...

Rearrangement of sectors on a hard disk into contiguous units Defrag redirects here. For other uses, see Defrag (disambiguation). Disk Defragmenter redirects here. For the Microsoft Windows utility, see Microsoft Drive Optimizer. Visualization of fragmentation and then of defragmentation In the maintenance of file systems, defragmentation is a process that reduces the degree of fragmentation. It does this by physically organizing the contents of the mass storage device used to store files int...

Outline of HBO's international television channels This article is about pay television channels outside the United States. For the American pay television network, see HBO. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of HBO international channels – news · newspapers · books · scholar · JSTOR (Febru...
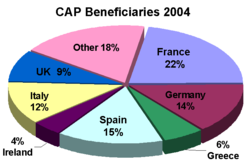
Financial calculation reducing the UK's EU contributions The UK rebate (or UK correction) was a financial mechanism that reduced the United Kingdom's contribution to the EU budget in effect since 1985. It was a complex calculation which equated to a reduction of approximately 66% of the UK's net contribution – the amount paid by the UK into the EU budget less receipts from the EU budget.[1][2] Based on a net contribution of €11.7 (£9.6) billion in 2016, the UK Treasu...

1991 song by Kylie Minogue I Guess I Like It Like That12 promotional vinyl coverPromotional single by Kylie Minoguefrom the album Let's Get to It A-sideIf You Were with Me NowReleasedOctober 1991Genre Techno-pop[1] dance[2] house Length6:00 (album version) 3:30 (edit)LabelMushroomSongwriter(s) Mike Stock Pete Waterman Kylie Minogue Phil Wilde Jean-Paul de Coster Producer(s) Mike Stock Pete Waterman Audio videoI Guess I Like It Like That on YouTube I Guess I Like It Like That i...

Ramagundam Police CommissionerateCommon nameRamagundam City PoliceAbbreviationరామగుండం పోలీస్ కమీషనరేట్ , रामगुऺडम पुलीस कमिषनरे्टMottoService Pride DedicationAgency overviewFormed11 October, 2016EmployeesCommissioner of Police Deputy commissioner Additional Deputy CommissionersPolice Inspectors Assistant Police Inspectors Sub InspectorsJurisdictional structureOperations jurisdictionPeddapalli and ...

Abbas TyrewalaLahir15 Mei 1974 (umur 49)Mumbai, Maharashtra, IndiaTempat tinggalMumbai, Maharashtra, IndiaPekerjaanSutradara, penulis cerita, penulis naskah, penulis dialogTahun aktif2001-sekarangSuami/istriPakhi Tyrewala Abbas Tyrewala adalah seorang penulis cerita, penulis naskah, penulis dialog dan sutradara asal India.[1] Setelah menjalani karier sebagai penulis naskah dan dialog pada awal 2000an, dengan film-film pemenang penghargaan seperti Maqbool (2003) dan Munnabha...

Rondacomune Ronda – Veduta LocalizzazioneStato Spagna Comunità autonoma Andalusia Provincia Malaga TerritorioCoordinate36°44′14″N 5°09′53″W / 36.737222°N 5.164722°W36.737222; -5.164722 (Ronda)Coordinate: 36°44′14″N 5°09′53″W / 36.737222°N 5.164722°W36.737222; -5.164722 (Ronda) Altitudine723 m s.l.m. Superficie481,31 km² Abitanti36 827 (2009) Densità76,51 ab./km² Comuni confinantiAlcalá del Val...

South African radio station 947JohannesburgBroadcast areaGauteng (Terrestrial FM)Africa (DStv Channel 879)Frequency94.7 MHzProgrammingFormatContemporaryOwnershipOwnerPrimedia (private)Sister stations94.5 Kfm Radio 702 CapeTalkHistoryFirst air date1 September 1964LinksWebcastLive streamWebsitehttps://947.co.za 947 (formerly 94.7 Highveld Stereo) is a radio station that broadcasts on the 94.7FM frequency from Johannesburg, Gauteng, South Africa. History The station first went on the air on 1 Se...

لمعانٍ أخرى، طالع كرمة (توضيح). اضغط هنا للاطلاع على كيفية قراءة التصنيف الكرمة الكرمة الكاليفورنية كرمة (نبات) المرتبة التصنيفية جنس[1] التصنيف العلمي النطاق: حقيقيات النوى المملكة: النباتات الشعبة: البذريات الشعيبة: مستورات البذور الرتبة: الكرميات الفصيلة: ا...

Božena Viková-KunětickáFonctionsMember of the Bohemian Diet (d)Membre du Sénat tchécoslovaqueMembre de l'Assemblée nationale révolutionnaire de Tchécoslovaquie (d)BiographieNaissance 30 juillet 1862PardubiceDécès 18 mars 1934 (à 71 ans)LibočanyNationalités tchécoslovaqueautrichienneActivités Écrivaine, femme politique, poétesse, dramaturge, actriceAutres informationsParti politique Parti des jeunes Tchèquesmodifier - modifier le code - modifier Wikidata Božena Vikova-...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (ديسمبر 2020) جميرا أبراج الإماراتمعلومات عامةنوع المبنى ناطحة سحاب المنطقة الإدارية إ...

Election in Massachusetts Main article: 1844 United States presidential election 1844 United States presidential election in Massachusetts ← 1840 November 1 - December 4, 1844 1848 → Turnout65.8%[1] 0.9 pp Nominee Henry Clay James K. Polk James G. Birney Party Whig Democratic Liberty Home state Kentucky Tennessee Michigan Running mate Theodore Frelinghuysen George M. Dallas Thomas Morris Electoral vote 12 0 0 Popular vote 67,062 53,039 ...

Akbar Hashemi Rafsanjani اکبر هاشمی رفسنجانی Presiden Republik Islam Iran ke-4Masa jabatan3 Agustus 1989 – 2 Agustus 1997Wakil PresidenHassan HabibiPemimpinAli KhameneiPendahuluAli KhameneiPenggantiMohammad Khatami Informasi pribadiLahir(1934-02-15)15 Februari 1934Nough, IranMeninggal8 Januari 2017(2017-01-08) (umur 82)Tajrish, IranPartai politikAsosiasi Ulama MilitanSunting kotak info • L • B Akbar Rafsanjani di sampul majalah TIME edisi Timur T...

Questa voce o sezione sull'argomento trasporto pubblico non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Heathrow ExpressServizio di trasporto pubblicoStati Regno Unito CittàLondra InizioLondra Heathrow FineLondra Paddington Apertura1998 GestoreHeathrow Express Operating Authority N. staz...

Upcoming Namma Metro station under Blue Line Agara Namma Metro stationUnder Construction of this metro station as of April 2024 under Phase 2A of Blue Line of Namma MetroGeneral informationLocationAH45, Agara Village, 1st Sector, HSR Layout, Bengaluru, Karnataka 560034Coordinates12°55′14″N 77°38′37″E / 12.92053°N 77.64359°E / 12.92053; 77.64359Owned byBangalore Metro Rail Corporation Ltd (BMRCL)Operated byNamma MetroLine(s)Blue LinePlatformsSide platform (T...









