Knuths pilnotation
| |||||||||||||||||||||
Read other articles:

La Rete IGM95 è una rete geodetica fondamentale italiana nata nel 1992, che si affianca alla rete trigonometrica classica. Indice 1 Descrizione 2 Informazioni nella monografia 3 Voci correlate 4 Collegamenti esterni Descrizione Esempio di vertice geodetico su cima montuosa La rete è costituita da punti geodetici o capisaldi, simili alle vecchie pietre miliari romane, costituiti da un basamento orizzontale in cemento e un cippo cilindrico leggermente appuntito in alto. Ogni caposaldo viene i...

Non-elected workforce of the US government This article is part of a series on thePolitics of the United States Federal government Constitution of the United States Law Taxation Policy Legislature United States Congress House of Representatives Speaker Mike Johnson (R) Majority Leader Steve Scalise (R) Minority Leader Hakeem Jeffries (D) Congressional districts (List of congressional districts) Senate President Kamala Harris (D) President Pro Tempore Patty Murray (D) Majority Leader Chuck Sch...

Skema kapal selam kelas Shchuka seri V bis 2. Sejarah Soviet Union Diluncurkan 6 November 1934Dicoret 11 September 1954Status Dibesituakan dan dibongkarLencana Ciri-ciri umum Kelas dan jenis Kapal selam kelas-ShchukaBerat benaman 593 ton (permukaan) 705,7 ton (menyelam)Panjang 58,8 mLebar 6,2 mSarat air 3,9 mKecepatan 13,5 knot (permukaan) 8,5 knot (menyelam)Daya tahan 20 hari di permukaanKedalaman uji coba 90 mAwak kapal 37 kruSenjata 2 buah senapan anti-pesawat 45mm 21-K (1000 peluru) Tabu...
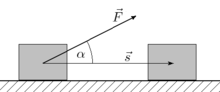
У этого термина существуют и другие значения, см. Работа. Работа A , W {\displaystyle A,W} Размерность L2MT−2 Единицы измерения СИ Дж СГС эрг Примечания скалярная величина Механическая работаКлючевые статьи Работа в физике Механическая работа Закон сохранения энергии Термодинамиче...

Pemburu-peramu suku Mbendjele sedang membagi-bagikan daging. Artikel ini merupakan bagian dariseri mengenai:Komunisme KonsepFilosofi Marxis Ekonomi Marxian Materialisme historis Nilai lebih Mode produksi Perjuangan kelas Masyarakat Tanpa Kelas Internasionalisme proletariat Revolusi Dunia Aspek Negara komunis Partai komunis Revolusi komunis Simbolisme komunis Komunisme dan agama Sejarah komunisme Jenis Marxisme Leninisme Trotskyisme Maoisme Luxemburgisme Titoisme Stalinisme Castroisme Guevaris...

Berikut ini adalah nama-nama tempat yang disebutkan dalam Perjanjian Baru di Alkitab Kristen Berhubungan dengan Yesus Kristus Galilea Ainon (Ænon) - sebuah tempat dekat Salim di tepi sungai Yordan di mana Yohanes Pembaptis membaptiskan orang-orang yang datang kepadanya sebab di situ banyak air (Yohanes 3:23).[1][2] Betsaida - antara lain tempat penyembuhan seorang buta (Markus 8)[3][4] Genesaret: Kota yang sekarang sudah tidak ada lagi ini terletak di pantai b...

Mannō まんのう町Kota kecil BenderaLambangLokasi Mannō di Prefektur KagawaNegara JepangWilayahShikokuPrefektur KagawaDistrikNakatadoLuas • Total194 km2 (75 sq mi)Populasi (Oktober 1, 2015) • Total18.377 • Kepadatan94,7/km2 (2,450/sq mi)Zona waktuUTC+9 (Waktu Standar Jepang)Kode pos766-0022Nomor telepon0877-73-0100Alamat430 Yoshinoshimo,Mannō-chō, Nakatado-gun, Kagawa-kenSitus webSitus web resmi Mannō (まん�...

Wilhelm Liebknecht Wilhelm Martin Philipp Christian Ludwig Liebknecht[1] (29 Maret 1826 – 7 Agustus 1900) adalah seorang sosial demokrat Jerman dan salah satu pendiri utama Partai Sosial Demokrat Jerman. Karier politiknya merupakan sebuah proyek mempelopori pencampuran teori revolusioner Marxis dengan praktik akvitivitas politik hukum. Di bawah kepemimpinannya, partainya bertumbuh dari kelompok kecil menjadi partai politik terbesar di Jerman. Ia merupakan ayah dari Kar...

1944 film directed by Edward Dmytryk For the remake starring Robert Mitchum, see Farewell, My Lovely (1975 film). Murder, My Sweet(Farewell, My Lovely)theatrical release posterDirected byEdward DmytrykScreenplay byJohn PaxtonBased onFarewell, My Lovely1940 novelby Raymond ChandlerProduced byAdrian ScottStarringDick PowellClaire TrevorAnne ShirleyNarrated byDick PowellCinematographyHarry J. WildEdited byJoseph NoriegaMusic byRoy WebbDistributed byRKO Radio PicturesRelease date December 9,...
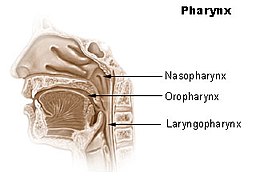
Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. FaringeTesta e ColloFaringe Anatomia del Gray(EN) Pagina 1141 Arteriaarteria faringea ascendente Venapharyngeal plexus IdentificatoriMeSHA03.556.750, A04.623 e A14.724 TAA05.3.01.001 FMA46688 Modifica dati su Wikidata · Manuale La faringe (gr. φάρυγξ pharynix) è il canale muscolo-membranoso del ca...

Sweet, potato-based treat Potato doughnutA sampler of potato doughnuts from Spudnuts Coffee Shop in Charlottesville, Virginia, United StatesAlternative namesSpudnutTypeDoughnutPlace of originUnited StatesMain ingredientsPotato Media: Potato doughnut Potato doughnuts, sometimes called a Spudnut, are a type of doughnut, typically sweet, made with either mashed potatoes or potato starch instead of flour, the most common ingredient used for doughnut dough. Potato doughnuts tend to be li...

Tao Zhiyue Gubernur XinjiangMasa jabatan1946 – Maret 1946PendahuluWu ZhongxinPenggantiZhang Zhizhong Informasi pribadiLahir1892Kota praja Xianfeng, Ningxiang, Hunan, Dinasti QingMeninggal26 Desember 1988(1988-12-26) (umur 95–96)KebangsaanTiongkokPartai politikPartai Komunis Tiongkok (sejak 1982)KuomintangPenghargaan sipil Medali Pembebasan (Kelas Pertama) (1955)Karier militerPihakRepublik Tiongkok-1928Republik Rakyat TiongkokDinas/cabang Kelompok Hunan (1914–26) Tentara Re...

Численность населения республики по данным Росстата составляет 4 003 016[1] чел. (2024). Татарстан занимает 8-е место по численности населения среди субъектов Российской Федерации[2]. Плотность населения — 59,00 чел./км² (2024). Городское население — 76,72[3] % (20...

Para otros usos de este término, véase Fénix (desambiguación). Miniatura del Bestiario de Aberdeen: ave fénix renaciendo de sus cenizas. El fénix que supera la Maison de la Louve en Bruselas. En la mitología griega, el fénix (en griego antiguo, φοῖνιξ[1][2]; romanización, phoînix) es un ave de larga vida que se regenera de las cenizas de su predecesor. Según algunas fuentes, el fénix muere en un espectáculo de llamas y combustión, aunque hay otras ...

United States Navy lead ship Gato-class submarine For other ships with the same name, see USS Gato. USS Gato (SS-212) off Mare Island Navy Yard on 29 November 1944 History United States BuilderElectric Boat Company, Groton, Connecticut[1] Laid down5 October 1940[1] Launched21 August 1941[1] Commissioned31 December 1941[1] Decommissioned16 March 1946[1] Stricken1 March 1960[1] Honors andawards 13 × battle stars Presidential Unit Citati...

موتور بمب أزادغان موتورپم پازادگان - قرية - تقسيم إداري البلد إيران المحافظة كرمان المقاطعة أرزوئیة الناحية الناحية المركزية (مقاطعة أرزوئية) القسم الريفي Arzuiyeh السكان التعداد السكاني 20 نسمة (إحصاء 2006) معلومات أخرى التوقيت توقيت إيران (+3:30 غرينيتش) توقيت صيفي...

Research park in North Carolina, United States 35°54′29″N 78°51′46″W / 35.90806°N 78.86278°W / 35.90806; -78.86278 Research Triangle ParkRTP headquarters at 12 Davis DriveMottoInspiring bold ideasEstablished1959 (1959)LocationResearch Triangle, North CarolinaWebsiteRTP.org Research Triangle Park (RTP) is the largest research park in the United States,[1][2][3] occupying 7,000 acres (2,833 ha) in North Carolina and hosting m...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Tratto gastrointestinale I lassativi (purganti, evacuanti, anticostipativi) sono sostanze o composti che stimolano la motilità intestinale (peristalsi) in contrasto agli antidiarroici che la inibiscono. Sono quindi farmaci che curano la stitichezza, la quale riduce o impedisce una corretta defecazione. Le pur...

Self-portrait at the age of 25[1] Dominique Lang (1874–1919) is considered to be Luxembourg's most important Impressionist painter. He painted both portraits and landscapes although he was employed as a high-school teacher.[2] Career After completing his studies in 1901, he embarked on a Pre-Raphaelite phase when he painted the Baptism of Christ, a fresco in the church at Junglinster followed by paintings for the stations of the cross in the new church at Dudelange. Travelli...

Uruguayan footballer (born 1976) In this Spanish name, the first or paternal surname is Recoba and the second or maternal family name is Rivero. Álvaro Recoba Recoba with Nacional in 2012Personal informationFull name Álvaro Alexánder Recoba RiveroDate of birth (1976-03-17) 17 March 1976 (age 48)Place of birth Montevideo, UruguayHeight 1.77 m (5 ft 10 in)Position(s) Attacking midfielder, forwardYouth career DanubioSenior career*Years Team Apps (Gls)1994–1995 Da...


















