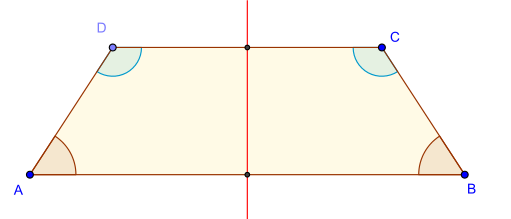
Trapèze
| |||||||||||||||||||||
Read other articles:

Nintendo Co., Ltd.Lambang Nintendo, digunakan sejak 2016.Kantor Pusat Nintendo di Kyoto.Nama asli任天堂株式会社Nama latinNintendō kabushikigaishaSebelumnyaYamauchi Nintendo & Co. (1933–1951)Nintendo Playing Card Co. Ltd. (1951–1963)JenisPublikKode emitenNasdaq: NTDOYNasdaq: NTDOFTYO: 7974ISINJP3756600007IndustriIndustri permainan videoElektronik konsumenDidirikan23 September 1889; 134 tahun lalu (1889-09-23)PendiriFusajiro YamauchiKantorpusatKyoto, JepangWilayah...

Hasapi dengan satu senar. Hasapi adalah salah satu alat musik tradisional Batak Toba yang dikelompokkan ke dalam alat musik dawai atau senar, dalam bahasa Indonesia sering disebut Kecapi Batak.[1] Jenis-jenis Hasapi Hasapi terdiri dari: Hasapi ende (pluked lute dua senar) adalah instrumen pembawa melodi dan merupakan instrumen yang dianggap paling utama dalam ensambel gondang hasapi. Hasapi doal (pluked flude dua senar), instrumen ini sama dengan hasapi ende namun dalam permainannya h...

Duta Besar Indonesia untuk Britania RayaMerangkap Irlandia dan IMOLambang Kementerian Luar Negeri Republik IndonesiaPetahanaDesra Percayasejak 26 Oktober 2020Kementerian Luar NegeriKedutaan Besar Republik Indonesia di LondonKantorLondon, Britania RayaDitunjuk olehPresiden IndonesiaPejabat perdanaSubandrioDibentuk1949Situs webkemlu.go.id/london/id Berikut adalah daftar diplomat Indonesia yang pernah menjabat Duta Besar Republik Indonesia untuk Kerajaan Britania Raya: No. Foto Nama Mulai m...

Paleolitik akhir, Venus dari Willendorf, diperkirakan diukir pada 24.000–22.000 SM Dewi Ibu adalah dewi atau sosok perempuan yang melambangkan atau merupakan perwujudan kekuatan alam, sifat keibuan, kesuburan, penciptaan, kehancuran, atau melambangkan kemurahan atau kelimpahan anugerah bumi. Ketika disamakan dengan bumi atau kekuatan alam, maka dewi ini biasanya disebut sebagai Ibu Bumi atau Ibu Pertiwi. Banyak dewi-dewi dalam berbagai bentuk kepercayaan melambangkan sifat keibuan dalam sat...

American television news correspondent (born 1943) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: David Martin journalist – news · newspapers · books · scholar · JSTOR (February 2024) (Lea...

IUCN conservation category Threatened redirects here. For the Michael Jackson song, see Invincible (Michael Jackson album). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Threatened species – news · newspapers · books · scholar · JSTOR (December 2008) (Learn how and when to remove this template message) Con...

Video game blog This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: VG247 – news · newspapers · books · scholar · JSTOR (November 2023) (Learn how and when to remove this template message) The topic of thi...

Bus rapid transit route in Vancouver, Washington, U.S. The Vine on Mill PlainA westbound Red Line bus at 157th Avenue StationOverviewSystemThe VineOperatorC-TranStatusOpenBegan serviceOctober 1, 2023 (October 1, 2023)RouteLocaleVancouver, Washington, U.S.StartTurtle Place, Downtown VancouverViaMill Plain BoulevardEndMill Plain Transit CenterLength10 mi (16 km)Stations37ServiceLevelDaily Route diagram Legend Mill Plain Transit Center Tech Center Drive 164th Avenue 157th Av...

Fernando Veneranda Fernando Veneranda con la tuta di allenamento del Palermo Nazionalità Italia Calcio Ruolo Allenatore (ex attaccante) Termine carriera 1973 - giocatore1992 - allenatore CarrieraGiovanili 19??-1959 Sangiorgese1960-1962 FiorentinaSquadre di club1 1959-1960 Sangiorgese27 (?)1960-1962 Fiorentina0 (0)1962-1964 Prato63 (14)1964-1966 Brescia29 (3)1966-1967 Potenza33 (6)1967-1968 Palermo15 (2)1968-1969 Genoa7 (1)1969-1973 Mat...

North Hollywood redirects here. For the film, see North Hollywood (film). Neighborhood in Los Angeles, California, United States of AmericaNorth HollywoodNeighborhood Top: St. Charles Borromeo Church (left), North Hollywood High School (right); bottom: El Portal Theatre (left), Academy of Television Arts & Sciences (right).Nickname: NoHoNorth HollywoodLocation within Los Angeles/San Fernando ValleyShow map of San Fernando ValleyNorth HollywoodNorth Hollywood (the Los Angeles metropol...

He Got GameRay Allen e Denzel Washington in una scena del filmTitolo originaleHe Got Game Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1998 Durata137 min Rapporto1,85:1 Generedrammatico, sportivo RegiaSpike Lee SoggettoSpike Lee SceneggiaturaSpike Lee ProduttoreSpike Lee, John Kilik Casa di produzione40 Acres & a Mule Filmworks, Touchstone Pictures FotografiaMalik Hassan Sayeed MontaggioBarry Alexander Brown Effetti specialiRandall Balsmeyer MusicheAaron Coplan...

Will & GraceLogo della serieTitolo originaleWill & Grace PaeseStati Uniti d'America Anno1998-2020 Formatoserie TV Generesitcom Stagioni11 Episodi246 Durata22 min (episodio) Lingua originaleinglese Rapporto4:3 (st. 1-6)16:9 (st. 7-11) CreditiIdeatoreDavid Kohan, Max Mutchnick RegiaJames Burrows Interpreti e personaggi Eric McCormack: Will Truman Debra Messing: Grace Adler Sean Hayes: Jack McFarland Megan Mullally: Karen Walker Doppiatori e personaggi Francesco Prando: Will Truman Franc...

Disambiguazione – Se stai cercando la frazione di Livraga in provincia di Lodi, vedi Pantigliate (Livraga). Questa voce sull'argomento centri abitati della città metropolitana di Milano è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Pantigliatecomune Pantigliate – VedutaSantuario della Madonna della Provvidenza LocalizzazioneStato Italia Regione Lombardia Città metropolitana Milano AmministrazioneSindacoAbate Franco (lista civi...

Richard CarleLahirCharles Nicholas Carleton(1871-07-07)7 Juli 1871Somerville, Massachusetts, Amerika SerikatMeninggal28 Juni 1941(1941-06-28) (umur 69)North Hollywood, California, Amerika SerikatPekerjaanPemeranTahun aktif1915–1941 Carle digambar dalam sebuah iklan surat kabar, 1909 Richard Carle (nama lahir Charles Nicholas Carleton, 7 Juli 1871 – 28 Juni 1941) adalah seorang pemeran panggung dan film serta pembuat sandiwara dan pengarah panggung asal Amerika Ser...

1959 Christmas carol Cover of original 1959 edition of sheet music of Little Donkey Little Donkey is a popular Christmas carol, written by British songwriter Eric Boswell in 1959, which describes the journey by Mary the mother of Jesus to Bethlehem on the donkey of the title.[1] The first version to chart was by Gracie Fields, followed a fortnight later by The Beverley Sisters, who overtook her in the charts by Christmas. The song became No. 1 in the UK Sheet Music Chart[2] fr...

British Army officer and politician (1909-1991) William Sidney redirects here. For other uses, see William Sidney (disambiguation). The Right HonourableThe Viscount De L'IsleVC, KG, GCMG, GCVO, KStJ, PCSidney in 196215th Governor-General of AustraliaIn office3 August 1961 – 7 May 1965MonarchElizabeth IIPrime MinisterRobert MenziesPreceded byLord DunrossilSucceeded byLord CaseySecretary of State for AirIn office31 October 1951 – ...

Royal Navy admiral (1806–1875) Sir Henry KellettSir Henry KellettBorn(1806-11-02)2 November 1806Tipperary County, IrelandDied1 March 1875(1875-03-01) (aged 68)Tipperary County, IrelandAllegianceUnited KingdomService/branchRoyal NavyYears of service1822–1871RankVice admiralCommands heldChina StationJamaica DivisionHMS ResoluteHMS HeraldHMS StarlingBattles/warsFirst Opium WarAwardsKnight Commander of the Order of the Bath Vice Admiral Sir Henry Kellett, KCB (2 Novem...

Connections between businesses operated by the Overseas Chinese community in Southeast Asia This article is about the Overseas Chinese business network. For the Cold War term, see Bamboo Curtain. For the term about the employment advancement barriers that East Asians face in the Western world, see Bamboo ceiling. Bamboo networkCountries and territories Cambodia Indonesia Laos Malaysia Myanmar Philippines Singapore Thailand VietnamLanguages and language ...

American television award ceremony Emmy and Emmie redirect here. For other uses, see Emmy (disambiguation). This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Emmy Awards – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) Emmy AwardsComedian Garry Shandling during the rehearsal of the 45th Primetime Emm...

Spanish philosopher, theologian, Catholic apologist, sociologist and political writer Balmes redirects here. For other uses, see Balmes (disambiguation). Jaime BalmesBornJaime Luciano Antonio Balmes y Urpiá28 August 1810Vic, Catalonia, SpainDied9 July 1848 (1848-07-10) (aged 37)Vic, Catalonia, SpainBurial placeCathedral of St Peter of VicNationalitySpanishAlma materUniversity of CerveraOccupation(s)Theologian, presbyter and writerEra19th-century philosophyRegionWestern philoso...