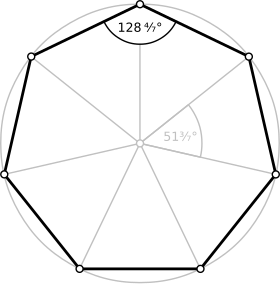
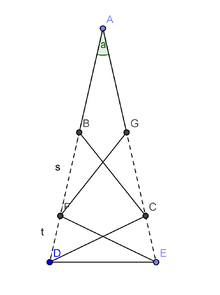
Heptagone
| |||||||||||||||||||||||
Read other articles:

Halaman ini berisi artikel tentang album. Untuk teori, lihat multimesta. MultiversesAlbum studio karya FeastDirilis18 September 2017 (2017-09-18)Studio Soundpole Studio Sams Studio Genre Rock Durasi54:15Label .Feast Karma Leeds Produser Wisnu Ikhsantama W. Bam Mastro Baskara Putra Hazen Mardial Janitra Satriani Johanes Bosco Kronologi Feast Multiverses(2017) Beberapa Orang Memaafkan(2018) Singel dalam album Multiverses Wives of ÐÇСÐˋ / Gojira (We Belong Dead)Dirilis: 24 Mei 2017&...

The Center for Public IntegrityTanggal pendirianMaret 1989; 35 tahun lalu (1989-03)PendiriCharles LewisNPWP 54-1512177Tipe501(c)(3)FokusJurnalisme investigasiLokasiWashington DCMetodeYayasan didanai anggotaTokoh pentingPeter Bale (CEO)Situs webwww.publicintegrity.org Center for Public Integrity (CPI, arti harfiah: Pusat untuk Integritas Masyarakat) adalah organisasi jurnalisme investigasi nirlaba Amerika Serikat dengan misi mengungkap penyalahgunaan kekuasaan, korupsi, dan pengabaian tug...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Hennessey Venom F5InformasiProdusenHennessey Special VehiclesMasa produksi2020ãsekarangModel untuk tahun2021ãsekarangPerakitanSealy, Texas, Amerika Serikat (Hennessey Performance Engineering)Bodi & rangkaKelasMobil sport (S)Bentuk ker...

Hermanta Direktur Perkapalan Dan Kepelautan Informasi pribadiLahir15 Januari 1973 (umur 51)Jakarta IndonesiaAlma materSepa (1996)Karier militerPihak IndonesiaDinas/cabang Kementerian Perhubungan Republik IndonesiaMasa dinas1996ãsekarangPangkat Brigadir Jenderal PolisiSatuanPolairSunting kotak info ã L ã B Brigjen. Pol. Hermanta, SH., MM. (lahir 15 Januari 1973) adalah seorang perwira tinggi Polri yang mengemban amanat sebagai Direktur Perkapalan Dan Kepelautan D...

ÅůŧŧŃŧÅç îîîšŧî ÅÏÅ¡îÅ£ÅçŧŧŃîîî 16 182 îÅçÅ£. ŠůîîÅçÅ£ÅçŧšÅç ÅÀÅçîÅÝÅ¡î: 14 246 îÅçÅ£. (2011) ÅËŃîÅýůîÅ¡î: 1 936 ã îÅçÅ£. (2011) Å₤ÅñîŤ îÅÑŧŃîîîšŧſ îÅñîŤ Å ÅçţšŰšî Å°îÅçŤŃŤůîŃţšîÅ¡ÅñÅ¥, Å¢îůÅýŃîţůÅýÅ¡Åç Åî ŃÅÇÅ¡î Åý îîîšŧî ŠŃÅÇîîÅýÅçŧŧîÅç ŧůîŃÅÇî îîîšŧî, îŤîůšŧîî ÅîŃšîî ŃÅÑÅÇÅçŧšÅç îîîšŧî, îţŃÅýůŤš ÅÅçÅÇšůîůſţî ŧů ÅšŤšÿ¢§...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KPWW ã news ôñ newspapers ôñ books ôñ scholar ôñ JSTOR (April 2015) (Learn how and when to remove this template message) Radio station in Hooks, TexasKPWWHooks, TexasBroadcast areaTexarkana, TexasãArkansasFrequency95.9 MHzBrandingPower 95-9ProgrammingLanguage(s)EnglishFormatTop 40...

ÄÏìÄ¿ìÄÏìÄÏĈ ÄÏìÄ°ììÄ°ÄÝìÄˋ ÄÏìÄ°ìÄÝÄÏìììììÄˋ Ä°ììÄ°ÄÝÄÏ Ä°ìÄÝÄÏìììì Ä°ììÄ°ÄÝÄÏ Ä°ìÄÝÄÏìììì ĈĿÄ₤ìì ì ÄçÄ₤ÄÝì - ĈĿÄ₤ìì ÄÏìÄ¿ìÄÏìÄÏĈ ÄÏìÄ°ììÄ°ÄÝìÄˋ ÄÏìÄ°ìÄÝÄÏìììììÄˋ ìì ÄÏìÄ¿ìÄÏìÄÏĈ ÄÏìĨìÄÏÄÎìÄˋ ÄÏìĈì ĈĘì Ä¿ Ä´ìì Ä°ììÄ°ÄÝÄÏ ìÄ°ìÄÝÄÏìììì.[1][2][3][4][5] ì ìÄÏÄÝìÄˋ Ä´ìì ÄÏìÄ´ìÄ₤ìì ìįì ì ìÄÏÄÝìÄˋ Ä¿ÄÏì Äˋ ìì ÄÝĘĿìÄˋ ììÄ₤ììĈìì:...

Synagogue in Lebanon Deir el Qamar SynagogueìììÄ° Ä₤ìÄÝ ÄÏììì ÄÝReligionAffiliationOrthodox JudaismRiteSephardicEcclesiastical or organizational statusopenLocationLocationChouf, LebanonArchitectureCompleted1638 The Deir el Qamar Synagogue, in Deir el Qamar, a village in south-central Lebanon, is the oldest synagogue in Mount Lebanon.[1] The synagogue was built in the 17th century, during the Ottoman era in Lebanon, to serve the local Jewish population, some of whom were part of ...

American artistic gymnast McKayla MaroneyMaroney in 2012Personal informationBorn (1995-12-09) December 9, 1995 (age 28)Aliso Viejo, California, U.S.ResidenceNewport Beach, California, U.S.Height5 ft 4 in (163 cm)[1]DisciplineWomen's artistic gymnasticsLevelSenior International EliteYears on national team2010ã14 (USA)GymAll Olympia Gymnastics Center (AOGC)Head coach(es)Artur Akopyan[2]Assistant coach(es)Galina MarinovaFormer coach(es)Jenny Z...

Phyllis AllenAllen bersama Mack Swain (berdiri), Mabel Normand dan Charlie Chaplin di Getting Acquainted (1914)Lahir(1861-11-25)25 November 1861Pulau Staten, New York, U A.S.Meninggal26 Maret 1938(1938-03-26) (umur 76)Los Angeles, California, A.S.PekerjaanAktris, komedian, vaudevillianTahun aktif1913ã1923 Phyllis Allen (25 November 1861 – 26 Maret 1938) adalah seorang komedian dan aktris film bisu asal Amerika Serikat. Dia bekerja dengan Charles Chaplin, Mabel Nor...

Jerzy Franciszek Kulczycki (tedesco: Georg Franz Kolschitzky, ucraino: ÅÛîîÅ¿-ÅÊîůŧî ÅîÅ£îîÅ¡îſ, Jurij Franc Kul'áyc'kyj; ca 1640 ã Vienna, 19 febbraio 1694) û´ stato un diplomatico, nobile e imprenditore ucraino naturalizzato polacco.[1] Indice 1 Ipotesi di origine 2 Biografia 3 Note 4 Altri progetti Ipotesi di origine Come scrive il ricercatore polacco Zygmunt Abragamowych (Dizionario biografico polacco, 1970), ci sono pochi documenti e fonti su Yuriy Kulchytsk...

University in Camerino, Italy This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Camerino ã news ôñ newspapers ôñ books ôñ scholar ôñ JSTOR (June 2023) (Learn how and when to remove this message) University of CamerinoUniversitû degli Studi di CamerinoLatin: Camerinum UniversitasTypeState-supportedEs...

ÌÙÊÌÂÓÛÍ₤Ò§Í Í¨ð¡ÕÓ´ÌÒ¨ÌýÒÏÈÓÍ¥Ó´ÒçÌÿ¥Õ´ÍÍ ÍÛ¿ÓÍÓÀÛÌÏÌ Ì°Ò¨Ò₤Í₤ÎÐ (2023Í¿Ç1Ì5ÌË)Ò₤ñÍÍˋÌ ÀÌ ¡Í Ñð¡ÙÓÕÒ₤₤ð£ËÌ¿ÍÒ¢Ó₤ÌÀÓÛÐÒ₤ÎÌ Ò₤ñÍÒÏÌÀÓÛÓÒÛ´ÒÛ¤ÕÀçÐ ÍÍ§Ó¡Í ° ð¡£ÕÀÍÒÀ´ ÓÇÂÍ¥ Í§Í Óð¤Ị̈ͥ Ó°Ìý¿Í´Õ ͧÕýÕÂÓÛ ÌÙÎÒÈ Õ´Õÿ¥Íð¤ÿ¥ ÍÛÌ¿Ò₤ÙÒ´ ð¤¤ÍÈÓçÝÒ´ ð¤¤ÍÈÍ₤ͤΠÓÒýÓ Í¤ÓÓ ÌÙ£ð¤ÀÓ ÒˆÌÓ Ò¯ÌÓ ÍÊÝð¡Ó Í´ÒÓ Ò₤ÍÙÓ Í¤ÍÈÕ ҢÍÈÕÂ Ó Êð¤ÏÕ ÍÓçÕ ÓÓÎÓ ÌÙ£Í Í§Í¤ ...

ÌÙÊÌÀÓÛͤҴӨ ÒÌýÀÌÍ ÍÌ£Ó£Í ´ÌÍ ÍÛ¿ÒÎÓ¿Ð (2019Í¿Ç3Ì21ÌË)Ò₤ñÒÒÌˋÍ Í¤Ò´ÿ¥Ì¡ ̯ÌÎÒ¢¯ÌÀÓÛÌÌÕÕ£ÐÒ₤ñÍ´ÌÀÓÛÓÒÛ´ÒÛ¤ÕÀçÒÛ´ÒÛ¤ÌÙÊÕÛÕÂÐ ÍÒ´Í Ì₤ÍÎÓ¡§ÓçÝÍÒˋÍ Ó¡§ÓçÝÌÓƒð££ØůîîÅ¥-ÅŃťůîî ÅÅçÅ¥ÅçÅ£ØÝÅ£î ÅÂŃØůÅçÅýÍÀÓÍÏÒËÕˋ˜Í¯Ó¿ôñÌÍÀÒÑÍʨ҈2019Í¿Ç3Ì20ÌËÍ´ð££ð££Ì7Í¿ÇÕÎð££ÍˆÍ¯Òð¡¿ôñÓ¤°ÌͯÍñÇÒÑÍʨÒÛƒÓ¨1990Í¿Ç4Ì24ÌËÿ¥ÍÒˋÍ ÒÓÑÙÍÓʃÌð¡£ÓƒˋÍ ÝÍÍÓ¡§ÓçÝÿ¥ ÍÒ´Í Ì₤ÍÎ ÍÒ´Í Ì₤ÍÎ̢ͤ...

Thomas Menino Wali Kota Boston 53Masa jabatan12 Juli 1993 ã 6 Januari 2014PendahuluRaymond FlynnPenggantiMarty WalshPresiden Dewan Kota BostonMasa jabatan1993PendahuluDapper O'NeilPenggantiJames M. KellyKonselor Kota Bostonuntuk Distrik 5Masa jabatan1984ã1993PendahuluDistrik DibentukPenggantiDaniel F. Conley Informasi pribadiLahirThomas Michael Menino(1942-12-27)27 Desember 1942Hyde Park, Boston, MassachusettsMeninggal30 Oktober 2014(2014-10-30) (umur 71)Boston, Massachu...

American businessman, aviator, sailor, and adventurer (1944ã2007) Steve FossettFossett in September 2002BornJames Stephen Fossett(1944-04-22)April 22, 1944Jackson, Tennessee, U.S.DiedSeptember 3, 2007(2007-09-03) (aged 63)Sierra Nevada Mountains, California, U.S.Cause of deathPlane crashAlma materWashington University in St. Louis (MBA)Stanford University (BA)Garden Grove High SchoolKnown forsetting a large number of world records as an adventurer, sailor and aviatorSpou...

Measure of the scattering amplitude of a wave by an isolated atom X-ray atomic form factors of oxygen (blue), chlorine (green), Clã (magenta), and K+ (red); smaller charge distributions have a wider form factor. In physics, the atomic form factor, or atomic scattering factor, is a measure of the scattering amplitude of a wave by an isolated atom. The atomic form factor depends on the type of scattering, which in turn depends on the nature of the incident radiation, typically X-ray, electron...

Title of the king of Eswatini iNgwenyama of EswatiniArms of His Majesty the iNgwenyama of EswatiniIncumbentMswati IIIsince 25 April 1986 DetailsStyleHis MajestyHeir apparentNone declaredFirst monarchMkhulunkosiResidenceLozitha Palace, Lobamba, Eswatini Politics of Eswatini Constitution Human rights LGBT rights Monarchy Ngwenyama (list) Mswati III Ndlovukati (list) Ntfombi Government Prime Minister Russell Dlamini Cabinet Parliament Senate President House of Assembly Speaker Administ...

Culture of the Inuit in the Arctic and Subarctic region This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (June 2021) (Learn how and when to remove this message) This article should specify ...

ð£ÊÍÑͧð¡ÒÎÏ > ÍÌçñÕ (ð£ÊÍÑ) > ÕÏÒñ₤ͧ > ÍÍý¡ÕÀ ÌË̘ > ÍÌçñÕ > ÕÏÒñ₤ÓñÍÌ₤ÒÍÝ > ÍÍý¡ÕÀ ÍÌçñÕÍÍý¡ÕÀÐÛð§Ó§Ûÿ¥1.ÍÍý¡Ó¤ 2.Ìçð¡ÙÓ¤ ÒÕ£ÿ¥ÍƒÐ¨ð£ÕÀШÓñ´Í ËÐÐͤÍÿ¥ ÍÍý¡ÕÀÿ¥ÐÐÈÐÐÐÐÿ¥Ð₤ÐÍÌçñÕÿ¥ÕÏÒñ₤ͧÿ¥ÕÏÒñ₤ÓñÍÌ₤ÒÍÝÐÛÕÀÐ ð¤¤ÍÈ13,566ð¤¤ÐÕÂÓˋ1,162.24km²Ðð¤¤ÍÈÍ₤ͤÎ11.7ð¤¤/km²Ðÿ¥2024Í¿Ç6Ì30ÌËÐð§Ì¯Í¤Ì˜Í¯Í¡°ð¤¤ÍÈÿ¥ ð£Ëð¡ÐÛ2Ó¤ÿ¢§...