ʨßÂáÝÈáåÂæóÂÆöÁêÜ
|
Read other articles:

View of the Tatras from the castle ruin Grodzisko at Skała Polish Jura, Glove Rock (Skała Rękawica) at Ojców National Park Maczuga Herkulesa The Kraków-Częstochowa Upland, also known as the Polish Jurassic Highland or Polish Jura (Polish: Jura Krakowsko-Częstochowska), is part of the Jurassic System of south–central Poland, stretching between the cities of Kraków, Częstochowa and Wieluń. The Polish Jura borders the Lesser Polish Upland to the north and east, the foothills of the W...

Turquie au Concours Eurovision Pays Turquie Radiodiffuseur Radio-télévision de Turquie Participations 1re participation Eurovision 1975 Participations 34 (en 2012) Meilleure place 1er (en 2003) Moins bonne place Dernier (en 1975, 1983 et 1987) Liens externes Page officielle du diffuseur Page sur Eurovision.tv Pour la participation la plus récente, voir :Turquie au Concours Eurovision de la chanson 2012 modifier La Turquie participe au Concours Eurovision de la chanson, de...

Video burung beo yang mengatakan Halo (Hello) setelah dirangkum untuk berbicara oleh orang-orang. Burung beo adalah contoh hewan yang dapat meniru bahasa manusia. Tiggy the talking cat Hewan yang bisa bicara atau adalah hewan selain manusia yang dapat menghasilkan suara atau gerak tubuh yang menyerupai bahasa manusia.[1] Beberapa spesies atau kelompok hewan telah mengembangkan bentuk komunikasi yang secara dangkal menyerupai bahasa verbal, namun, ini biasanya tidak dianggap sebagai ba...
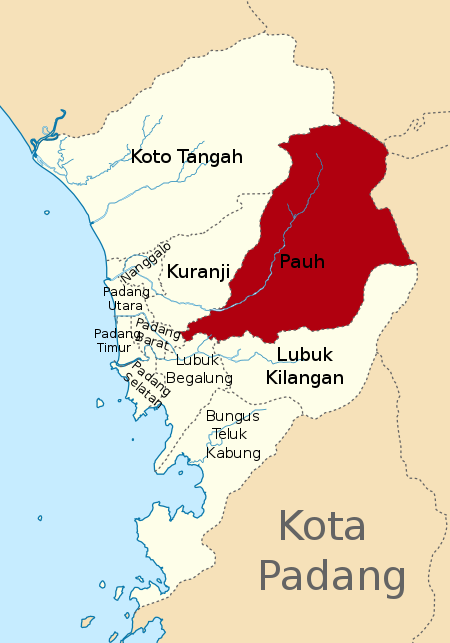
Untuk kecamatan di Kabupaten Sarolangun, lihat Pauh, Sarolangun. PauhKecamatanKantor camat Pauh di Sungai Balang, Cupak Tangah, PauhPeta lokasi Kecamatan PauhNegara IndonesiaProvinsiSumatera BaratKotaPadangPemerintahan • CamatRonny, S.Sos.[1]Populasi • Total59,216 (2.010)[2] jiwaKode Kemendagri13.71.08 Kode BPS1371100 Nagari/kelurahan9Situs webpauh.padang.go.id Pauh adalah sebuah kecamatan di kota Padang, Sumatera Barat, Indonesia. Menurut Adat Min...

School 2013Poster promosi untuk School 2013GenreDrama remajaDitulis olehLee Hyun-joo Go Jung-wonSutradaraLee Min-hong Lee Eung-bokPemeranJang NaraChoi DanielLee Jong-sukPark Se-youngNegara asal Korea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduser eksekutifHwang Eui-kyungSinematografiWi Chang-seok[1] Kwon Hyuk-gyunPenyuntingJung Hyun-kyungDurasiSenin dan Selasa 21:55 (KST)Rumah produksiContent K/School SPCRilis asliRilis3 Desember 2012 –28 Januari 2013 School 2013 (Hang...

Swedish multinational retail conglomerate For the city in Nigeria, see Ikeja. Inter IKEA Systems B.V.IKEA store in Conshohocken, PennsylvaniaTrade nameIKEACompany typePrivateIndustryRetailFounded28 July 1943; 80 years ago (1943-07-28)[1] in SwedenFounderIngvar KampradHeadquartersLeiden, NetherlandsNumber of locations462 (2023)[2]Area servedWorldwideKey people Jesper Brodin (Chairman and CEO of INGKA Holding)[3] Jon Abrahamsson Ring (Chairman and CEO o...

Dewan Perwakilan Rakyat Daerah Kabupaten ProbolinggoDewan Perwakilan RakyatKabupaten Probolinggo2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai30 Agustus 2019PimpinanKetuaH. Andi Suryanto Wibowo, S.E., M.M. (NasDem) sejak 26 September 2019 Wakil Ketua ILukman Hakim, S.H., M.Hum. (PKB) sejak 26 September 2019 Wakil Ketua IIOka Mahendra Jati Kusuma, S.E., M.M. (Golkar) sejak 26 September 2019 Wakil Ketua IIIH. Jon Junaidi (Gerindra) sejak 26 September 2...

American politician For the Pennsylvania congressman, see John Hoge. John Blair HogeMember of the U.S. House of Representativesfrom West Virginia's 2nd districtIn officeMarch 4, 1881 – March 3, 1883 Personal detailsBorn(1825-02-02)February 2, 1825Richmond, Virginia, USDiedMarch 1, 1896(1896-03-01) (aged 71)Martinsburg, West Virginia, USPolitical partyDemocraticProfessionJournalist, LawyerMilitary serviceAllegianceConfederate StatesBranch/serviceConfederate States ArmyRankCa...

Zimbabwean long-distance runner Olivia Mugove ChitatePersonal informationBorn (1987-12-07) 7 December 1987 (age 36)SportCountry ZimbabweSportAthleticsEvent5000 metresUpdated on 29 August 2015. Olivia Mugove Chitate (born 7 December 1987) is a long-distance runner from Zimbabwe.[1] She competed in the 5000 metres at the 2015 World Championships in Beijing finishing 24th. International competitions Year Competition Venue Position Event Notes Representing Zimbabwe 2015 Wo...

Pour le jeu, voir sogo. SOGo Informations Développé par Alinto Dernière version (27 septembre 2023) Dépôt github.com/Alinto/sogo Écrit en Objective-C Système d'exploitation Type Unix Environnement GNUstep, GNU/Linux, Solaris, FreeBSD et d'autres variantes du système Unix Langues Multilingue Type Groupware Licence GPL Site web https://sogo.nu/ modifier - modifier le code - voir Wikidata (aide) SOGo est un collecticiel (ou serveur collaboratif) libre dont l'architecture est axée sur l...

2005 GFS Marketplace 400 Race details Race 23 of 36 in the 2005 NASCAR Nextel Cup Series The 2005 GFS Marketplace 400 program cover, featuring Greg Biffle, winner of the 2004 race.Date August 21, 2005Official name 36th Annual GFS Marketplace 400Location Brooklyn, Michigan, Michigan International SpeedwayCourse Permanent racing facility2 mi (3.2 km)Distance 200 laps, 400 mi (643.737 km)Scheduled Distance 200 laps, 400 mi (643.737 km)Average speed 141.551 miles per hour (227.804 km/h)Atten...

Cet article est une ébauche concernant un acteur américain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les conventions filmographiques. Pour les articles homonymes, voir Lou et Ferrigno. Lou Ferrigno Lou Ferrigno en 2019. Données clés Nom de naissance Louis Jude Ferrigno Surnom Big Louie Naissance 9 novembre 1951 (72 ans)Brooklyn, New York (États-Unis) Nationalité Américaine Profession Acteur, culturiste Films notables HerculeThor : Ragn...

Uffheimcomune Uffheim ‚Äì Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementMulhouse CantoneBrunstatt TerritorioCoordinate47¬∞39‚Ä≤N 7¬∞26‚Ä≤E / 47.65¬∞N 7.433333¬∞E47.65; 7.433333Ôªø (Uffheim)Coordinate: 47¬∞39‚Ä≤N 7¬∞26‚Ä≤E / 47.65¬∞N 7.433333¬∞E47.65; 7.433333Ôªø (Uffheim) Superficie4,36 km¬≤ Abitanti907[1] (2009) Densit√Ý208,03 ab./km¬≤ Altre informazioniCod. postale68510 Fuso orarioUTC+1 Codice IN...

„Åì„ÅÆË®ò‰∫ã„ÅØʧúË®ºÂèØËÉΩ„Å™ÂèÇËÄÉÊñáÁåÆ„ÇÑÂá∫ÂÖ∏„ÅåÂÖ®„ÅèÁ§∫„Åï„Çå„Ŷ„ÅÑ„Å™„ÅÑ„Åã„Äʼn∏çÂçÅÂàÜ„Åß„Åô„ÄÇÂá∫ÂÖ∏„ÇíËøΩÂäÝ„Åó„Ŷˮò‰∫ã„ÅƉø°ÈݺÊÄßÂêë‰∏ä„Å´„ÅîÂçîÂäõ„Åè„ÅÝ„Åï„ÅÑ„ÄÇÔºà„Åì„ÅÆ„ÉÜ„É≥„Éó„ɨ„ɺ„Éà„ÅƉΩø„ÅÑÊñπÔºâÂá∫ÂÖ∏ʧúÁ¥¢?: „Ç≥„É´„ÇØ ‚Äì „Éã„É•„ɺ„Çπ ¬∑ Êõ∏Á±ç ¬∑ „Çπ„Ç´„É©„ɺ ¬∑ CiNii ¬∑ J-STAGE ¬∑ NDL ¬∑ dlib.jp ¬∑ „Ç∏„É£„Éë„É≥„ǵ„ɺ„ÉÅ ¬∑ TWLÔºà2017Âπ¥4ÊúàԺ⠄Ç≥„É´„ÇØ„ÇíÊâì„Å°Êäú„ÅфŶ‰Ωú„Å£„ÅüÁì∂„ÅÆÊÝì „Ç≥„É´„ÇØÔºàÊú®ÊÝì„ÄÅÔøΩ...

Ecoregion in India Malabar Coast moist forestsChital (Axis axis) in Sanjay Gandhi National ParkMap of the Malabar Coast moist forests ecoregionEcologyRealmIndomalayanBiometropical and subtropical moist broadleaf forestsBorders List Deccan thorn scrub forestsNorth Western Ghats moist deciduous forestsNorth Western Ghats montane rain forestsSouth Western Ghats moist deciduous forestsSouth Western Ghats montane rain forests GeographyArea34,219 km2 (13,212 sq mi)CountryIndiaStatesG...
2020Âπ¥Â§èÂ≠£Â••ÊûóÂåπÂÖãËøêÂ䮉ºöÊ≥¢ÂÖ∞‰ª£Ë°®ÂúòÊ≥¢ÂÖ∞ÂõΩÊóóIOCÁ∑®Á¢ºPOLNOCÊ≥¢Ëò≠•ßÊûóÂåπÂÖãÂßîÂì°ÊúÉÁ∂≤Á´ôolimpijski.plÔºàËã±ÊñáÔºâÔºàÊ≥¢ÂÖ∞ÊñáÔºâ2020Âπ¥Â§èÂ≠£Â••ÊûóÂåπÂÖãËøêÂ䮉ºöÔºàÊù±‰∫¨Ôºâ2021Âπ¥7Êúà23Êó•Ëá≥8Êúà8Êó•ÔºàÂèó2019ÂÜÝÁä∂ÁóÖÊØíÁóÖÁñ´ÊÉÖÂΩ±ÂìçÊé®ËøüÔºå‰Ω܉ªç‰øùÁïôÂéüÂÆöÂêçÁß∞ÔºâÈÅãÂãïÂì°206ÂèÉË≥ΩÈÝÖÁõÆ24‰∏™Â§ßÈ°πÊóóÊâãºÄÂπïºèÔºöÂ∏ïÁª¥Â∞î¬∑ÁßëÁÉ≠Â∞ºÂ••Â§´ÊñØÂü∫ÔºàÊ∏∏Ê≥≥ÔºâÂíåÈ©¨Â®Ö¬∑Ê≤ɉªÄ‰πÊñØÂç°ÔºàËá™Ë°åËΩ¶Ôºâ[1]Èó≠ÂπïºèÔºöÂç°ÁΩóÂà©Â®ú¬∑Á∫≥‰∫öÔºàÁöÆÂàíËâáÔºâ&#...

Sisi lain dari Bunaken Taman laut Bunaken dilihat dari dalam perahu katamaran Taman laut Bunaken dilihat dari dalam perahu katamaran Bunaken adalah sebuah pulau seluas 8,08 km² di Teluk Manado, yang terletak di utara pulau Sulawesi, Indonesia. Pulau ini merupakan bagian dari kota Manado, ibu kota provinsi Sulawesi Utara, Indonesia. Pulau Bunaken dapat di tempuh dengan kapal cepat (speed boat) atau kapal sewaan dengan perjalanan sekitar 30 menit dari pelabuhan kota Manado. Di sekitar pul...

–ß–∞—Å—Ç–∏–Ω–∞ —Å–µ—Ä—ñ—ó –ø—Ä–æ–§—ñ–ª–æ—Å–æ—Ñ—ñ—èLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, Averroes–ü–ª–∞—Ç–æ–Ω–ö–∞–Ω—Ç–ù—ñ—Ü—à–µ–ë—É–¥–¥–∞–ö–æ–Ω—Ñ—É—Ü—ñ–π–ê–≤–µ—Ä—Ä–æ–µ—Å –§—ñ–ª–æ—Å–æ—Ñ–∏ –ï–ø—ñ—Å—Ç–µ–º–æ–ª–æ–≥–∏ –ï—Å—Ç–µ—Ç–∏–∫–∏ –ï—Ç–∏–∫–∏ –õ–æ–≥—ñ–∫–∏ –ú–µ—Ç–∞—Ñ—ñ–∑–∏–∫–∏ –°–æ—Ü—ñ–∞–ª—å–Ω–æ-–ø–æ–ª—ñ—Ç–∏—á–Ω—ñ —Ñ—ñ–ª–æ—Å–æ—Ñ–∏ –¢—Ä–∞–¥–∏—Ü—ñ—ó –ê–Ω–∞–ª—ñ—Ç–∏—á–Ω–∞ –ê—Ä—ñ—Å—Ç–æ—Ç–µ–ª—ñ–≤—Å—å–∫–∞ –ê—Ñ—Ä–∏–∫–∞–Ω—Å—å–∫–∞ –ë–ª–∏–∑—å–∫–æ—Å—Ö—ñ–¥–Ω–∞ —ñ—Ä–∞–Ω—Å—å–∫–∞ –ë—É–¥–¥—ñ–πÔøΩ...

Pour les articles homonymes, voir Artaxias et Ardach√®s. Artaxias IV Titre Roi d'Arm√©nie 423 ‚Äì 428(5 ans) Pr√©d√©cesseur Vram Ch√¢hpouh, suivi d'un interr√®gne Successeur (abolition de la monarchie ; Veh Mihr Chapour, marzb√¢n) Biographie Dynastie Arsacides P√®re Vram Ch√¢hpouh M√®re Varazdoukht modifier Artaxias ou Artach√®s IV d'Arm√©nie (en arm√©nien ‘±÷Ä’ø’°’∑’•’Ω ‘¥) est le dernier roi arsacide d'Arm√©nie, de 423 √Ý 428. Biographie Artach√®s IV est le fils du roi Vram...

–£ –í—ñ–∫—ñ–ø–µ–¥—ñ—ó —î —Å—Ç–∞—Ç—Ç—ñ –ø—Ä–æ —ñ–Ω—à—ñ –Ω–∞—Å–µ–ª–µ–Ω—ñ –ø—É–Ω–∫—Ç–∏ –∑ —Ç–∞–∫–æ—é –Ω–∞–∑–≤–æ—é: –ó–∞–≥—ñ—Ä'—è. —Å–µ–ª–æ –ó–∞–≥—ñ—Ä'—è –ì–µ—Ä–± –ó–∞–≥—ñ—Ä'—è –ü—Ä–∞–ø–æ—Ä –ó–∞–≥—ñ—Ä'—è –ö—Ä–∞—ó–Ω–∞ –£–∫—Ä–∞—ó–Ω–∞ –û–±–ª–∞—Å—Ç—å –Ü–≤–∞–Ω–æ-–§—Ä–∞–Ω–∫—ñ–≤—Å—å–∫–∞ –æ–±–ª–∞—Å—Ç—å –Ý–∞–π–æ–Ω –Ü–≤–∞–Ω–æ-–§—Ä–∞–Ω–∫—ñ–≤—Å—å–∫–∏–π —Ä–∞–π–æ–Ω –ì—Ä–æ–º–∞–¥–∞ –Ý–æ–≥–∞—Ç–∏–Ω—Å—å–∫–∞ –º—ñ—Å—å–∫–∞ –≥—Ä–æ–º–∞–¥–∞ –û—Å–Ω–æ–≤–Ω—ñ –¥–∞–Ω—ñ –ü–µ—Ä—à–∞ –∑–≥–∞–¥–∫–∞ 2 —Å—ñ—á–Ω—è 1441[1]...















![{\displaystyle {\begin{aligned}\prod _{p\in P}\sum _{k\geq 0}{\frac {1}{p^{k}}}&=\sum _{k\geq 0}{\frac {1}{2^{k}}}\times \sum _{k\geq 0}{\frac {1}{3^{k}}}\times \sum _{k\geq 0}{\frac {1}{5^{k}}}\times \sum _{k\geq 0}{\frac {1}{7^{k}}}\times \cdots \\[8pt]&=\sum _{k,\ell ,m,n,\cdots \geq 0}{\frac {1}{2^{k}3^{\ell }5^{m}7^{n}\cdots }}=\sum _{n}{\frac {1}{n}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a03346c59f44f9910104cbd6c74bf685073927)















![{\displaystyle {\begin{aligned}1+\sum _{i}\left[{\frac {x}{p_{i}}}\right]-\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor &+\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor -\cdots \\&\cdots \pm (-1)^{N+1}\left\lfloor {\frac {x}{p_{1}\cdots p_{N}}}\right\rfloor .\qquad (1)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/816a9cae28e981791439422b8df881604d5dd4ab)



























