平方数
|
Read other articles:

Artikel ini tentang tahun 2015. 2015MileniumMilenium ke-3AbadAbad ke-20Abad ke-21 Abad ke-22Dasawarsa 1990-an2000-an2010-an2020-an2030-anTahun2012201320142015201620172018 2015 (MMXV) merupakan tahun biasa yang diawali hari Kamis dalam kalender Gregorian, tahun ke-2015 dalam sebutan Masehi (CE) dan Anno Domini (AD), tahun ke-15 pada Milenium ke-3, tahun ke-15 pada Abad ke-21, dan tahun ke- 6 pada dekade 2010-an. Denominasi 2015 untuk tahun ini telah digunakan sejak periode Abad Pertengaha...
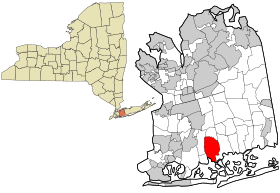
لمعانٍ أخرى، طالع فريبورت (توضيح). فريبورت الإحداثيات 40°39′14″N 73°35′13″W / 40.6539°N 73.5869°W / 40.6539; -73.5869 [1] تاريخ التأسيس 1892 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة ناسو خصائص جغرافية المساحة 4.8 ميل مر...

Kabinet DaruratKabinet Pemerintahan IndonesiaRumah ketua PDRI Sjafroedin Prawiranegara di Bidar Alam yang dipergunakan juga untuk kantor pemerintahanDibentuk19 Desember 1948Diselesaikan13 Juli 1949Struktur pemerintahanKepala negaraSukarnoKepala pemerintahanSyafruddin PrawiranegaraSejarahPendahuluKabinet Hatta IPenggantiKabinet Hatta II Artikel ini bagian dariseri tentangSoekarno Presiden pertama Indonesia Prakemerdekaan PNI Partindo PETA BPUPK Pancasila PPKI Revolusi Nasional Indonesia Prokla...

مكتب تنسيق القبول في الجامعات المصريةالإطارالنوع مؤسسة حكومية المقر الرئيسي القاهرة البلد مصر تعديل - تعديل مصدري - تعديل ويكي بيانات مكتب تنسيق القبول في الجامعات المصرية هو الجهة المنوط بها استقبال رغبات الطلاب المصريين الحاصلين علي شهادة الثانوية العامة أو شهادة ا�...
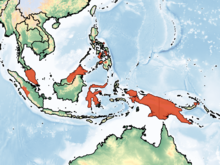
Species of vesper bat Rohu's bat Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Chiroptera Family: Vespertilionidae Genus: PhiletorThomas, 1902 Species: P. brachypterus Binomial name Philetor brachypterus(Temminck, 1840) Rohu's bat (Philetor brachypterus) is a species of vesper bat. It is the only species in the genus Philetor. It is found in Brunei, Indonesia, Malaysia, N...

Mappa della Central London. Il termine Central London (Londra Centrale in italiano) si riferisce a quella parte di Londra che è vicina al nucleo centrale della città. Benché non vi sia una definizione convenzionale né ufficiale che definisca questa zona, sono le caratteristiche di questa, ossia l'alta densità abitativa, gli elevati valori dei terreni, l'elevata popolazione diurna e l'alta concentrazione di organizzazioni rilevanti a livello regionale, nazionale e internazionale, a defini...

American navigation satellite used for GPS USA-132A Block IIR GPS satelliteNamesNavstar 43GPS IIR-2GPS SVN-43Mission typeNavigationOperatorU.S. Air ForceCOSPAR ID1997-035A [1]SATCAT no.24876Mission duration10 years (planned) 26 years, 7 months and 18 days (elapsed) Spacecraft propertiesSpacecraftGPS IIRSpacecraft typeGPS Block IIR[2]BusAS-4000ManufacturerLockheed MartinLaunch mass2,032 kg (4,480 lb) Start of missionLaunch date23 July 1997, 03:43:01 UTC...

British environmentalist, writer and philosopher For the Irish Anglican priest, see Edward Goldsmith (priest). This article may contain excessive or inappropriate references to self-published sources. Please help improve it by removing references to unreliable sources where they are used inappropriately. (June 2022) (Learn how and when to remove this template message) Edward GoldsmithBornEdward René David Goldsmith(1928-11-08)8 November 1928Paris, FranceDied21 August 2009(2009-08-21) (aged&#...

Austrian actress (born 1980) This biography of a living person relies on a single source. You can help by adding reliable sources to this article. Contentious material about living people that is unsourced or poorly sourced must be removed immediately. (September 2015) (Learn how and when to remove this template message) Franziska WeiszFranziska Weisz, Berlinale 2020Born (1980-05-04) 4 May 1980 (age 43)Vienna, AustriaNationalityAustrianOccupationActressYears active2001–presentSpou...

Academic journalCentral Asian SurveyDisciplineCentral Asian studiesLanguageEnglishEdited byRico Isaacs/Alexander MorrisonPublication detailsHistory1982-presentPublisherRoutledgeFrequencyQuarterlyStandard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )ISO 4Cent. Asian Surv.IndexingCODEN (alt · alt2) · JSTOR (alt) · LCCN (alt)MIAR · NLM (alt) · Scop...

Davide Astori Astori con la nazionale italiana nel 2015 Nazionalità Italia Altezza 189 cm Peso 80 kg Calcio Ruolo Difensore CarrieraGiovanili 1995-1999 San Pellegrino1999-2001 Ponte San Pietro2001-2005 MilanSquadre di club1 2005-2006 Milan0 (0)2006-2007→ Pizzighettone25 (1)[1]2007-2008→ Cremonese31 (0)[2]2008-2014 Cagliari174 (3)2014-2015→ Roma24 (1)2015-2018 Fiorentina91 (3)Nazionale 2004-2005 Italia U-184 (0)2011-2017 ...

Peter Graves Peter Graves, pseudonimo di Peter Aurness (Minneapolis, 18 marzo 1926 – Los Angeles, 14 marzo 2010[1]), è stato un attore e regista statunitense. Indice 1 Carriera 2 Filmografia parziale 2.1 Cinema 2.2 Film d'animazione 2.3 Televisione 3 Doppiatori italiani 4 Note 5 Altri progetti 6 Collegamenti esterni Carriera Fratello dell'attore James Arness, è principalmente conosciuto per la sua interpretazione di Jim Newton, il padre adottivo di Joey, nella serie televisiva di ...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

1928 film The Woman DisputedTheatrical posterDirected byHenry King, Sam TaylorWritten byC. Gardner SullivanProduced byJoseph M. Schenck ProductionsDistributed byUnited ArtistsRelease date September 1928 (1928-09) Running time108 minutesCountryUnited StatesLanguageSound film (Synchronized) The Woman Disputed is a 1928 American synchronized sound film. While the film has no audible dialog, it was released with a synchronized musical score with sound effects using both the sound-on-dis...

Unincorporated town in the State of Nevada, United States Census-designated place and unincorporated town in Nevada, United StatesWinchester, NevadaCensus-designated place and unincorporated townSahara Hotel Station of the monorailLocation of Winchester in Clark County, NevadaCoordinates: 36°8′9″N 115°7′15″W / 36.13583°N 115.12083°W / 36.13583; -115.12083CountryUnited StatesStateNevadaCountyClarkFoundedApril 23, 1951; 73 years ago (1951-0...

الدوري البولندي الممتاز 2017–18 تفاصيل الموسم الدوري البولندي الممتاز النسخة 92 البلد بولندا التاريخ بداية:14 يوليو 2017 نهاية:20 مايو 2018 المنظم اتحاد بولندا لكرة القدم البطل ليغيا وارسو[1] الهابطون نيتشيتشا مباريات ملعوبة 296 عدد المشاركين 16 ...

توبيلوحة ألبرت إيكهوت للتوبيالتعداد الكليالتعداد 11،000،000 (تاريخياً) ، بونتيغوارا 10،837 ، توبينامبا دي أوليفينسا 3،000 ، توبينيكيم 2،630 ، انقرضت قبائل آخرون لكن أسلافهم سكان باردو ومستيزو البرازيليينمناطق الوجود المميزة وسط وساحل البرازيل وسط وساحل البرازيلاللغات لغات توبي ،...

Anti-war protest in London, UK Brian Haw and Barbara Tucker at the Parliament Square Peace Campaign site, in August 2010 The Parliament Square Peace Campaign was a peace camp outside the Palace of Westminster in Parliament Square, London, from 2001 to 2013.[1] Activist Brian Haw launched the campaign at the site on 2 June 2001, initially as an around-the-clock protest in response to the United Nations economic sanctions imposed on Iraq.[2] His protest grew broader following th...

List of minerals with Wikipedia articles This is a list of minerals which have Wikipedia articles. Minerals are distinguished by various chemical and physical properties. Differences in chemical composition and crystal structure distinguish the various species. Within a mineral species there may be variation in physical properties or minor amounts of impurities that are recognized by mineralogists or wider society as a mineral variety. Mineral variety names are listed after the valid minerals...

Pour les articles homonymes, voir Écho et Échos (série télévisée). Échos/Echoes Album de Anggun Sortie 7 novembre 2011 Durée 58:32 (France) Genre Pop Producteur Anggun Label April Earth, Warner Music France, Sony Music Classement 1er en Indonésie Albums de Anggun Élévation(2008) Toujours un ailleurs(2015)Singles Je partirai (France)Sortie : 1er juin 2011 Always You (International)Sortie : 9 juin 2011 Mon Meilleur Amour / Only Love / Hanyalah Cinta (Mondial)Sort...






![{\displaystyle n(n+1)(n+2)(n+3)+1=(n^{2}+3n+1)^{2}=[n+(n+1)^{2}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aec4b311a9c21dfc77ebac3f703ce22a35aa127)


