Часткова похідна
|
Read other articles:

2019 mayoral election in South Bend, Indiana 2019 South Bend mayoral election ← 2015 November 5, 2019 2023 → Turnout15% Nominee James Mueller Sean M. Haas Party Democratic Republican Popular vote 9,437 5,445 Percentage 63.41% 36.58% Results by Common Council district Mayor before election Pete Buttigieg Democratic Elected Mayor James Mueller Democratic Elections in Indiana Federal government Presidential elections 1816 1820 1824 1828 1832 1836 1840 1844 1848 ...

Town in Newfoundland and Labrador, CanadaAppletonTownMotto: Room to GrowAppletonLocation of Appleton in NewfoundlandCoordinates: 48°59′08″N 54°51′53″W / 48.98556°N 54.86472°W / 48.98556; -54.86472Country CanadaProvince Newfoundland and LabradorCensus division6IncorporatedFebruary 27, 1962Government • MayorGarret WattonArea • Land6.39 km2 (2.47 sq mi)Population (2021) • Total620Time zone...

2018 video game 2018 video gameDarksiders IIIDeveloper(s)Gunfire GamesPublisher(s)THQ NordicDirector(s)David AdamsProducer(s)Reinhard PolliceDesigner(s)James BeechNicolas FikacMarcus Luna DeLeonCindy ToRichard VorodiWriter(s)Man of ActionComposer(s)Cris VelascoSeriesDarksidersEngineUnreal Engine 4[1]Platform(s) PlayStation 4 Windows Xbox One Stadia Nintendo Switch ReleasePlayStation 4, Windows, Xbox OneNovember 27, 2018StadiaSeptember 14, 2021Nintendo SwitchSeptember 30, 2021Genre(s)A...

منطقة عين العرب موقع منطقة عين العرب في محافظة حلب تقسيم إداري البلد سوريا[1] العاصمة عين العرب المحافظة محافظة حلب المسؤولون المنطقة منطقة عين العرب المركز عين العرب رمز المنطقة SY0206 خصائص جغرافية إحداثيات 36°53′N 38°22′E / 36.89°N 38.37°E / 36.89; 38.37 المساح�...

1978 filmSpider-Man Strikes BackBritish theatrical release posterDirected byRon SatlofScreenplay byRobert Janes[1]Based onSpider-Man[1]Produced by Ran Satlof Robert Janes[1] Starring Nicholas Hammond Joanna Cameron Robert F. Simon Michael Pataki CinematographyJack Whitman[1]ProductioncompanyCharles Fries Productions[1]Distributed byColumbia Pictures Television (United States)Columbia Pictures (International)Release datesMay 8, 1978 (Europe)December 21, ...

Questa voce o sezione sull'argomento fumettisti statunitensi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sull'argomento fumettisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Sergio Aragonés nel 2017 Sergio Aragonés Domenech (San Mateo, 6 settembre 1937) è un fumettista e scritt...

KreyoDesaNegara IndonesiaProvinsiJawa BaratKabupatenCirebonKecamatanKlangenanKode Kemendagri32.09.23.2011 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Kreyo adalah desa di kecamatan Klangenan, Cirebon, Jawa Barat, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia) Peraturan Menteri Dalam Negeri Nomor 72 Tahun 2019 tentang ...

Ghost RiderMarvel Spotlight (vol. 1) n. 5 sulla copertina Marvel Collection Special presenta Ghost Rider, disegnato da Mike Ploog UniversoUniverso Marvel Lingua orig.Inglese AutoriRoy Thomas Gary Friedrich Mike Ploog EditoreMarvel Comics 1ª app.agosto 1972 1ª app. inMarvel Spotlight (vol. 1[1]) n. 5 Editore it.Editoriale Corno 1ª app. it.maggio 1979 1ª app. it. inDevil n. 105 Caratteristiche immaginarieAlter ego Phantom Rider (Carter Slade) Noble Kale Johnny ...

RMS RepublicDescrizione generale TipoTransatlantico Armatore Dominion Line (1903) White Star Line (1903-1909) ProprietàDominion Line (1903)White Star Line (1903-1909) Porto di registrazioneLiverpool IdentificazioneIndicativo di chiamata radio ITU:VFPK(Victor-Foxtrot-Papa-Kilo) Numero ufficiale del Regno Unito: 118043 Impostazione1902 Varo26 febbraio 1903 Entrata in servizio12 settembre 1903 Nomi precedentiColumbus (1903) Destino finaleSperonato ed affondato al largo di Nantucket il 24 gennai...

Magazine published by fans British punk and post-punk fanzines from the 1970s A fanzine (blend of fan and magazine or -zine) is a non-professional and non-official publication produced by enthusiasts of a particular cultural phenomenon (such as a literary or musical genre) for the pleasure of others who share their interest. The term was coined in an October 1940 science fiction fanzine by Russ Chauvenet and first popularized within science fiction fandom, and from there the term was adopted ...
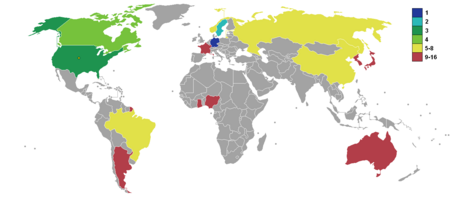
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Piala Dunia Wanita FIFA 2003 – berita · surat kabar · buku · cendekiawan · JSTOR Piala Dunia Wanita FIFA 20032003 FIFA Women's World Cup (Bhs. Inggris) Logo resmi Piala Dunia Wanita FIFA 2003Informasi turname...

Former political party in the Dutch East Indies Indonesian Islamic Party Partai Islam IndonesiaAbbreviationPIILeaderSoekiman WirjosandjojoFounded4 December 1938 (1938-12-04)Dissolvedc. March 1942 (1942-03)Split fromIndonesian Islamic Union Party (PSII)IdeologyIslamic socialismNational affiliationIndonesian Political Federation (GAPI) The Indonesian Islamic Party (Indonesian: Partai Islam Indonesia, PII) was an Islamic political party in the Dutch East Indies (now...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: First Battle of Tuxpan – news · newspapers · books · scholar · JSTOR (July 2015) First Battle of TuxpanPart of Mexican–American WarThe U.S. naval expedition under Commodore M. C. Perry, ascending the Tuspan River; destroying the forts, and taking po...

Disambiguazione – Se stai cercando altri significati, vedi Marco Claudio Marcello (disambigua). Marco Claudio MarcelloConsole della Repubblica romanaDenario con l'effige di Marco Claudio Marcello (I sec. a.C.) in un conio celebrativo curato da un discendente di Marcello, per ricordare la conquista della Sicilia (a questo allude il triscele a sinistra), avvenuta nel 212-210 a.C.[1] Nome originaleMarcus Claudius Marcellus Nascitaante 268 a.C. Morte208 a.C.[2]Venosa Figli...

Moisdon-la-Rivière L'église Saint Jouin. Blason Administration Pays France Région Pays de la Loire Département Loire-Atlantique Arrondissement Châteaubriant-Ancenis Intercommunalité Communauté de communes Châteaubriant-Derval Maire Mandat Patrick Galivel 2020-2026 Code postal 44520 Code commune 44099 Démographie Gentilé Moisdonnais Populationmunicipale 1 962 hab. (2021 ) Densité 39 hab./km2 Géographie Coordonnées 47° 37′ 20″ nord, 1° 22�...

David pada 2021 David Darryl Wilson (bahasa Tamil: டேரல் டேவிட் Ṭēral Tēviṭ; kelahiran 1970),[1] yang lebih dikenal sebagai Darryl David, adalah seorang politikus dan mantan penyiar media Singapura. Sebagai anggota Partai Aksi Rakyat, ia menjadi anggota Parlemen ke-14 sejak 2015.[2][3] David juga menjadi kepala jabatan eksekutif SJI International School.[4] Referensi ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemu...

Cesare SforzaMaestro della Pala Sforzesca, particolare della Pala Sforzesca, presunto ritratto di Cesare Sforza del 1494-95NobiluomoStemma NascitaMilano, 3 maggio 1491 MorteMilano, 4 gennaio 1514 (22 anni) DinastiaSforza PadreLudovico Maria Sforza MadreCecilia Gallerani ReligioneCattolicesimo Ducato di MilanoCasato degli Sforza Francesco I Figli Galeazzo Maria Ippolita Maria Filippo Maria Sforza Maria Ludovico Maria Elisabetta Maria Ascanio Maria Ottaviano Maria Fiordelisa Maria Sf...

Capability that can be built into web servers and web clients HTTP Persistence Compression HTTPS QUIC Request methods OPTIONS GET HEAD POST PUT DELETE TRACE CONNECT PATCH Header fields Cookie ETag Location HTTP referer DNT X-Forwarded-For Response status codes 301 Moved Permanently 302 Found 303 See Other 403 Forbidden 404 Not Found 451 Unavailable for Legal Reasons Security access control methods Basic access authentication Digest access authentication Security vulnerabilities HTTP header in...

DiplocaulusRentang fosil: 306–255 jtyl PreЄ Є O S D C P T J K Pg N Karbon Akhir sampai Permian Akhir Model rekonstruksi kerangka dan restorasi hidup Diplocaulus di Denver Museum of Nature and Science Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Subkelas: †Lepospondyli Ordo: †Nectridea Famili: †Diplocaulidae Genus: †DiplocaulusCope, 1877 Spesies tipe * †D. salamandroidesCope, 1877 Spesies lain †D. magnicornis Cope, 1882 †D. brevirostris Olson, 1951 †D. recurv...

For other uses, see Basra (disambiguation). Basrah redirects here. For the village in eastern Yemen, see Basrah, Yemen. Not to be confused with Bosra, Busra al-Harir, or Bozrah. Metropolis in IraqBasra ٱلْبَصْرَةBasrahMetropolisNickname: Venice of the East[1]BasraLocation of Basra within IraqShow map of IraqBasraBasra (Near East)Show map of Near EastCoordinates: 30°30′54″N 47°48′36″E / 30.51500°N 47.81000°E / 30.51500; 47.81000Country...




































