–†—Г–і–љ—П (–Ф—Г–±–µ–љ—Б—М–Ї–Є–є —А–∞–є–Њ–љ)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:
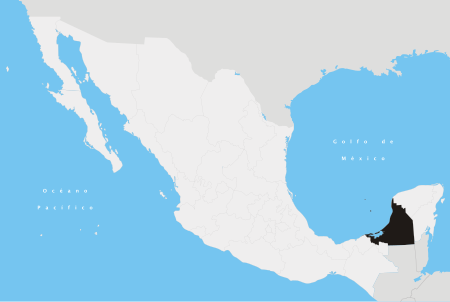
Ciudad del Carmen adalah sebuah kota di barat daya negara bagian Campeche, Meksiko. Ciudad del Carmen terletak di 18¬∞38вА≤N 91¬∞50вА≤W / 18.63¬∞N 91.83¬∞W / 18.63; -91.83 di barat daya Pulau Carmen, yang terbentang di Laguna de T√©rminos di pantai Teluk Meksiko. Referensi Link to tables of population data from Census of 2005 Instituto Nacional de Estad√≠stica, Geograf√≠a e Inform√°tica (INEGI) [1] Pranala luar Wikimedia Commons memiliki media mengenai Ciudad del Carme...

Webtoon hosting service WEBTOON redirects here. For the comic format, see Webtoon. WebtoonType of siteWebtoon platformAvailable inMultilingualOwner Naver Corporation (66.8%) LY Corporation (33.3%) Created byJunKoo KimParentWebtoon EntertainmentURLKorean websiteEnglish websiteCommercialYesRegistrationOptionalLaunched 2004 Korean 2013 Japanese (Line Manga launched) 2014 English, Thai, Mandarin, Cantonese 2015 Indonesian 2019 Spanish, French Current statusActive Webtoon[a]...

Ford Motor CompanyJenisPerusahaan publik (NYSE: F)IndustriOtomotifDidirikan16 Juni 1903PendiriHenry FordKantorpusatDearborn, Michigan, Amerika SerikatWilayah operasiSeluruh duniaTokohkunciWilliam C. Ford, Jr.(Executive Chairman)Alan R. Mulally(President & CEO)ProdukMobilSuku cadang kendaraanPendapatan US$146,91 milyar (2013)[1]Laba operasi US$5,42 milyar (2013)[1]Laba bersih US$7,15 milyar (2013)[1]Total aset US$202,02 milyar (2013)[1]Total ekuitas US$26,38...

Negosiasi dalam Perjanjian Portsmouth (1905) Perjanjian Portsmouth adalah perjanjian yang mengakhiri Perang Rusia-Jepang pada tahun 1905.[1] Perjanjian ini ditandatangani di pangkalan angkatan laut Portsmouth, New Hampshire dengan perantara Theodore Roosevelt.[1] Dalam perjanjian ini, Jepang mendapat jaminan pengunduran diri tentara Rusia dari Manchuria Selatan yang terdiri dari penyerahan jaringan kereta api Manchuria, pelepasan kedudukan khusus Rusia Korea dan hak kontrak se...

Tamamo-no-Mae. Cetakan oleh Yoshitoshi. Sessho-seki di Nasu, Tochigi Tamamo-no-Mae (зОЙиЧїеЙН atau зОЙиЧїгБЃеЙН, зОЙиЧїеЊ°еЙНcode: ja is deprecated ) adalah tokoh legendaris dalam mitologi dan cerita rakyat Jepang. Dalam Otogizoshi, kumpulan prosa Jepang ditulis selama periode Muromachi, Tamamo-no-Mae diceritakan sebagai selir Kaisar Konoe yang bertahta dari tahun 1142 hingga 1155. Ia dikatakan sebagai wanita paling cantik dan pintar di Jepang. Tubuh Tamamo-no-Mae secara misterius mengeluarka...

Microbiotheria southern monito del monte (en) TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoMicrobiotheria Ameghino, 1889 Famili Microbiotheriidae lbs Microbiotheria adalah ordo marsupialia australidelphia yang meliputi satu keluarga (Microbiotheriidae), satu genus (Dromiciops), dan satu spesies (D. gliroides).[1] Sejumlah spesies telah punah yang diketahui dari fosil di Amerika Selatan, Antarktika Barat, dan timur laut Australia.[2] Referensi ^ ADW: Microbiotheria. A...

ињљжЩЙйЩЄиїНдЇМзіЪдЄКе∞ЗиґЩ側驧е∞ЗиїНдЄ™дЇЇиµДжЦЩеЗЇзФЯ1910еєі е§ІжЄЕж≤≥еНЧзЬБи°ЫиЉЭеЇЬж±≤зЄ£йАЭдЄЦ1958еєі8жЬИ23жЧ•(1958ж≠≤вАФ08вАФ23)пЉИ47вАФ48ж≠≤пЉЙ † дЄ≠иПѓж∞СеЬЛз¶ПеїЇзЬБйЗСйЦАзЄ£еЫљз±Н дЄ≠иПѓж∞СеЬЛжФњеЕЪ дЄ≠еЬЛеЬЛж∞Сйї®иОЈе•Ц йЭТ姩зЩљжЧ•еЛ≥зЂ†пЉИињљиіИпЉЙеЖЫдЇЛиГМжЩѓжХИењ† дЄ≠иПѓж∞СеЬЛжЬНељє еЬЛж∞СйЭ©еСљиїН дЄ≠иПѓж∞СеЬЛйЩЄиїНжЬНељєжЧґйЧі1924еєіпЉН1958еєіеЖЫи°Ф дЇМзіЪдЄКе∞З пЉИињљжЩЙпЉЙйГ®йШЯеЫЫеНБдЄГеЄЂжМЗжМ•жЭ±еМЧеЙњеМ™зЄљеПЄдї§йГ®еПГиђАйХЈйЩЄиїНпњљ...

Keling (dari bahasa Sanskerta: Kalingga) adalah sebuah daerah di India Selatan. Kata ini bisa pula merujuk kepada suatu suku bangsa Dravida atau Tamil yang berasal dari sana.[butuh rujukan] Juga berdirinya Kerajaan Kalingga (Holing) yang dirajai Ratu Sima, pada abad ke 7 di Indonesia.[1] Selain itu Keling juga merupakan nama wilayah yang sekarang menjadi desa Keling di Kediri. Sehingga menurut pendapat sejarawan, Keling bukan merujuk kepada wilayah di India melainkan wilayah b...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Movie Love вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (April 2022) (Learn how and when to remove this message) First edition (publ. E. P. Dutton) Movie Love: Complete Reviews 1988вАУ1991 (1991) is the 11th and last collection of film reviews by the critic Pa...

My Little Pony: Friendship is MagicMusim 1Sampul DVDNegara asal Amerika Serikat Kanada Jml. episode26RilisJaringan asliThe HubTanggal disiarkan10 Oktober 2010 (2010-10-10) вАУ6 Mei 2011 (2011-5-6)Kronologi MusimBerikutnya вЖТMusim 2Daftar episode Musim pertama dari serial televisi animasi My Little Pony: Friendship Is Magic, dikembangkan oleh Lauren Faust, awalnya ditayangkan di The Hub di Amerika Serikat. Serial ini didasarkan pada lini mainan dan karya animasi My Little ...

2014 soundtrack album by Alexandre Desplat The Grand Budapest Hotel: Original SoundtrackSoundtrack album by Alexandre DesplatReleasedMarch 4, 2014StudioAir StudiosAbbey Road Studios (London) Studio Guillaume Tell (Paris)GenreSoundtrackLength59:50LabelABKCOProducer Wes Anderson Randall Poster Wes Anderson film soundtrack chronology Moonrise Kingdom (Original Soundtrack)(2012) The Grand Budapest Hotel: Original Soundtrack(2014) Isle of Dogs: Original Soundtrack(2018) The Grand Budapest Hote...

Ў™Ў≠Ў™ЎІЎђ ўЗЎ∞ўЗ ЎІўДўЕўВЎІўДЎ© ўГЎІўЕўДЎ©ўЛ Ў£ўИ Ў£ЎђЎ≤ЎІЎ°ўЛ ўЕўЖўЗЎІ Ў•ўДўЙ Ў™ЎѓўВўКўВ ўДЎЇўИўК Ў£ўИ ўЖЎ≠ўИўК. ўБЎґўДўЛЎІ Ў≥ЎІўЗўЕ ўБўК Ў™Ў≠Ў≥ўКўЖўЗЎІ ўЕўЖ ЎЃўДЎІўД ЎІўДЎµўКЎІўЖЎ© ЎІўДўДЎЇўИўКЎ© ўИЎІўДўЖЎ≠ўИўКЎ© ЎІўДўЕўЖЎІЎ≥Ў®Ў©.Learn how and when to remove this message ЎЇЎ≤ўЖЎ© ЎЇЎ≤ўЖўК ўЕЎѓўКўЖЎ© ЎЇЎ≤ўЖЎ© ЎІўДўВЎѓўКўЕЎ©ўЕЎѓўКўЖЎ© ЎЇЎ≤ўЖЎ© ЎІўДўВЎѓўКўЕЎ© Ў™ўВЎ≥ўКўЕ Ў•ЎѓЎІЎ±ўК ЎІўДЎ®ўДЎѓ Ў£ўБЎЇЎІўЖЎ≥Ў™ЎІўЖ [1] ЎєЎІЎµўЕЎ© ўДўА ЎІўДЎѓўИўДЎ© ЎІўДЎЇЎ≤ўЖўИўКЎ©ўЕўЖЎЈўВЎ© ЎЇ...

–І–∞—Б—В–Є–љ–∞ —Б–µ—А—Ц—Ч –њ—А–Њ–§—Ц–ї–Њ—Б–Њ—Д—Ц—ПLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, Averroes–Я–ї–∞—В–Њ–љ–Ъ–∞–љ—В–Э—Ц—Ж—И–µ–С—Г–і–і–∞–Ъ–Њ–љ—Д—Г—Ж—Ц–є–Р–≤–µ—А—А–Њ–µ—Б –§—Ц–ї–Њ—Б–Њ—Д–Є –Х–њ—Ц—Б—В–µ–Љ–Њ–ї–Њ–≥–Є –Х—Б—В–µ—В–Є–Ї–Є –Х—В–Є–Ї–Є –Ы–Њ–≥—Ц–Ї–Є –Ь–µ—В–∞—Д—Ц–Ј–Є–Ї–Є –°–Њ—Ж—Ц–∞–ї—М–љ–Њ-–њ–Њ–ї—Ц—В–Є—З–љ—Ц —Д—Ц–ї–Њ—Б–Њ—Д–Є –Ґ—А–∞–і–Є—Ж—Ц—Ч –Р–љ–∞–ї—Ц—В–Є—З–љ–∞ –Р—А—Ц—Б—В–Њ—В–µ–ї—Ц–≤—Б—М–Ї–∞ –Р—Д—А–Є–Ї–∞–љ—Б—М–Ї–∞ –С–ї–Є–Ј—М–Ї–Њ—Б—Е—Ц–і–љ–∞ —Ц—А–∞–љ—Б—М–Ї–∞ –С—Г–і–і—Ц–єпњљ...

83rd Regiment or 83rd Infantry Regiment may refer to: Royal Irish Regiment (1992), a unit of the British Army which carries on the lineage of the 83rd Ulster Defense Regiment 83rd Regiment of Foot (disambiguation), several units of the British Army 83rd Wallajahbad Light Infantry, a unit of the British Indian Army 83rd Field Artillery Regiment, United States 83rd Fighter Aviation Regiment, later Fighter-Bomber regiment, a unit of the Yugoslav Air Force American Civil War regiments: 83rd Illin...

This article is part of a series on thePolitics of Switzerland Constitution Human rights Federal Council Members (by seniority) Beat Jans Guy Parmelin Ignazio Cassis Viola Amherd (President) Karin Keller-Sutter (Vice President) Albert R√ґsti √Йlisabeth Baume-Schneider Federal Chancellor Viktor Rossi Federal administration Federal Assembly Council of States (members) National Council (members) Political parties Elections Voting Elections 1848 1851 1854 1857 1860 1863 1866 1869 1872 1875 1878 ...

British politician (born 1965) The subject of this article is standing for re-election to the House of Commons of the United Kingdom on 4 July, and has not been an incumbent MP since Parliament was dissolved on 30 May. Some parts of this article may be out of date during this period. Please feel free to improve this article (but note that updates without valid and reliable references will be removed) or discuss changes on the talk page. The Right HonourableGreg HandsOfficial portrai...

Central channel that controls other constituent radios This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Control channel вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (September 2014) (Learn how and when to remove this message) A Cellular network tower in the Philippines.In radio communication, a control chann...

Politics of Mexico Federal government Constitution of Mexico(history) Human rights LGBT rights Law Abortion Labor Nationality Capital punishment Life imprisonment Gun politics Executive President of Mexico Andrés Manuel López Obrador(MORENA) List of heads of state Federal government Cabinet Legislature Congress of the Union LXIII Legislature of the Mexican Congress Senate of the Republic President of the SenateAna Lilia Rivera (MORENA) Chamber of Deputies President of the ChamberMarcela Gu...

еЊЃеИЖжЦєз®ЛеЉПгГКгГУгВ®вАУгВєгГИгГЉгВѓгВєжЦєз®ЛеЉПгАВйЪЬеЃ≥зЙ©гБЃеС®еЫ≤гБЃж∞ЧжµБгБЃгВЈгГЯгГ•гГђгГЉгВЈгГІгГ≥гБЂзФ®гБДгВЙгВМгВЛгАВ зѓДеЫ≤ иЗ™зДґзІСе≠¶еЈ•е≠¶ 姩жЦЗе≠¶ зЙ©зРЖе≠¶ еМЦе≠¶ зФЯзЙ©е≠¶ еЬ∞и≥™е≠¶ ењЬзФ®жХ∞е≠¶ йА£зґЪдљУеКЫе≠¶ гВЂгВ™гВєзРЖиЂЦ еКЫе≠¶з≥ї з§ЊдЉЪзІСе≠¶ зµМжЄИе≠¶ еАЛдљУзЊ§еЛХжЕЛиЂЦ еИЖй°Ю гВњгВ§гГЧ еЄЄ еБП еЊЃеИЖдї£жХ∞пЉИиЛ±и™ЮзЙИпЉЙ з©НеИЖеЊЃеИЖ еИЖжХ∞йЪО зЈЪеЮЛ йЭЮзЈЪ嚥 е§ЙжХ∞гБЃгВњгВ§гГЧгБЂгВИгВК зЛђзЂЛе§ЙжХ∞гБ®еЊУе±Юе§ЙжХ∞пЉИиЛ±и™ЮзЙИпЉЙ иЗ™еЊЛеЊЃеИЖжЦєз®ЛеЉП и§Ззі† Cou...

гБУгБЃи®ШдЇЛгБѓи™ЮеП•гБЃеЖЕйГ®гГ™гГ≥гВѓгАБи¶ЛеЗЇгБЧгБЃгГЮгГЉгВѓгВҐгГГгГЧгБ™гБ©гВєгВњгВ§гГЂгГЮгГЛгГ•гВҐгГЂгБЂж≤њгБ£гБЯдњЃж≠£гБМењЕи¶БгБІгБЩгАВ гВ¶гВ£гВ≠гГЪгГЗгВ£гВҐгБЃдљУи£БгБЄгБЃдњЃж≠£гБЂгБФеНФеКЫгБПгБ†гБХгБДпЉИгГШгГЂгГЧпЉЙгАВпЉИ2020еєі1жЬИпЉЙ гВЄгГІгГЉгВЄгГїгГХгГЉгВЈгВІGeorge Fouche гВЄгГІгГЉгГАгГ≥F1гВТгГЖгВєгГИгБЩгВЛгГХгГЉгВЈгВІгАВ(1994еєі)еЯЇжЬђжГЕ冱еЫљз±Н еНЧгВҐгГХгГ™гВЂеЕ±еТМеЫљзФЯеєіжЬИжЧ• (1965-05-15) 1965еєі5жЬИ15жЧ•еЗЇиЇЂеЬ∞ еРМгГїгГЧгГђгГИгГ™гВҐж≠їж≤°жЧ• (2023-05-05) 2023еєі5жЬИ5пњљ...


